【Python的可视化分析】蒙特卡洛模拟（上）

数据信息化 2019-11-20

993

人们常说，赌博碰不得，老人们更是常言十赌九输。难道赌博面前人人非酋？就拿最普通的掷骰子来说，共六个面，不管赌大赌小赢的概率都是50%，那么赌的次数多了，难道就会输的倾家荡产？

接下来我们用一种模拟的的Python数据化方式来验证一下，输赢是否只是单纯的运气问题。

首先，我们来了解一个概念——

蒙特卡罗方法
https://zh.wiki.6bu6.xyz/wiki/蒙地卡羅方法

这个方法也被称为统计模拟方法，是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。

本次模拟为保证数据的准确性，均使用该方法来计算处理数据。

先到一个好玩的网址来感受下二维平面随机游走的魅力：http://itsof.me/qmas/deliverables/01-random_walk/

这里可以看到二维平面随机游走模拟实验：

Border limit 边界限制

Steps to take 要走的步数

Number of simulations 模拟次数

Animation delay in ms 动画延迟

我们分别设置参数为10，10，100，10可以看到：

类似北京以天安门为中心错综复杂的地铁

当然，本文的二维随机游走模拟是基于Python来开发的，下面让我们来看看Python是怎么处理的。

首先以坐标(0,0)为原点，步数限制为20来进行模拟随机游走过程，代码如下：

#二维随机游走方法一：
import random


def random_walk(n):
    x=0
    y=0
    for i in range(n):
        step=random.choice(['N','S','W','E'])
        if step == 'N':
            y+=1
        elif step == 'S':
            y-=1
        elif step == 'W':
            x-=1
        else:
            x+=1
    return(x,y)
    
for i in range(20):
    one_walk=random_walk(20)
    how_far=int(one_walk[0])**2+int(one_walk[1]**2)
    if how_far>=50:
        print(one_walk,'It is so far!')
    else:
        print(one_walk,'well')
    #print(one_walk,how_far)

打印随机结果发现随机走了20步只有小部分的坐标平方和大于等于50，显示It is so far!：

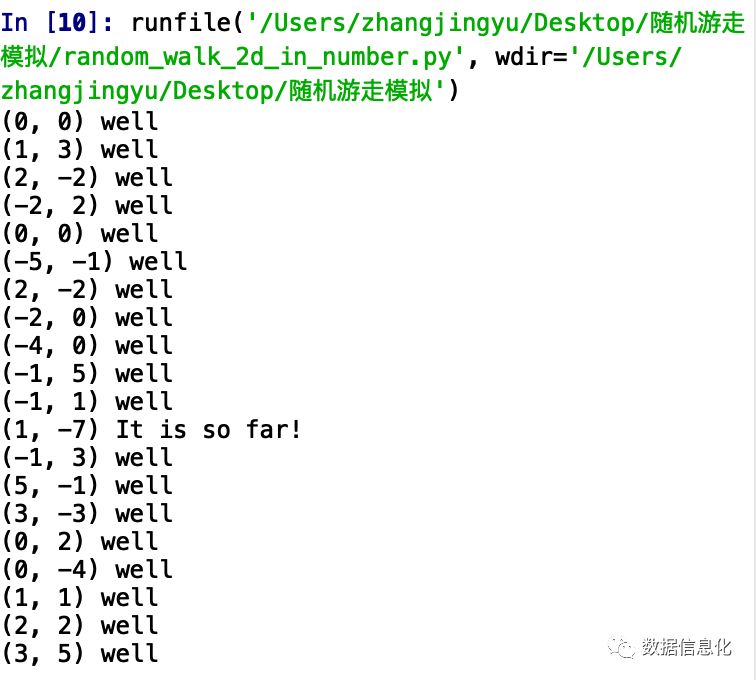
然后，我们对上述代码进行改良，简化下写法同时写出具体的行走路径长度，代码如下：

#二维随机游走方法二：
import random


def random_walk_V2(n):
    x,y=(0,0)
    for i in range(n):
        (dx,dy)=random.choice([(0,1),(0,-1),(-1,0),(1,0)])
        x+=dx
        y+=dy
        
    return(x,y)
    
for i in range(20):
    one_walk=random_walk_V2(20)
    print(one_walk,'距离坐标(0,0)的单位长度为：',abs(one_walk[0])+
          abs(one_walk[1]))

打印结果可以看到随机走的路径长度：

最后根据上述代码来计算出超过限制区域的占比，代码如下：

# 超过范围区域的占比：
import random


def random_walk_V2(n):
    x,y=(0,0)
    for i in range(n):
        (dx,dy)=random.choice([(0,1),(0,-1),(-1,0),(1,0)])
        x+=dx
        y+=dy
        
    return(x,y)


more_counter=0      #超过限制区域的计数
how_many_simulations=1000  #模拟运行次数
how_many_steps=200  #运行的步数
region_limit=100  #区域限制大小




for i in range(how_many_simulations):
    one_walk=random_walk_V2(how_many_steps)
    how_far=int(one_walk[0])**2+int(one_walk[1]**2)
    if how_far>=region_limit:
#        print(one_walk,'It is so far!')
        more_counter+=1
    else:
        pass
#        print(one_walk,'well')
        
#    print(one_walk,how_far)


print('$ of more outer:',more_counter/how_many_simulations)

最后可以看到随机结果占比大约在63%左右，通过改变模拟运行次数，这个数字会越来越精确，当模拟次数达到1万次时，数值会稳定在62.5%左右。如下：

同理，博弈的输赢不只光看运气，博弈的次数也占了很大的因素。下期我们将对博弈次数进行100，1000，10000次的模拟，同时进行matplotlib图像化展示数据。

下期：【Python的可视化分析】蒙特卡洛模拟（中）

python

文章转载自数据信息化，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。

【Python的可视化分析】蒙特卡洛模拟（上）

评论