递推的概念
递推算法:
是指从已知的初始条件出发,依据某种递推关系,逐次推出所要求的各中间结果及最后结果。
特点:
1、问题可以划分成多个状态;
2、除初始状态外,其它各个状态都可以用固定的递推关系式来表示。
首要问题:
得到相邻的数据项间的关系(即递推关系)。
一般来说,可以将递推算法看成是一种特殊的迭代算法。
递推的概念——递推关系式
给定一个数的序列H0,H1,…,Hn,…若存在整数n0,使当n>n0时,可以用符号(或大于号、小于号)将Hn与其前面的某些项Hi(0<i<n)联系起来,这样的式子就叫做递推关系式
递推关系式:Hn=Hn-1+Hn-2
递推的概念——斐波那契(Fibonacci)数列
Fibonacci数列的代表问题是由意大利著名数学家Fibonacci于1202年提出的“兔子繁殖问题”引出的
一对兔子,从出生满2月起,每个月都生一对兔子。小兔子长到第3个月后每个月又生一对兔子。假如兔子都不死,请问第1个月出生的一对兔子,第n个月有几只兔子?
问题分析:前提——不考虑兔子死亡
用小写字母表示新兔子,用大写字母表示具备生育能力的兔子
第1个月:放入一对新兔子r1。
第2个月:还是一对兔子,但已具备生育能力r1变成R1。
第3个月:R1生新兔子r2,兔子变为R1+r2。
第4个月:R1生新兔子r3,r2变R2。兔子为R1,R2,r3。
第5个月:R1和R2生新兔子r4和r5,r3变为R3。兔子为R1,R2,R3,r4,r5
…
递推的概念——斐波那契(Fibonacci)数列
Fibonacci数列递推方程:
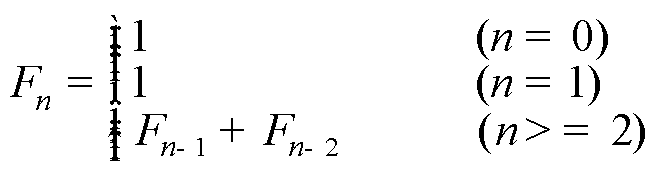
递推算法以初始(起点)值为基础,用相同的运算规律,逐次重复运算,直至运算结束。这种从“起点”重复相同的方法直至到达一定“边界”,犹如单向运动,用循环可以实现。递推的本质是按规律逐次推出(计算)先一步的结果
代码如下:
#include <iostream>
using namespace std;
int main(){
int a[1000],n;
cin>>n;
a[0]=a[1]=1;
for(int i=2; i<=n; i++){a[i]=a[i-1]+a[i-2];}
cout<<a[n];
return 0;}
什么是顺推和逆推
顺推法:从已知条件出发,逐步推出要解决的问题的结果。
逆推法:从问题结果出发,逐步推到已知条件。
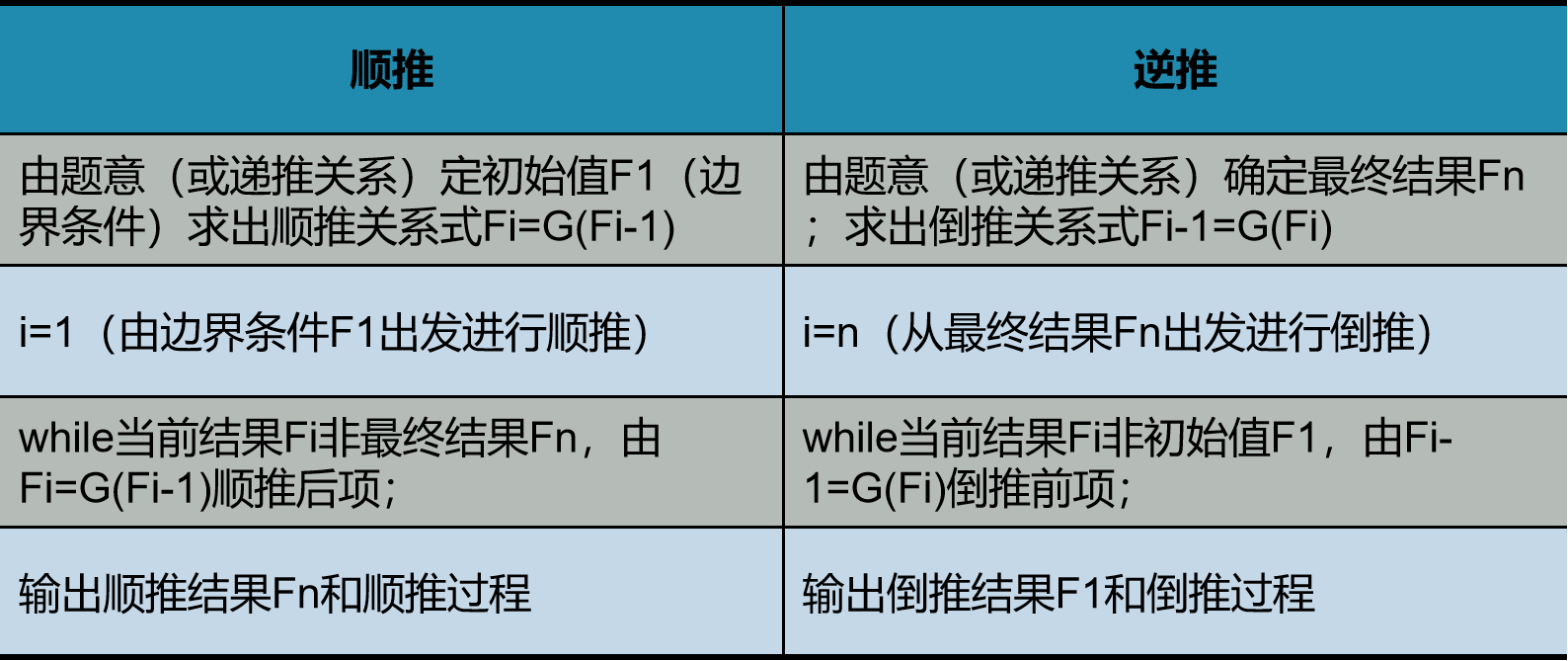
解决递推问题的一般步骤:
1、建立递推关系式;2、确定边界条件(即初始值);3、递推求解
顺推和逆推的应用——顺推
顺推(骨牌问题)
有2n的长方形方格,用n个12的骨牌铺满方格。编一程序,试对给出的任意一个n(n>0),输出铺法总数。
顺推和逆推的应用——顺推
推出一般规律:
对于一般的n,假设其铺法总数为xn
若第一个骨牌是竖排列放置时,剩下n-1个需要排列,其排列方法数刚好为xn-1
若第一个骨牌是横排放置时,则整个方格至少有2个骨牌横排,则剩下n-2个需要排列,排列方法为xn-2
顺推和逆推的应用——顺推
初始条件:或是问题本身已经给定,或是通过对问题的分析和化简后确定
代码如下:
#include <iostream>
using namespace std;
int main(){
int a[1000],n;
cin>>n;
a[1]=1; //初始化边界条件
a[2]=2;
//开始递推
for(int i=2; i<=n; i++){a[i]=a[i-1]+a[i-2];}
cout<<a[n]<<endl;
return 0;}
【题目描述】
科学家在热带森林中发现了一种特殊的昆虫,这种昆虫的繁殖能力很强。每对成虫过x个月产y对卵,每对卵要过两个月长成成虫。假设每个成虫不死,第一个月只有一对成虫,且卵长成成虫后的第一个月不产卵(过X个月产卵),问过Z个月以后,共有成虫多少对?
0≤x≤20, 1≤y≤20, x≤z≤50。
【输入】
x,y,z的数值。
【输出】
过z个月以后,共有成虫对数
【输入样例】
1 2 8
【输出样例】
37
问题分析:
本月成虫数量=上月成虫数量+两个月前新增卵的数量
新增卵的数量=上月成虫数量*Y
代码如下:
#include <iostream>
using namespace std;
int main(){
long long a[101]={0},b[101]={0};
int x,y,z;
cin>>x>>y>>z;
for(int i=1;i<=x; i++){
a[i]=1;
b[i]=0;}
for(int i=x+1; i<=z+1; i++){
b[i]=y*a[i-x];
a[i]=a[i-1]+b[i-2];}
cout<<a[z+1]<<endl;
return 0;}
顺推和逆推的应用——逆推
逆推(猴子分桃)
【问题描述】海滩上有一堆桃子,N只猴子来分。第一只猴子把这堆桃子中的一个扔入海中,然后将剩余的桃子平均分成两份,最后这只猴子拿走了1份。第二只猴子来了接着把剩下的桃子中的一个扔入海中,然后把剩余的桃子平均分成2份,开开心心拿走了1份。第三、第四、…,第N只猴子都是将剩下的桃子中的一个扔入海中,然后将剩余的桃子平均分成2份,并拿走其中的1份。最后只剩下1个桃子。编写程序,输入猴子的数量N,输出海滩上原有多少桃子。
过程分析:
a1=n; a2=(a1-1)/2; a3=(a2-1)/2……an-1=3, an=1
可得递推公式为:
an=(an-1-1)/2; (1)
即an-1=an*2+1; (2)
Tips-式(2)与式(1)比较:an已知,求a1,因此用递推算法时写成用an求前方项,同时此做法可减少整数除法带来的困扰,还可节省计算时间
代码如下:
#include <iostream>
using namespace std;
int main(){
int sum=0,n,a[1000]={};
cin>>n;
a[n]=1;
int i=n;
while(i>=0){
a[i-1]=a[i]*2+1;
i--;}
cout<<a[0]<<endl;
return 0;}
【问题描述】几名同学争做计算题,规定做完一道才能做第二道,比赛后统计发现: 第一位同学做了总数的一半多1道,第二位同学做了余下的一半多2道,第三位同学做了再余下的一半多3道,以此类推,第n-1位同学做了余下的一半多n-1题,最后一位同学做了n道。输入学生的数量n,求共有多少道题目?
int i=n;
while(i>=0){a[i-1]=(a[i]+i-1)*2; i--;}
cout<<a[0]<<endl;
return 0;}
五种典型的递推关系
Fibonacci数列-兔子繁殖问题
Hanoi塔问题
平面分割问题
Catalan数
第二类Stirling数
五种典型的递推关系——Hanoi塔问题
Hanoi塔问题
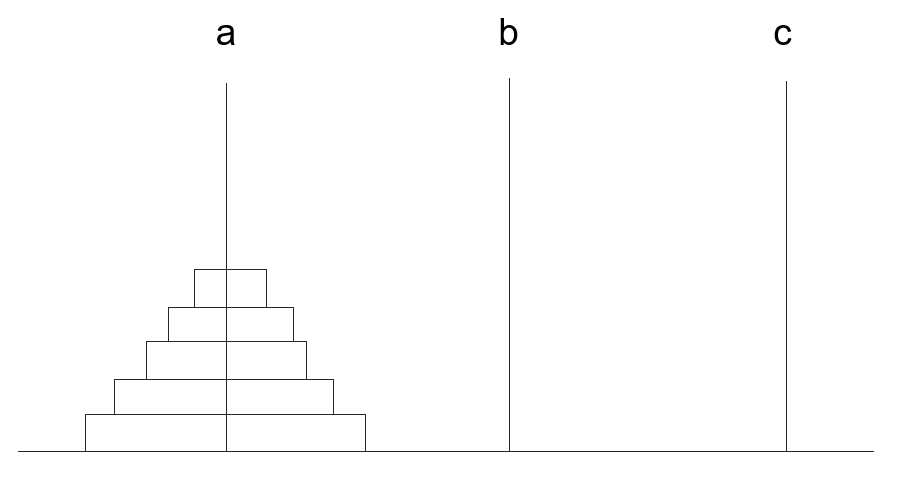
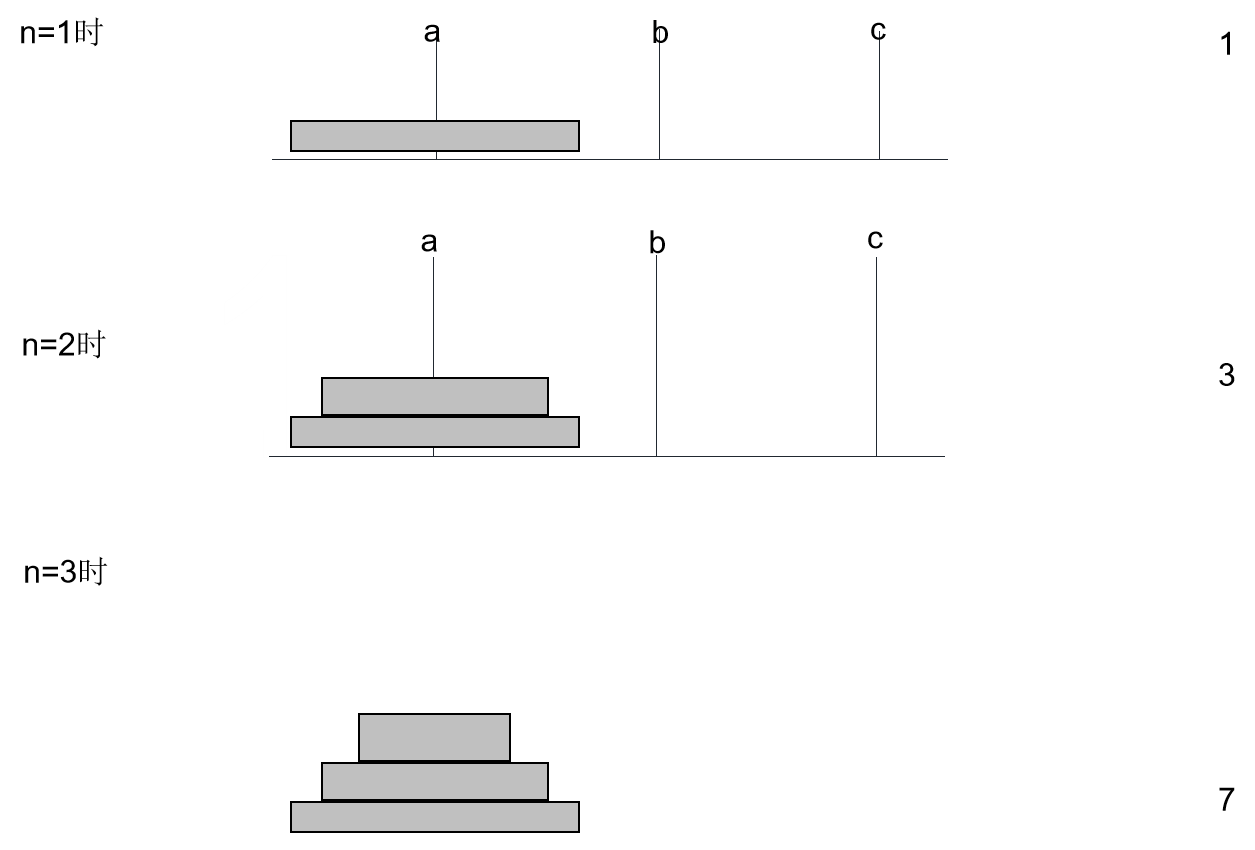
问题的提出:
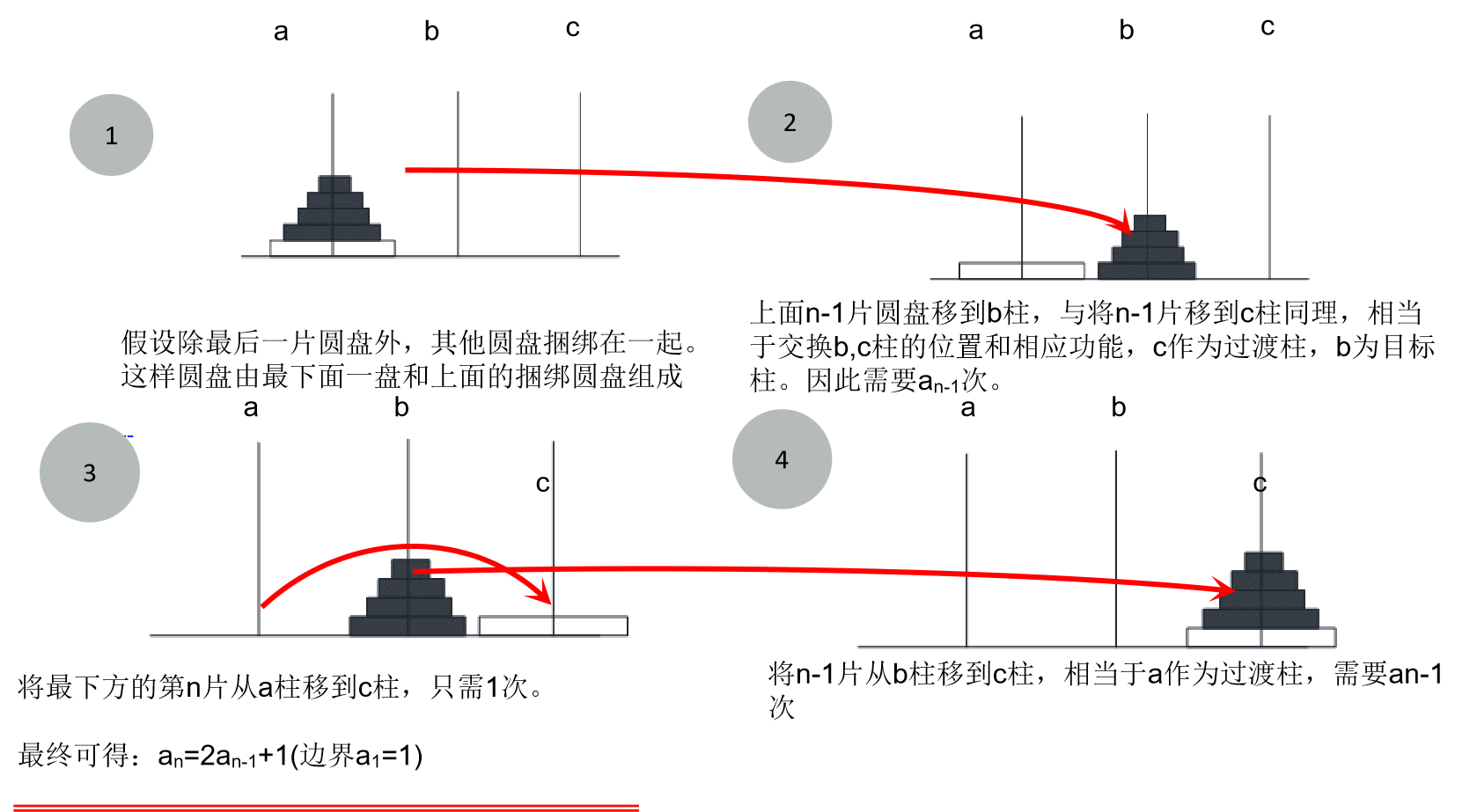
汉诺塔由编号为n个大小不同的圆盘和三根柱子a,b,c组成。开始时,这n个圆盘由大到小依次套在a柱上,如图所示。要求把a柱上n个圆盘按下述规则移到c柱上:
一次只能移一个圆盘,它必须位于某个柱子的顶部;
圆盘只能在三个柱上存放;
任何时刻不允许大盘压小盘。
问将这n个盘子从a柱移动到c柱上,最少需要移动多少次?
五种典型的递推关系——平面分割问题
问题的提出:
有n条封闭曲线画在平面上,而任何两条封闭曲线恰好相交于两点,且任何三条封闭曲线不相交于同一点,问这些封闭曲线把平面分割成的区域个数。
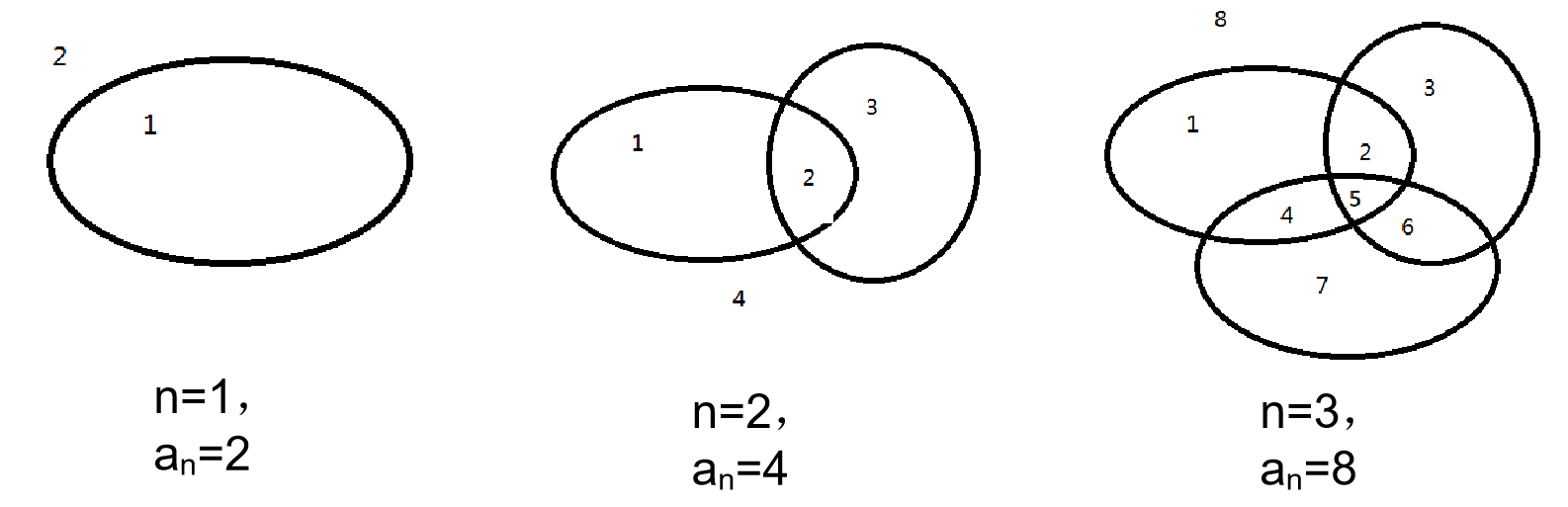
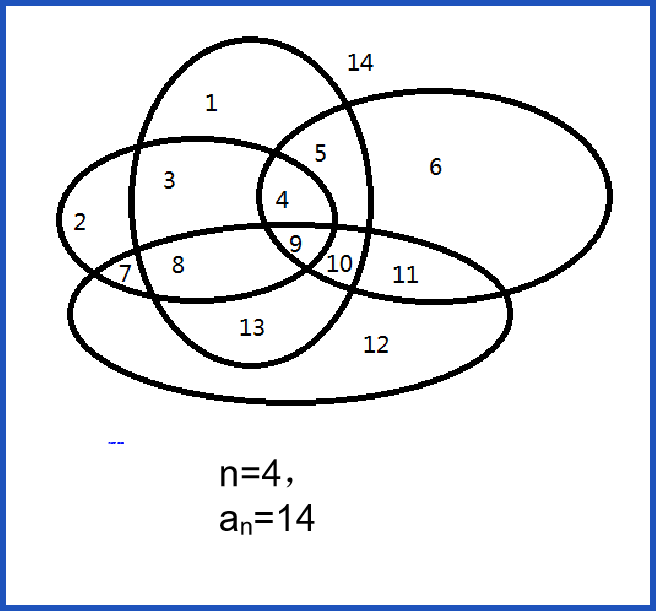
数学分析:
每当增加一个椭圆时,由于与之前的每个圆都相交于不同的两点,而两点间的圆弧就能构成新的区域,则每增加一个椭圆,原区域都被分割成两份。
存在规律:
an=an-1+2(n-1)
五种典型的递推关系——Catalan数
问题描述:一个凸n边形,通过不相交于n边形内部的对角线,把n边形拆分成若干三角形,不同的拆分数目用hn表示,hn即为Catalan数。例如五边形有如下五种拆分方案(如图),故h5=5。求对于一个任意的凸n边形相应的hn。 输入 一个正整数n,代表凸n边形的边数 (2≤n≤37) 输出 一个正整数,凸n边形划分成若干三角形的不同划分方式
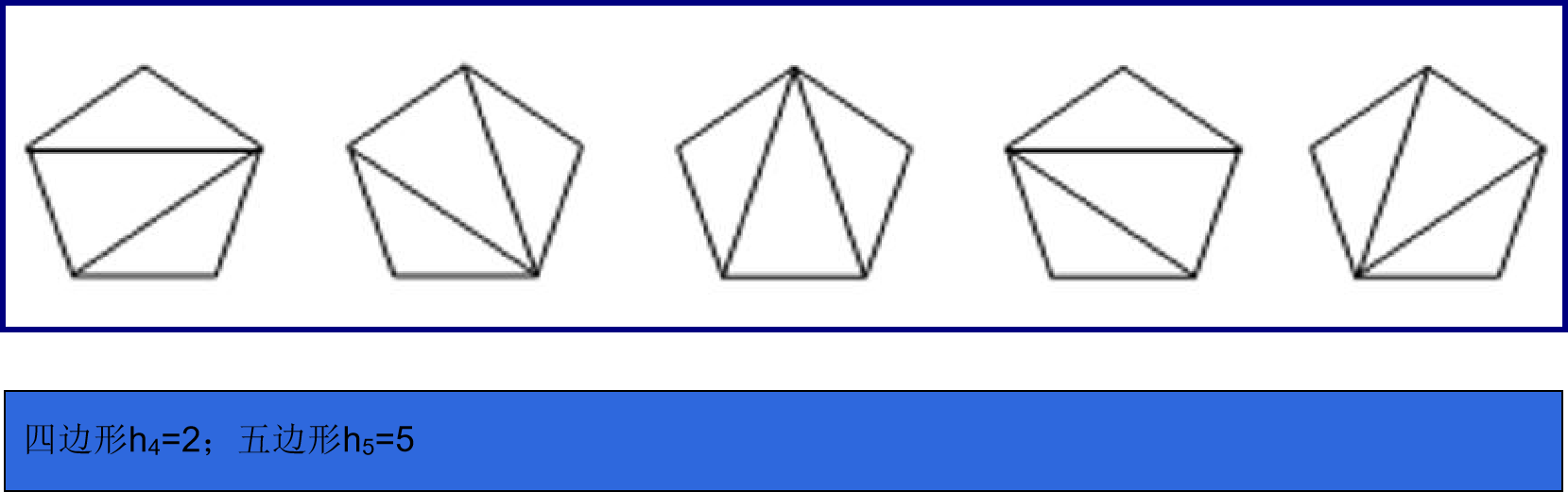
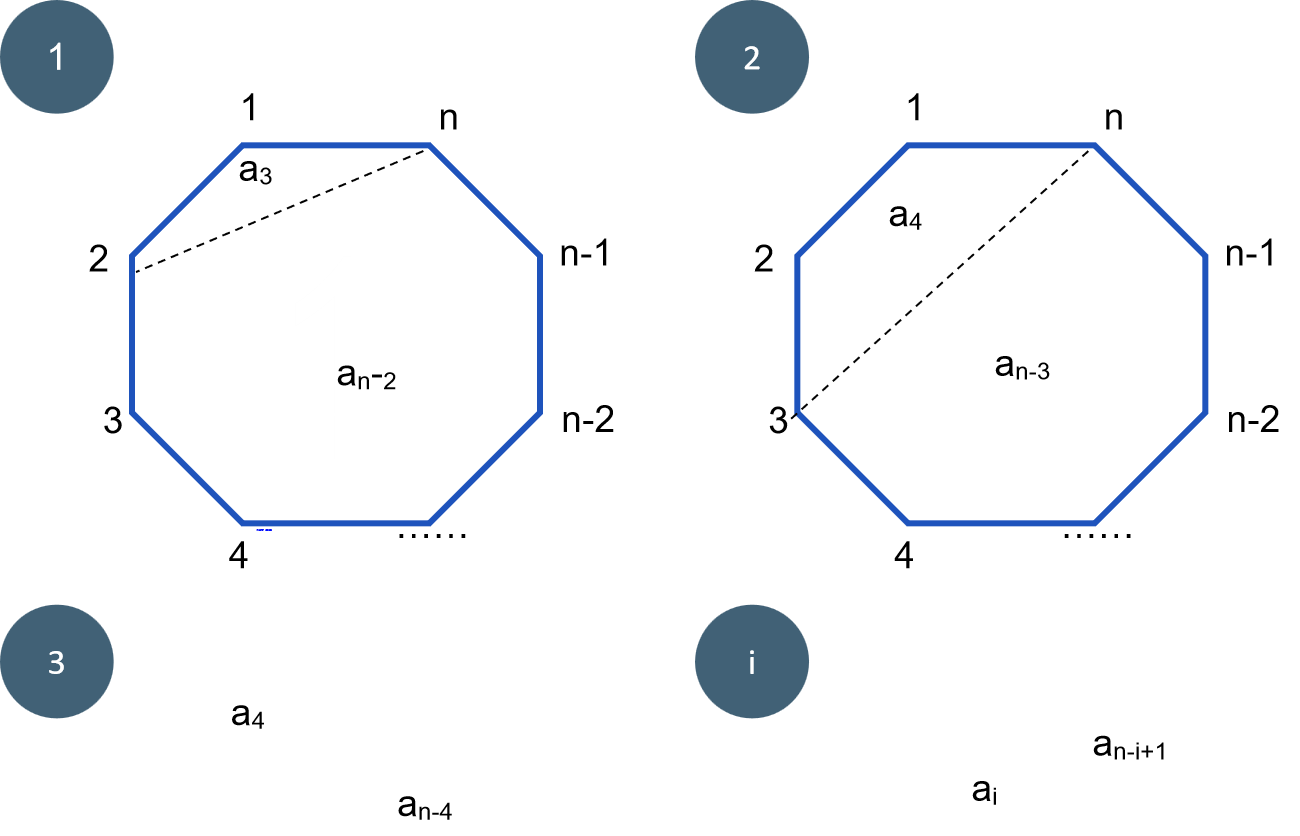
特点:凸n边形有n条边。
凸n边形的任意一条边都必然是一个三角形的一条边
当有n-1条边时,有an-1种三角形剖分办法
当增加一个顶点n时,可以有多种剖分办法将n边形分成另外两个多边形
这两多边形和为n+2.
an =a2 * an-1 + a3 * an-2+ a4 * an-3 + a4 * an-4 +……+ai * an-i+1+…
五种典型的递推关系——第二类Stirling数
定义:n个有区别的球放到m个相同的盒子中,要求无一空盒,其不同的方案用S(n,m)表示,称为第二类Stirling数
重点:盒子不能为空,当已经有n-1个球放入盒子中时。第n个球放入时只能有两种情况:
第n球独占一盒子时,前面n-1球只能放在m-1个盒子中,方案数为S(n-1,m-1)
第n球与其他球共占同一盒子时,其他n-1球放入m个盒子中,有S(n-1,m)种,而n可放入m个盒中的任意一种,即有mS(n-1,m)种
根据定义,边界条件:S(n, 0)=0; S(n, 1)=1;
S(n, n)=1; S(n, k)=0;
k>n
sn = S(n-1,m-1)+ mS(n-1,m)
n>1, m>=1






