文章只解释熵值的计算及代表意义:
简单理解就是熵值代表了数值的混乱程度,熵越小那么数据越规律
定义:
熵,热力学中表征物质状态的参量之一,用符号S表示,其物理意义是体系混乱程度的度量。在信息技术中,它就是指一个事情的不确定的程度.在信息技术中的计算式是(即该信息的不确定性)p是事件发生的概率
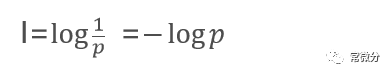
熵值,信源的平均不确定性,称为信息熵,二点分布x的信息熵用下面的公式表示:
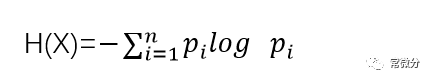
(ps:当式中的对数的底为2时,信息熵的单位为比特。底数为其它时,它对应的单位也不一样。logn(q)表示具有总概率q的那些最可能序列为了描述序列所需要的二进制位数 .信息熵是信息论中用于度量信息量的一个概念。一个系统越是有序,信息熵就越低;反之,一个系统越是混乱,信息熵就越高。所以,信息熵也可以说是系统有序化程度的一个度量。)
计算实例:
要计算熵值首先要先了解概率的分布定义。概率分布主要分为:二点分布,均匀分布,二项分布,泊松分布等。
我们以二点分布为例,
X取值分别为0和1, P为取值的概率,当X=1, P(X=1)=P ;当X=0 P(X=0)=1-P
如下表:

计算实例:(以底数为2计算单位为比特的信息熵,比特(bit)即意味着该系统的字节数衡量。以我们的二点分布为例)
例1:当p=0.5时,i=(0,1)
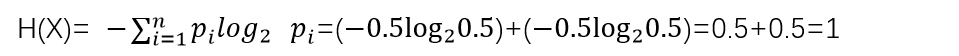
即可见信息的物理含义是通信编码所需要的比特数。结合上面的例子,X 有两种取值,用 1bit 就可以编码。与计算出的 信息 = 1 相吻合。
例2:当p=0 时,
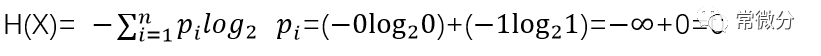
结果与确定事件熵为 0 相吻合。
例3:设X服从下述分布:

则熵计算为:
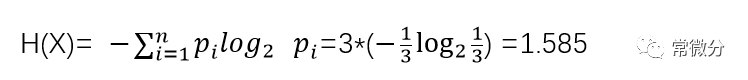
例 1 :两种情形的等概率事件,1 个bit位就可以编码,与计算的熵 =1吻合;
例 2 :确定事件无需编码,0 个bit位,与计算出的熵 = 0 吻合;
例 3 :三种情形的等概率事件,2 个bit位就可以编码,与计算出的熵 = 1.58 ≈ 2 也算吻合;(如果是四种情形的话就正好等于2!)






