如果说监督微调(SFT)是教大模型“背答案”,那么强化学习(RL)则是教它们“学方法”,在一次次试错与反思中自我进化。
2025年第三季度,RL在LLM领域迎来了新一轮突破性进展。研究重点已从简单应用转向了对RL本质的深度思考:这项技术是在开发新能力,还是在优化现有知识的提取效率?熵调控机制如何影响模型的学习极限?我们是否能够借助少量数据甚至无监督学习,推动模型实现自我迭代升级?
这篇盘点将带您潜入 Hugging Face 上 Q2 热度最高的RL论文:《Reflect, Retry, Reward: Self-Improving LLMs via Reinforcement Learning》,一窥当前最前沿的思想碰撞。让我们一起看看,强化学习究竟如何为大模型注入灵魂,重塑其能力的未来。
论文较长,分为上下两篇,本篇为下篇:

4
实验
我们通过两个不同任务的实验证明了我们方法的有效性:函数调用和数学方程。
4.1函数调用
我们使用APIGen数据集(Liu et al.,2024b)我们的函数调用实验。APIGen是60,000个高质量函数调用的数据集,包括用户查询(纯文本)、能够回答该查询的可能工具列表及其参数(JSON)以及具有正确参数和值的正确格式化的函数调用(JSON)。数据集中共有4211个唯一工具,平均每个工具有2.3个参数,每个用户查询平均有2.8个工具可供选择(最少1个,最多8个)。只有当一个模型不仅选择了正确的工具,而且生成了正确的参数和值,它才被认为是正确的。下面显示了一个有两种不同工具可供选择的样本数据点(格式更易于阅读)。
用户查询:
检查Vimeo用户名“john_doe_artist”是否可用。
提供的工具:
[{ "name": "vimeo ",
" description ":"使用检查给定的Vimeo用户名是否可用
→快速维修工具台。",
"参数":{ "用户名":{ "描述":"要检查的Vimeo用户名
→可用性。"," type": "str "," default": "username"}}
},
{ " name ":" get _ user _ pin ",
" description ":"检索指定用户的Pinterest pins。","参数":{ "用户名":{ "描述":" Pinterest用户名
→待取。"," type": "str "," default": "0869178429hau"}}
}]
正确答案:
[{"name": "vimeo "," arguments ":{ " username ":" John _ doe _ artist " } }]
为了保持我们实验的完整性,我们只评估在APIGen数据集发布(2024年6月)之前发布的模型。这确保了这些模型中的任何一个都不可能在数据集上被训练以获得不公平的优势。具体来说,我们报告Qwen2 (1.5B/7B指令)的结果(Yang et al.,2024),Llama3.1 (8B指令)(Grattafiori et al.,2024),和Phi3.5-mini指令(Abdin et al.,2024).我们还报告了Qwen2-72B Instruct、Llama3.1-70B Instruct和笔者的Palmyra X4的一般性能(Writer.com,2024)作为基线。
由于不同的模型系列也有不同的建议工具调用方法,我们为每个模型系列测试了不同的模板,并最终选择了提供最强基线的提示格式。对于我们的函数调用验证器,我们要求模型输出与数据集中的正确答案完全匹配(即基于基本事实标签)。我们使用以下提示为失败的函数调用尝试生成自我反映:
您尝试执行任务,但未能生成正确的工具调用。
→反思哪里出了问题,写一个对你有帮助的简短解释
→下次做得更好。
4.2倒计时数学方程式
我们使用TinyZero项目引入的倒计时数据集进行数学方程实验(Pan et al.,2025a,b).倒计时数据集由45万个3-4个数字的列表和一个目标数字组成。目标是将基本的算术运算应用于这些数字,从而使等式计算出目标数字。只有当一个模型使用所有的数字一次(以任何顺序)并且最终的等式成功地评估到目标数字时,它才被认为是正确的。下面显示了一个样本数据点。
使用数字[4,73,4,23],创建一个等于76的等式。可以用'→基本算术运算(+、-、*、/),每个数只能用'→一次。
与函数调用一样,为了保持我们实验的完整性,我们只评估在倒计时数据集公开(2025年1月)之前发布或知识中断的模型。具体来说,我们报告Qwen2.5 (1.5B/3B/7B指令)的结果(Yang et al.,2025),Llama3.1 (8B指令)、Llama3.2 (3B指令)和Writer的Palmyra 1.7B。我们还报告了Qwen2.5-32B指令、Qwen2.5-72B指令、Llama3.1-70B指令和Writer的Palmyra X4的一般性能(Writer.com,2024)作为基线。
我们再次为每个型号系列尝试了几种不同的提示格式,最终选择使用提供最强基线的格式。对于我们的数学方程验证器,我们要求生成的方程与提示中的目标答案相匹配(即不需要基本事实标签)。我们使用以下提示为失败的倒计时数学方程式生成自我反思:
你试图解决这个问题,但得到了错误的答案。反思哪里出了问题
→写一个简短的解释,帮助你下次做得更好。
4.3失败的数据集
出于效率的原因,为了便于更直观的分析,我们没有在完整的函数调用和数学方程训练集上训练我们的模型,而是选择首先为每个任务创建一个失败数据集。更具体地说,我们提示每个任务的每个模型为每个用户查询生成多达64个响应(取决于模型大小),并且只保留那些模型失败的查询(基于每个任务相关的验证器)。我们通常会为较大的模型生成更多的响应,因为它们比较小的模型失败的频率低,因此会产生较少的训练样本。为了加快剔除采样过程,我们使用了vLLM(Kwon et al.,2023)带前缀缓存。
这种方法有几个优点。首先,它节省了时间,因为没有必要在已经成功处理的查询上训练我们的自反射模型,因此不能从中学习。第二,通过为每个查询生成几个响应,我们使数据更加健壮;例如,如果一个基础模型在80%的时间里对同一个查询产生正确的响应,我们仍然可以从剩下的20%中学习,因为响应是不确定的。最后,通过在我们的数据集中只有失败案例,我们可以精确地确定模型在收敛到最佳自反射之前需要训练多少个样本。
我们必须强调,我们采取这种方法纯粹是出于效率和分析的原因,在其他方面,它在功能上等同于从现实世界的场景中学习,在这种场景中,我们接收到成功和失败的响应。
4.4多步GRPO
我们使用了TRL框架(von Werra et al.,2020)作为实现我们的多步GRPO算法的开始基础(即,从自我反思后的第二次尝试中学习)。特别是,我们扩展了GRPOTrainer并修改了它的_prepare_inputs函数,以调用second_step函数,该函数在给定GRPOTrainer生成的完成的情况下,将执行另一个完成生成步骤,而不会影响GRPOTrainer已经计算的掩码。当我们对失败的数据集进行操作,促使模型生成它的自我反思注释时,掩码对应于自我反思文本的标记。这样,我们可以根据需要对初始完成执行尽可能多的二级步骤,并且只奖励与初始完成相对应的令牌(通过GRPOTrainer生成的掩码)。second_step函数还添加了
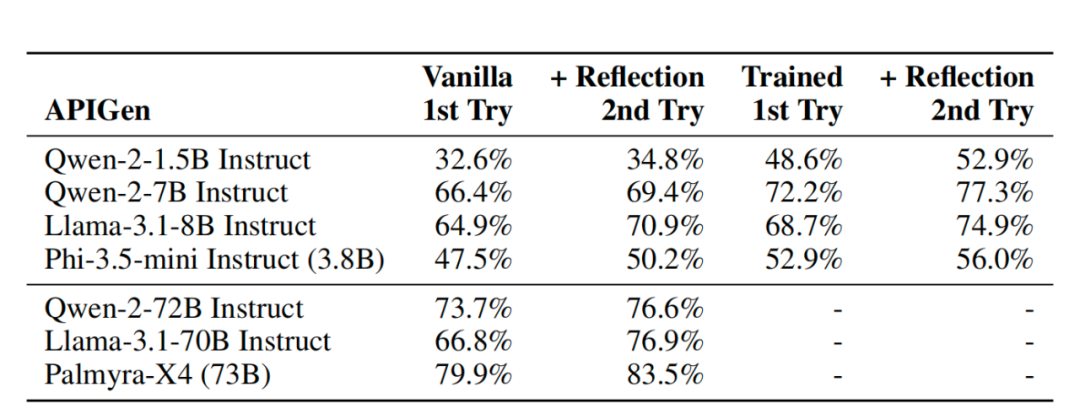
Table 1: APIGen结果该表显示了在第一次和第二次尝试中,以及在有/没有我们的GRPO自我反思训练的情况下,在我们的APIGen测试集(12,000个样本)上的准确度方面的模型性能。APIGen
发送到奖励函数的输入的数据结构,有助于理解连续步骤中初始完成的性能。这种多步骤的方法允许我们整合任何复杂的下游奖励机制,而不仅仅是奖励最初的完成。
我们在各自的故障数据集上训练了我们的模型,最多1,750步,有效批量为256次故障(尽管实际上大多数模型收敛得更快),我们在它们的收敛点对它们进行了评估。例如,在Llama-3.1-8B上进行的函数调用实验只需要100个训练步骤,并且使用了不到2000个唯一查询。只有一个函数调用实验看到了48,000个查询的整个数据集;所有函数调用实验的平均值小于25,000个唯一查询。任何数学方程式写作实验最多使用不到25,000个独特的问题;所有数学方程式写作实验的平均水平约为15,000个独特的问题。
我们使用原始DeepSeek实现中描述的标准GRPO训练参数(Shao et al.,2024),并进行了一些超参数实验。在我们的最终实验中,我们将KL发散系数设置为0.001,并使用5e-7的学习速率,余弦退火时间表和0.03的预热比。为了训练每个模型,我们使用了4到8个H100 GPUs。由于已知的计算效率和GRPO的可扩展性问题,我们将我们的实验限制在15亿到80亿个参数之间的模型(Zhang and Zuo,2025).
除了这里报告的实验结果之外,我们还用一些较小的模型进行了实验。然而,我们很快发现,这些模型在准确回答和自我反思方面的能力非常有限;例如Qwen2/Qwen2.5 0.5B指令和Llama3.2-1B指令。类似地,虽然微软的Phi 3.5 mini模型能够处理函数调用,但它在方程编写方面有很大的困难。我们不报告这些模型的结果。
5
实验结果
我们的主要实验结果显示在Table 1和Table 2.具体来说,Table 1显示了每个模型在多步GRPO训练前后在APIGen测试集(12,000个样本)上的第一次和第二次尝试的模型性能,同时Table 2显示了相同的情况,但用于倒计时测试集(15,000个样本)。
就APIGen而言,我们首先注意到,在一次尝试之后,模型大小与模型性能完美相关(如预期的那样)。我们还注意到,在第二次尝试使用自我反思后,性能平均提高了4.5%,这也与之前的工作一致。然而,在我们的GRPO培训后,我们看到了最大的增长,尽管我们只奖励自我反思令牌,但几乎所有的模型都能够在一次尝试后超越甚至两次尝试的普通模型。我们假设这是因为自反射标记通常有助于模型推理,因此即使模型不需要生成显式的自反射,它也会受益。尽管如此,在我们的培训之后,自我反思仍然有所帮助,当模型能够在第二次尝试中自我反思时,性能会进一步提高4.7%(平均)。最引人注目的是,我们观察到我们的Qwen-2-7B模型在GRPO训练后能够在两个模型都尝试两次时胜过普通的Qwen-2-72B模型,即使后者比前者大10倍。
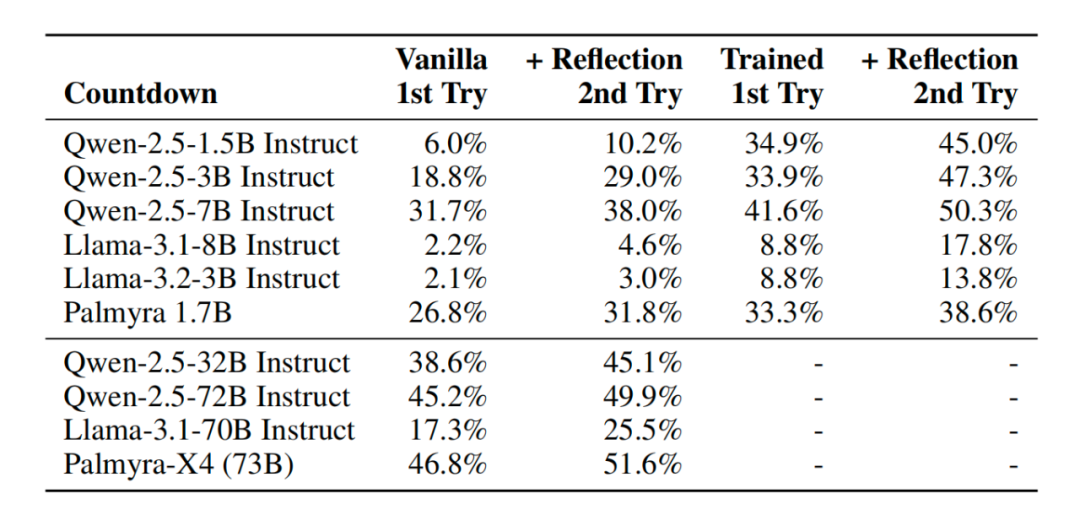
Table 2:倒计时结果该表显示了在第一次和第二次尝试中,以及在有/没有我们的GRPO自我反思训练的情况下,在倒计时测试集(15,000个样本)上,模型在准确性方面的表现。Countdown Results
从任务特定到可推广的自我反思

图2:更好的自我反思我们观察到,普通模型生成的反思往往很长,令人困惑,而且多余,而GRPO微调模型生成的反思要短得多,更清晰,也更具概括性。Better
在倒计时方面,首先值得注意的是,性能普遍较低,特别是香草美洲驼模型(美洲驼-3.1和美洲驼-3.2)确实很难完成任务;例如,美洲驼-3.1.70B型号甚至比小20倍以上的Qwen-2.5-3B型号还要厉害。在其他方面,改进的模式与APIGen实验类似,尽管幅度略高:在我们的GRPO训练前后,自我反思分别使表现平均提高了5.3%和8.6%。我们假设这些较大的收益来自于模型从较低的基线开始,因此有更大的学习机会。
最终,我们的发现不仅加强了之前关于自我反省的好处的工作,还证明了学习如何利用GRPO优化自我反省可以进一步提高绩效。
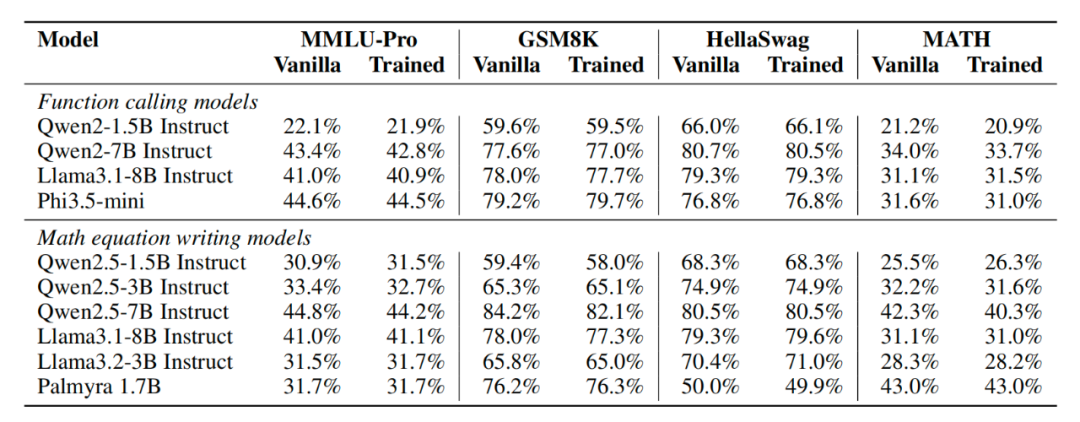
表3:灾难性遗忘分析普通和GRPO微调模型在普通LLM基准上的比较表明,尽管进行了微调,我们观察到最小的灾难性遗忘,微调模型在这些标准基准上保持了很强的性能。Catastrophic Forgetting Analysis
5.1更好的自我反省
为了深入了解自我反思训练后自我反思是如何提高的,我们提供了一个定性的例子,一个由普通模型产生的自我反思,以及由同一模型在GRPO训练后产生的自我反思Figure 2.显而易见,与训练后更简洁、优化的自我反思相比,普通的自我反思更长、更冗长、更重复。虽然这在直觉上是有道理的——人类同样更喜欢简短的指令——但这一发现与思维链风格的输出形成了对比,后者被认为表现更好,因为它们更冗长。对于什么时候生成简洁的输出比生成冗长的输出对一个模型更有利,我们把它作为一个开放的问题。
5.2低灾难性遗忘
微调模型时的一个常见问题是灾难性遗忘,即当模型学会专注于一项任务而牺牲其他任务时(Li and Hoiem,2016;Lopez-Paz and Ranzato,2017;Kotha et al.,2024).由于我们的自我反思训练旨在以与任务无关的方式提高性能,因此我们在几个不同的基准(MMLU-Pro)上评估我们的模型(Wanget al.,2024),GSM8K(Cobbe et al.,2021),海拉斯沃格(Zellers et al.,2019),和数学(Hendryckset al.,2021))为了评估他们在自我反思训练前后的语言理解、数学问题解决和常识推理能力。我们使用通用评估基准框架lm-eval来实现这一点(Gao et al.,2024).我们的假设是性能应该保持相对不变,因为我们从不针对特定任务进行优化,而是在总体上优化自我反思推理。
我们在中展示了我们的结果Table 3,并发现自我感染训练后表现确实保持稳定。在大多数情况下,与基本型号相比,性能下降不到1%,有些型号甚至有所改善;例如Qwen-2.5-1.5B在倒计时数据集上进行自反射训练后,在MMLU-Pro和MATH上的性能分别提高了0.6%和0.8%。我们将此视为我们的方法对灾难性遗忘具有鲁棒性的证据。
6
结论
在本文中,我们已经表明,通过训练一个模型来改进自我反思而不是特定任务,可以显著提高LLM的性能。这种间接方法只依赖于一个验证器,该验证器可以检测模型响应是正确的还是不正确的,因此特别适合于可以轻松验证响应的任务;例如,JSON输出的格式是否正确,生成的代码是否实际可执行,或者是否满足等式的所有约束。
我们通过在APIGen函数调用和倒计时数学方程求解数据集上的实验证明了我们方法的有效性,并发现使用GRPO进行自我反思训练的模型在函数调用测试集(12,000个样本)上平均提高了9.0%,在倒计时匹配方程数据集(15,000个样本)上平均提高了16.0%。我们进一步发现,尽管规模不同,但经过自我反思训练的较小模型在两项任务中的表现都优于未经训练的较大模型;例如,Qwen-2-7B指令(经过训练)在函数调用方面优于Qwen2-72B指令(未经训练),Qwen2.5-7B指令(经过训练)在倒数数学方程式方面优于Qwen2.5- 72B指令(未经训练)。我们的模型对灾难性遗忘也很稳健。
尽管我们只训练模型来提高自我反思能力,但我们发现即使在不需要自我反思的时候,它们的表现也明显更好;也就是说,他们第一次尝试就成功了,因此没有必要反思和再次尝试。我们假设这是因为通过关注自我反思而不是特定任务,模型可能更普遍地提高了他们的推理技能。在未来的工作中,我们希望调查自我反思训练是否适用于不同的任务。
7
限制
为每个任务定义一个二进制成功/失败验证器可能并不总是那么简单。我们开发我们的方法时考虑到带标签的训练数据可能很少,但我们认识到,如果可用的话,基本事实标签可以用作验证器。或者,也可以使用更大的模型作为判断(Zheng et al.,2023).
我们还发现我们的方法并不适用于所有模型和所有任务;该模型必须具备一些执行任务、自我反思和学习的基本能力,以便提高自我纠正能力。例如,Llama3.2-3B指令无法在函数调用任务中学会自我纠正。
内容来源:
https://huggingface.co/papers/2505.24726
(机翻)






