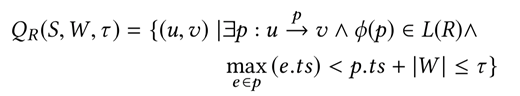本文将介绍解决regular path query(RPQ)相关问题的四种算法。ϕ(p)指的是path p的label串,L(R)指的是正则表达式R的正则语言。RPQ问题给定一个数据图和一个正则表达式R,想要找到这个数据图上满足ϕ(p)∈L(R) 的路径p。四个算法给出的输出不完全相同:有时,我们只需要给出这个路径的起点和终点;有时要给出整个路径;或者只需要在给定起点终点时返回这两个点之间是否存在满足ϕ(p)∈L(R) 的路径。Algorithms | Query类型 | 解 |
Rare label | RPQ | 所有路径 |
Landmark index | LCR | 给定起点和终点, 返回 True/False |
Random walk | RPQ | 给定起点和终点, 返回True/False with false negative |
Spanning tree | Streaming RPQ | 预先给定RE;返回所有满足条件的(起点,终点)点对 |
(André Koschmieder and Ulf Leser. 2012. Regular Path Queries on Large Graphs. In Proc. SSDBM 2012. 177–194. )这篇文章采用从rare label出发双向搜索的方式求得图中满足RPQ的所有路径。如果一个label一定会出现在RPQ的解路径中,即在RPQ的正则表达式中,这个label后面没有跟着 *、?这样的符号,那么我们说这个label是mandatory的。如果一个label是mandatory的,且它在数据图中出现至多m次,那么这个label是rare label。找到data graph中所有的rare label
在RPQ的第一第二、第二第三,…个rare label之间双向BFS搜索,找到它们之间的所有path
从第一个和最后一个rare label分别向后、向前搜索,使得path的label能连成一个完整的满足正则表达式的字符串。
从rare label出发搜索,能有效减小搜索空间,提高效率。算法2 基于Landmark index(LI)的算法 (LucienD.J. Valstar, George H.L. Fletcher, and Yuichi Yoshida. 2017. Landmark Indexingfor Evaluation of Label-Constrained Reachability Queries. In Proc. SIGMOD ’17.)这篇文章提出了基于Landmark index算法,解决Label-Constrained Reachability(LCR)问题。LCR问题给出起点和终点点对(s,t)以及一个label的集合,想得到“能否通过所有label都在集合中的path从s走到t”。LCR问题是RPQ的子集,相当于正则表达式形式为(a|b|c|…|n)*的RPQ。LI算法选取度数(入度和出度之和)最大的k个顶点作为landmark(algorithm 1)。在每个landmark vertex s上构建索引Ind(s)。索引Ind(s)满足:(v, L)在Ind(s)中当且仅当L是连接s和v的最小label集合(algorithm 2)。给定一个查询(s, t, L),我们从s开始执行考虑label的BFS搜索来寻找landmark vertex,之后从landmark vertex的索引中获得问题的解(algorithm 3)。(Sarisht Wadhwa, Anagh Prasad, Sayan Ranu,Amitabha Bagchi, and Srikanta Bedathur. 2019. Efficiently Answering RegularSimple Path Queries on Large Labeled Networks. In Proc. SIGMOD '19)这个算法解决的问题是,给定起点和终点(s, t),想得到“是否存在从s到t的满足RPQ的路径”。这个算法给出的是一个有假阴性的解。算法从s和t出发,进行双向的随机游走。选择下一跳邻居的要求是,跳到下一个之后,path依然是simple的,同时path的label串要能匹配上正则表达式的前缀(这样,继续往下游走才可能匹配上整个正则表达式)。没有合法的下一跳
游走达到了最大步数
前向和后向的随机游走遇上了,连起来之后得到了满足RPQ的解(return true)。
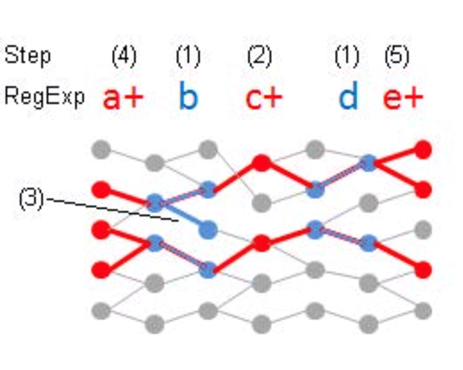
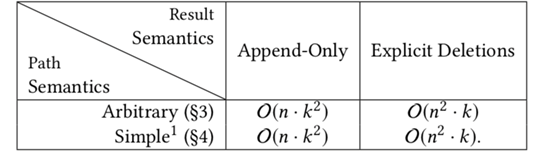
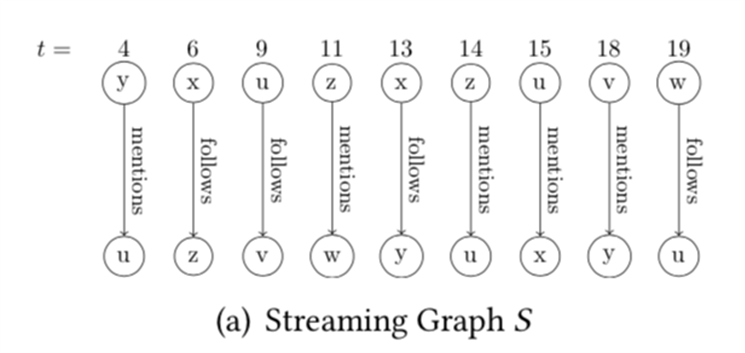
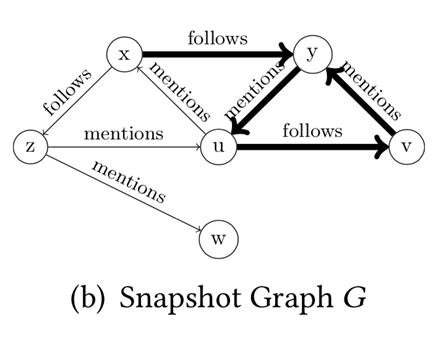
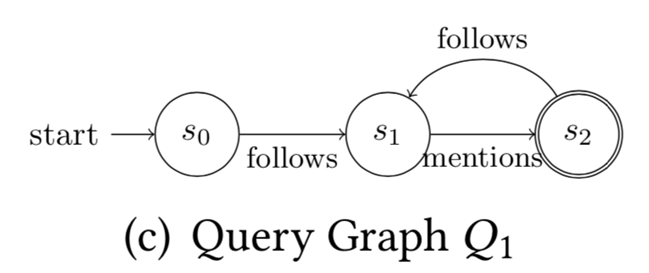
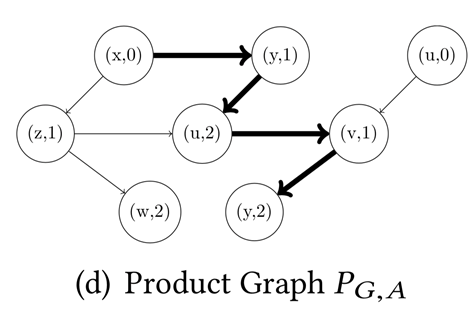
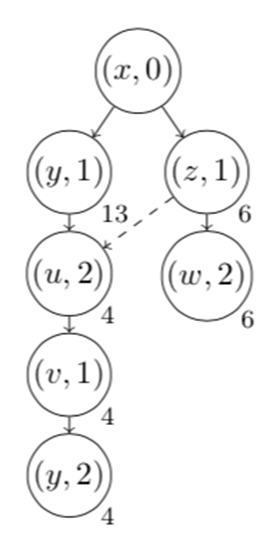
我们进行若干次这样的双向随机游走,就能得到一个有假阴性率的解决RPQ问题的算法。(Anil Pacaci, Angela Bonifati, and M. Tamer Özsu.2020. Regular Path Query Evaluation on Streaming Graphs. In Proceedings of the2020 ACM SIGMOD International Conference on Management of Data (SIGMOD '20).Association for Computing Machinery, New York, NY, USA, 1415–1430.)这个算法解决的是流图上的RPQ问题。Streaming RPQ的解就是在流图的snapshot graph上做RPQ得到的解。形式化定义如下:具体而言,文章对4类问题提出了算法。Path semantics指的是这个问题的解需要是simple path或者不需要;resultsemantics指的是是否需要支持显式删除。算法的核心思路是,通过用spanning tree记录历史的对于流图的snapshot graph和DFA的product graph的DFS,实现增量的RPQ算法。如下图,分别为图流、图流的snapshot graph、正则表达式R对应的DFA、snapshot和DFA的productgraph、spanning tree。Arbitrary & append-only的算法如下:Arbitrary &支持显式删除的算法如下,删除整个子树,并在spanning tree中补上之前剪枝的DFS搜索。对于simple path semantics,因为我们要保证path中没有重复的节点,访问到节点的路径会影响这个节点的后续搜索,所以我们在DFS时遇到已经访问过的节点不能停止搜索。
我们希望能找到满足某些性质的节点,使得重复访问这些节点时,可以剪枝,不继续搜索。我们把这类节点的集合记作Mx。
为了说明白Mx中的节点要具有什么性质,我们要先引入几个概念:
Suffix language: DFA上,把状态s送到F中的字符串的集合
Vertex v上有conflict:在product graph P上有一条以(x,0)为起点的路径,依次访问了(v , t’) 和(v, t) ,但[t’] ⊉ [t].
Conflict predecessor: 在spanning tree中,从根节点(x,0)出发的路径依次访问两个节点(v,s)(v,t),且(v,s)是路径上第一个vertex参数为v的节点,如果(v,s)(v,t)之间有conflict, 那么这条路径上它们之间的所有节点都称作conflict predecessor。
Mx中节点的性质:以Mx中节点为根的子树中不存在conflict predecessor。
如上所述,处理simple path的streaming RPQ的算法如下:




实验分析:

上图中展示了用于试验的11类query。其中,Q3, Q6中有多个Kleene star,Q4, Q9中有在多个或关系的符号上的Kleene star。环对于query运行时间的影响很大,因此这四个query会比其他query慢。Q11没有Kleene star,因此会比较快,spanning tree占用的内存也比较小。
下图figure 3 和4显示了不同query在不同数据集上的运行速度,以及stackoverflow上spanning tree的大小。
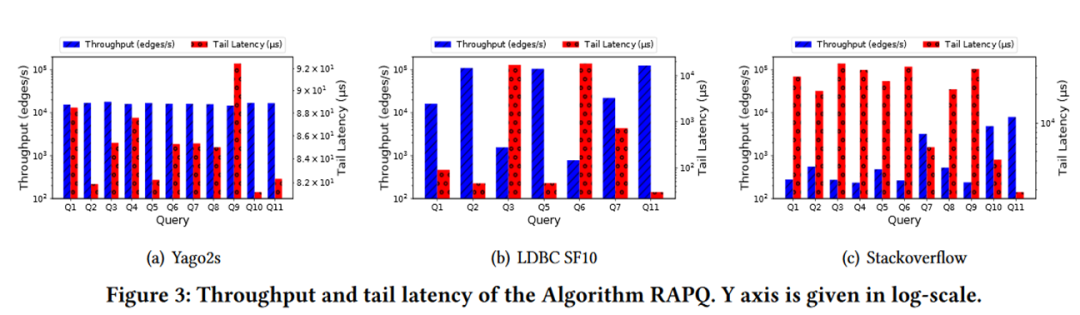
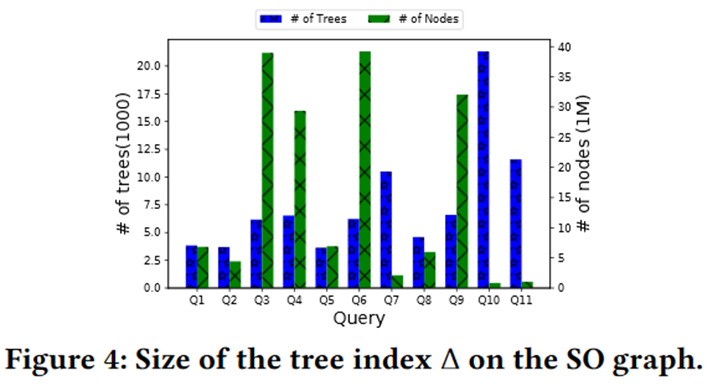
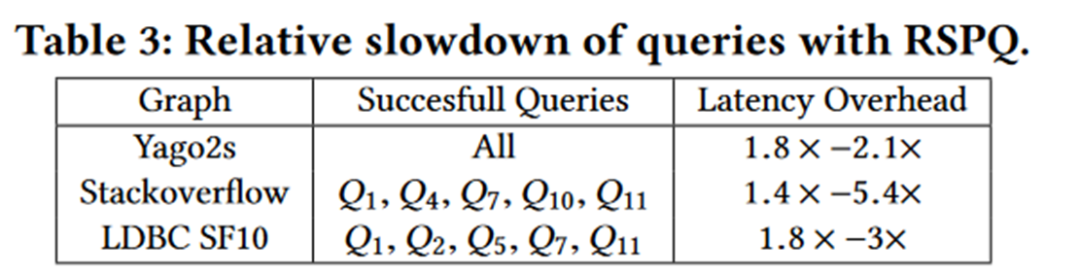
Table 3 显示了不同数据集上simplepath比arbitrary path额外的开销。开销主要来自于conflict的检测,以及对是否属于Mx的标记的维护。Yago2s中没有conflict,Q1、Q4、Q11都是conflict-free的,所以比较快;SO是highly cyclic的,所以比较慢。
参考文献:
André Koschmieder and Ulf Leser. 2012. RegularPath Queries on Large Graphs. In Proc. SSDBM 2012. 177–194.
Lucien D.J. Valstar, George H.L. Fletcher, andYuichi Yoshida. 2017. Landmark Indexing for Evaluation of Label-ConstrainedReachability Queries. In Proc. SIGMOD ’17.
Sarisht Wadhwa, Anagh Prasad, Sayan Ranu, AmitabhaBagchi, and Srikanta Bedathur. 2019. Efficiently Answering Regular Simple PathQueries on Large Labeled Networks. In Proc. SIGMOD '19
Anil Pacaci, Angela Bonifati, and M. Tamer Özsu.2020. Regular Path Query Evaluation on Streaming Graphs. In Proceedings of the2020 ACM SIGMOD International Conference on Management of Data (SIGMOD '20).Association for Computing Machinery, New York, NY, USA, 1415–1430.