红客突击队

算法系列:最短路径问题详解—Dijkstra算法、Floyd-Warshall算法、Bellman-Ford算法（SPFA算法）

前言

本篇归纳最短路径问题
即寻找从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径
主要有三种算法

• Dijkstra算法

• Floyd-Warshall算法

• Bellman-Ford算法（SPFA算法）

1、Dijkstra算法

Dijkstra算法本质是个贪心排序
以起始点为中心向外层层扩展，直到扩展到终点为止
不适用于带负权的图（要用Floyd算法）
时间复杂度是O(N² + E)，空间复杂度是O(N+E).

思路很简单：

• 指定起点s，引入集合S记录已求出最短路径的顶点(以及相应的最短路径长度)，和U记录还未求出最短路径的顶点(以及该顶点到起点s的距离)

• 初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为"起点s到该顶点的距离"（例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为无穷）

• 从U中选出"距离最短的顶点k"，并将顶点k加入到S中；同时，从U中移除顶点k

• 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。

• 重复步骤(2)和(3)，直到遍历完所有顶点。

下面看个图例以更好理解


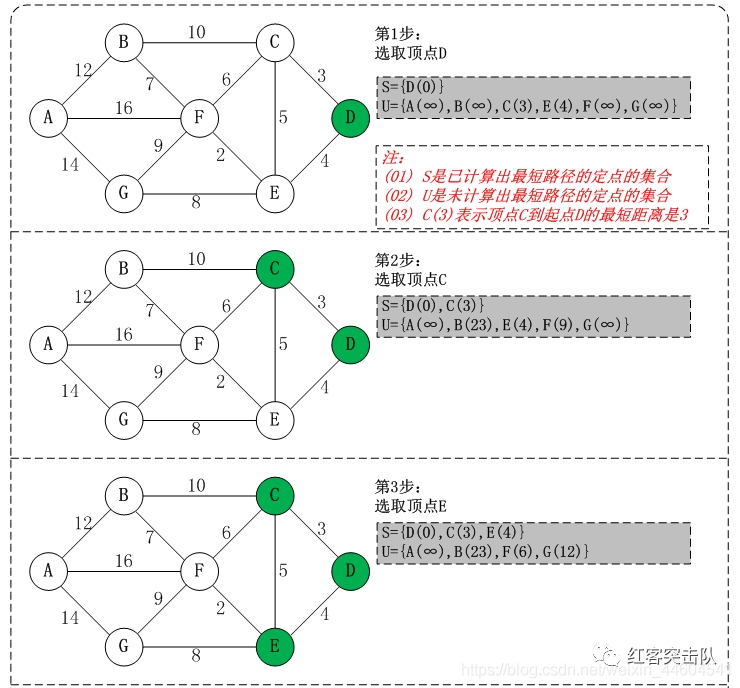
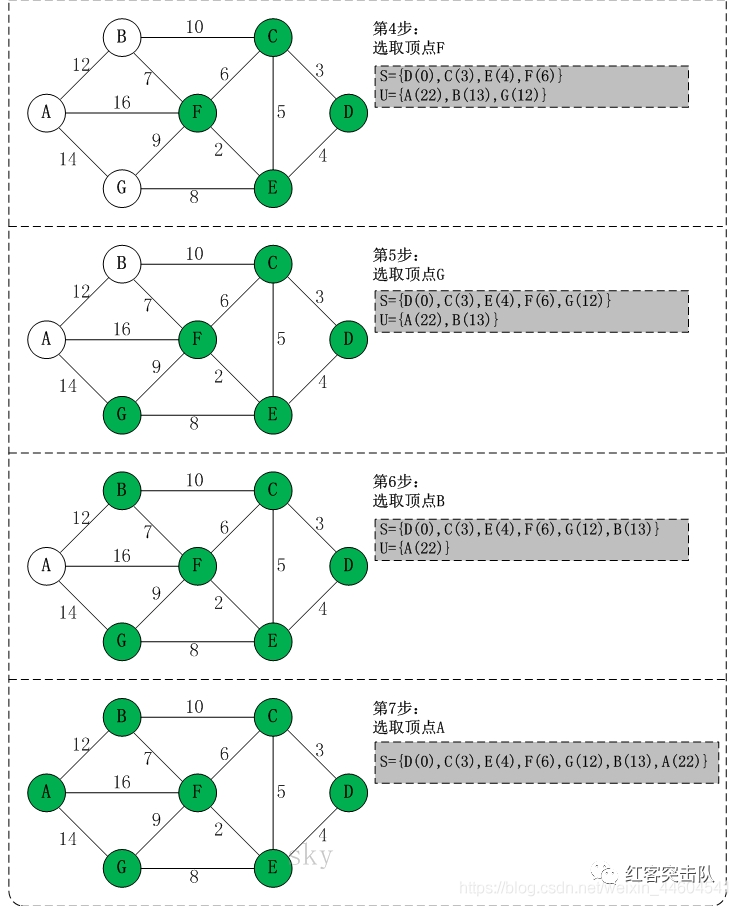
在本文最后有实例

2、Floyd-Warshall算法

Floyd算法是一个经典的动态规划算法
可以正确处理有向图或有向图或负权（但不可存在负权回路)
时间复杂度为O(N³)，空间复杂度为O(N²)

思路很简单

• 从任意节点i到任意节点j的最短路径不外乎2种可能：1、直接从i到j；2、从i经过若干个节点k到j

• 假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，检查Dis(i,k) + Dis(k,j) < Dis(i,j)
  是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，便设置Dis(i,j) = Dis(i,k) + Dis(k,j)
  

• 这样一来，当遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离

算法实现

• 引入两个矩阵：矩阵S中的元素a[i][j]
  表示顶点i(第i个顶点)到顶点j(第j个顶点)的距离；矩阵P中的元素b[i][j]
  表示顶点i到顶点j经过了b[i][j]
  记录的值所表示的顶点

• 初始时，矩阵D中顶点a[i][j]
  的距离为顶点i到顶点j的权值，如果i和j不相邻，则a[i][j]=∞
  ；矩阵P的值为顶点b[i][j]
  的j的值

• 第1次更新时，如果a[i][j]>a[i][0]+a[0][j]
  (a[i][0]+a[0][j]
  表示”i与j之间经过第1个顶点的距离”)，则更新a[i][j]
  为a[i][0]+a[0][j]
  ,更新b[i][j]=b[i][0]
  

• 同理，第k次更新时，如果a[i][j]>a[i][k-1]+a[k-1][j]
  ，则更新a[i][j]
  为a[i][k-1]+a[k-1][j]
  ,b[i][j]=b[i][k-1]
  

• 更新N次之后，操作完成

下面看个图例更好理解

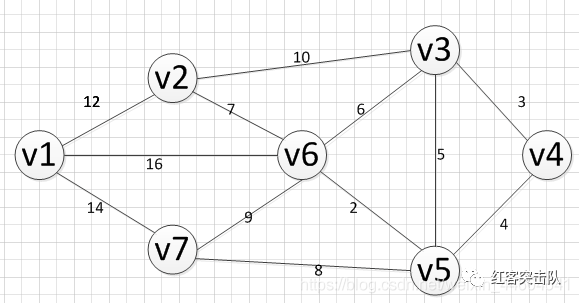
初始化矩阵

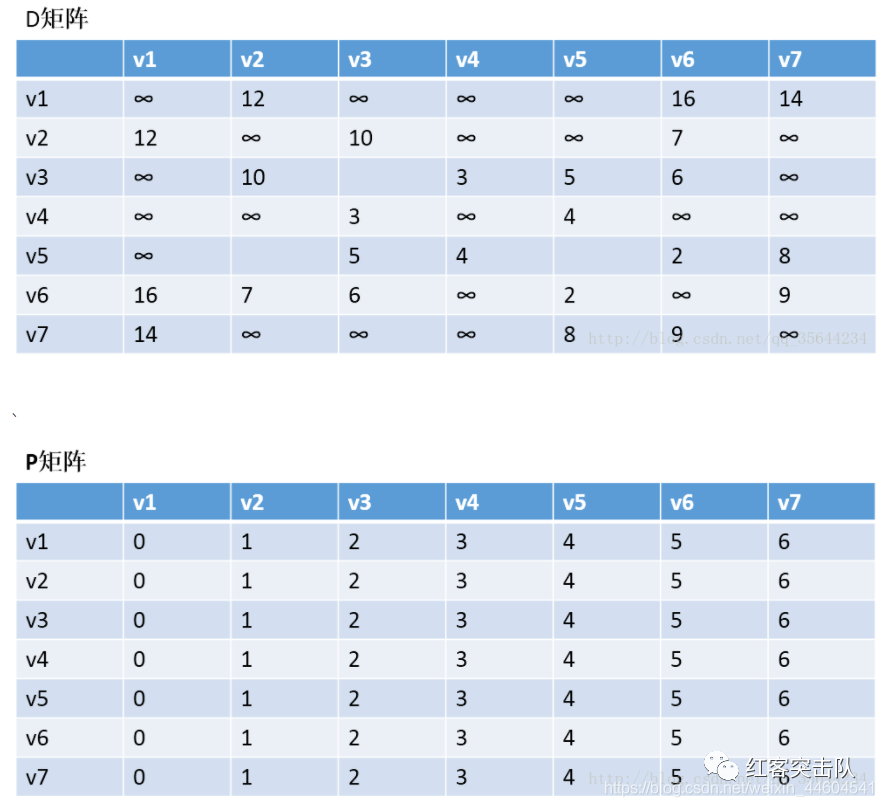
以v1为中阶，更新两个矩阵
发现，a[1][0]+a[0][6] < a[1][6]
和a[6][0]+a[0][1] < a[6][1]

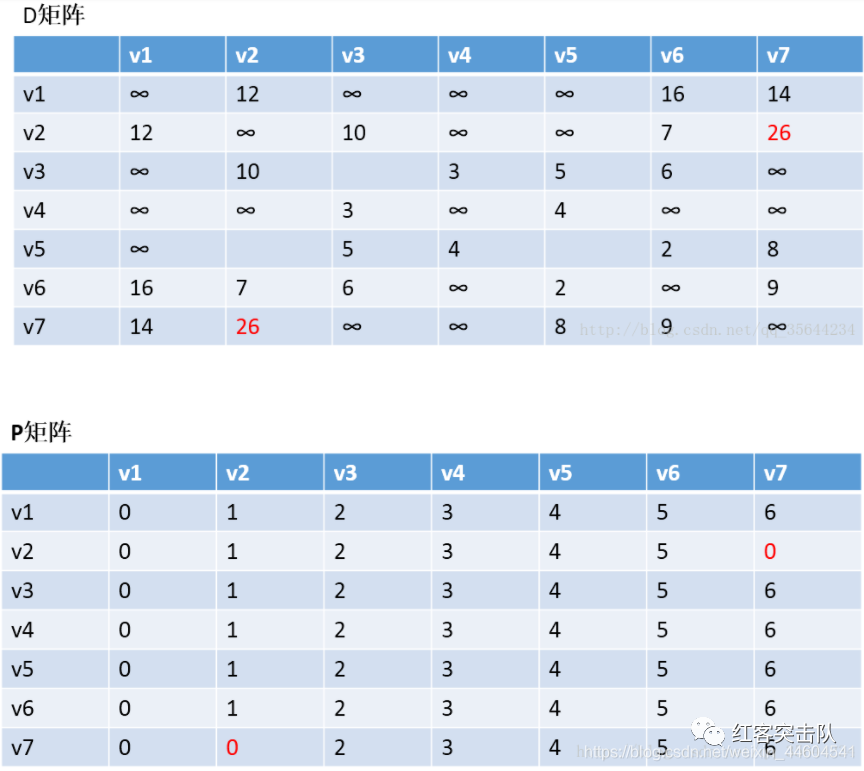
发现v2–v7的最短路径是：v2–v1–v7

以v2作为中介，来更新我们的两个矩阵

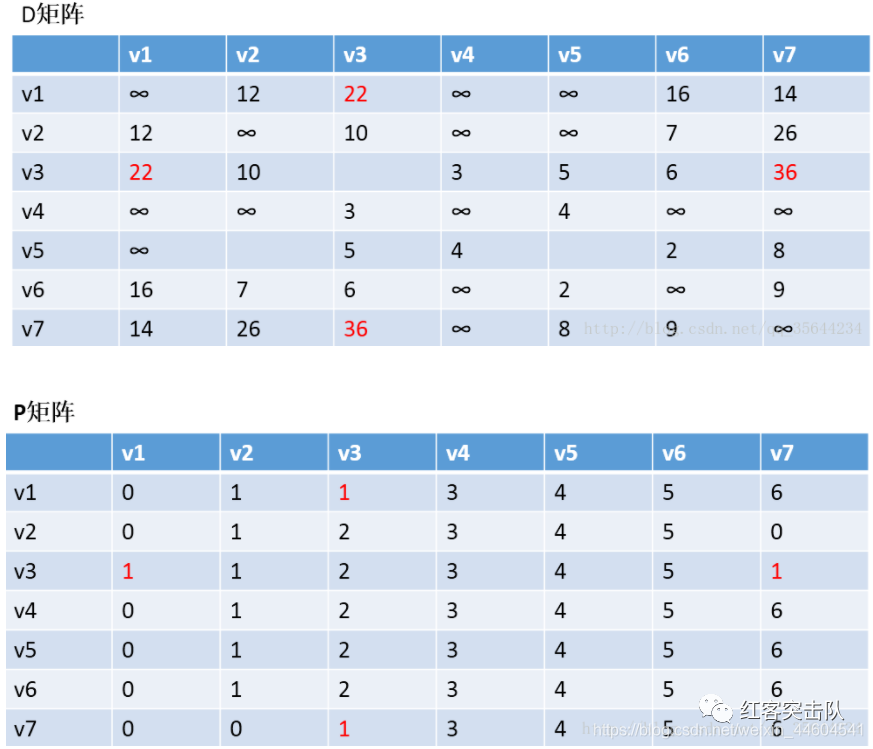
如此遍历全图，便能得到任意两点的最短路径

本文最后有实例

3、Bellman-Ford算法（SPFA算法）

可以处理负权图和判负环
稳定性较差
时间复杂度O(NE)， 空间复杂度O(N)

思路

• 用数组dis记录每个结点的最短路径估计值，用邻接表或邻接矩阵来存储图G

• 设立一个先进先出的队列用来保存待优化的结点，优化时每次取出队首结点u，并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作

• 如果v点的最短路径估计值有所调整，且v点不在当前的队列中，就将v点放入队尾

• 这样不断从队列中取出结点来进行松弛操作，直至队列空为止

• 如果某个点进入队列的次数超过N次则存在负环

下面看个图例更好理解

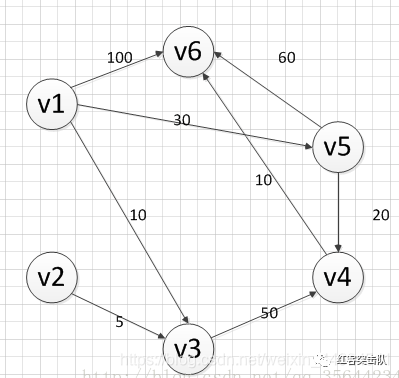
初始化数组dis

队列{v1}

第一次更新
v1出队列，然后，对以v1为弧尾的边对应的弧头顶点进行松弛操作

队列{v3，v5，v6}

第二次更新
v3出队列，然后，对以v3为弧尾的边对应的弧头顶点进行松弛操作

队列{v5,v6,v4}

。。。。。。

如此往复直到队列为空
得到v1到各个顶点的最短路径

本文最后有实例

4、实例：网络延迟时间

leet上743题

有 N 个网络节点，标记为 1 到 N。
给定一个列表 times，表示信号经过有向边的传递时间。
 times[i] = (u, v, w)，其中 u 是源节点，v 是目标节点， w 是一个信号从源节点传递到目标节点的时间。
现在，我们从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？
如果不能使所有节点收到信号，返回 -1。

Dijkstra算法
耗时740ms

class Solution:
    def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:
        dist = {i: float('inf') for i in range(1, N+1)}
        dist[K] = 0
        res = {}
        while dist:
            min_dis = min(dist.values())
            if min_dis == float('inf'):
                return -1
            for key, value in dist.items():
                if value == min_dis:
                    idx = key
            for time in times:
                if time[0] == idx and time[1] not in res.keys():
                    dist[time[1]] = min(dist[time[1]], dist[time[0]]+time[2])
            res[idx] = min_dis
            dist.pop(idx)
        return max(res.values())

Floyd-Warshall算法
耗时2080ms

class Solution:
    def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:
        d = [[float('inf')] * N for _ in range(N)]
        for time in times:
            d[time[0] - 1][time[1] - 1] = time[2]
        for i in range(N):
            d[i][i] = 0
        for k in range(N):
            for i in range(N):
                for j in range(N):
                    d[i][j] = min(d[i][j], d[i][k] + d[k][j])
        return -1 if float('inf') in d[K - 1] else max(d[K - 1])

Bellman-Ford算法（SPFA算法）
耗时1720ms

class Solution:
    def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:
        from collections import deque
        queue = deque()
        queue.append(K)
        dis = {i:float('inf') for i in range(1, N+1)}
        dis[K] = 0
        while queue:
            head = queue.popleft()
            for time in times:
                if time[0] == head:
                    distance = dis[time[0]] + time[2]
                    if distance < dis[time[1]]:
                        dis[time[1]] = distance

                        queue.append(time[1])
        return -1 if max(dis.values()) == float('inf') else max(dis.values())

结语

对最短路径的三种算法做了归纳

• 单源无负权用Dijkstra算法，消耗最小

• 单源有负权用Bellman-Ford算法（SPFA算法），消耗较大

• 任意两点有负权用Floyd-Warshall算法，消耗最大