本文会介绍搜索引擎的得分算法和模糊算法。
搜索,是每个人都会接触到的事情。搜索,依赖于搜索引擎。那么搜索引擎是怎么处理搜索的呢?本文通过两个算法的描述,让你理解其计算逻辑。
下面首先我们来介绍一下搜索引擎的权重得分算法——TF-IDF算法。
TF-IDF
比如短句“马伯庸的小说”,可以拆分为:马伯庸、的、小说 这三个关键字。在一个文档中要搜索“马伯庸的小说”,首先要对文档进行分析,因为一个文档出现的词很多,那么在分析的时候,就需要对这三个词出现的频次分别进行记录。记录完频次,然后需要计算这些词在文档中占的权重,这个就是词频(Term Frequency)
。
假设该文档有100个词,马伯庸出现了3次,的出现了30次,小说出现了5次。那么他们的词频就是0.03、0.30、0.05。而短句“马伯庸的小说”在这个文档中的词频就是0.38。
因此,一个简单的度量文档和搜索词汇的相关性的方法,就是将各个关键词在文档中出现的总词频。
他的公式是
补充知识:在搜索引擎中有一类特殊词是毫无意义的,是需要排除掉的。比如英语中的and、or、this、is、to、be等,汉语中的 是、的、吗、嘛等,对这类词的分析是没有意义的(此处不考虑文言文等特殊情况,特殊情况可以添加分词,后话再说)。这类词称之为`停止词(stopword)`。对于这一部分词,一般情况下我们是不需要计算权重的。针对于短句“马伯庸的小说”分成的三个关键字,“的”已经被忽略。剩下“马伯庸”和“小说”。而“马伯庸”是特指,“小说”就比较泛,所以前者的相关性肯定比后者重要。因此我们有时也会在查询时适当的添加权重。
下面说一下IDF(Inverse Document Frequency,逆文本频率)
。
假设有如下文档:
| id | 内容 |
|---|---|
| 1 | 牛顿在树下记笔记时,被苹果砸到了。 |
| 2 | 牛顿放下笔记本,望向那个苹果。这一切被路人记录在笔记本里。 |
| 3 | 乔布斯看到牛顿被砸了,发明了苹果笔记本来纪念这件事。 |
当我们在上面的文档中搜索“苹果笔记本”时,会分词为“苹果”、“笔记”、“笔记本”、“苹果笔记本”,如果按照上面的TF算法,因为文档2多次出现“笔记本”、“苹果”等词汇,文档2的词频是最高的。但是我们更希望文档3作为第一条记录。这也就是IDF产生的原因。
这个时候就需要IDF权重算法了。概括的讲,当一个关键词在
应用到上面的数据中:
苹果出现了3次,单次权重为
笔记出现了4次,单次权重为
很直观的可以看到,文档3在“苹果笔记本”中具有更高的得分。
要计算每个文档的最终权重,需要结合TF和IDF算法结合,他们的公式是: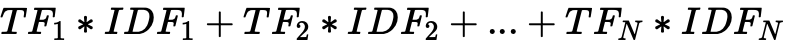
所以对于搜索词“苹果笔记本”,在每个文档中的权重为:
文档1:苹果(*1)+笔记(
文档2:苹果(*1)+笔记(
有人会纳闷为什么还会有负数?这是因为样本基数不够大而导致的。当文档足够多时,就不会出现词频比文档还多的情况,就不会出现负数了。
至此,我们已经算出了上面文档对于搜索词“苹果笔记本”的权重。
通过TF-IDF,我们可以很清晰的知道这个词的权重对于当前查询来说,提供了多少信息。
Fuzzy
我们从下面几个日常情景中体会下搜索引擎与模糊查询:
情景一
我们在百度搜索“法外狂徒”,就会提示出“张三”等等一共最多10条。我们从中选择一条。这种情况是常见的,我们一般只需要记住开头的文字就可以了。
从上面的TF-IDF算法中,我们得知了搜索引擎系统会给每个词进行分词。当搜索引擎命中要搜索的词时,对于每一个词,会从底层的数据结构FST中向后拓展若干字符,取出所有的短句。这种联想的方式叫做Completion Suggest
。
情景二
当有时候,我们输入了张三,也会弹出法外狂徒,此时是搜索引擎对张三和法外狂徒进行了同义词联结。同义词(synonym)
,当搜索其中一个词时,另外一个词也会在搜索之列。
情景三
当我们在百度搜索“法外小徒”,同样也会提示出“张三”等等一共最多10条。我们从中选择一条。
当我们搜索错误的词时,搜索引擎没有搜索到对应的词。此时他会尝试修改一两个字符来进行搜索。
比如“法外小徒”和“法外狂徒”,将“小”修改为“狂”,修改一个字就可以达到预期的效果。这种修改一个字的操作,叫一个编辑距离(Levenshtein Distance)
。同样的操作,还有交换、删除、新增等。
情景四
当我们在百度搜索“法在小徒”,这时什么提示都没有,甚至搜索的话,都不是我们想看到的内容。
正如上面而言,是可以执行N个编辑距离操作来达到查询正确的目的。
但是这个编辑距离并不是可以无限大的,一般有限制最多执行2次。因为当步长太大时,1)会影响查询的效率,这个步长操作是计算所有相关短句的相关性。而如果步长太大,导致计算的短句数量暴增,会导致查询阻塞。
一般情况下,0~1个字符是不会纠错的,1~5个字符最多执行1个编辑距离,5~9个字符最多是两个编辑距离。
对于长度为4的英文单词,如果只有1个编辑距离,那么他可以比较的最大单词量为
编辑距离的计算
那么编辑距离一般是怎么计算的呢?
首先将要对比的两个词分别写在正上和正左,并写好对应的标号。
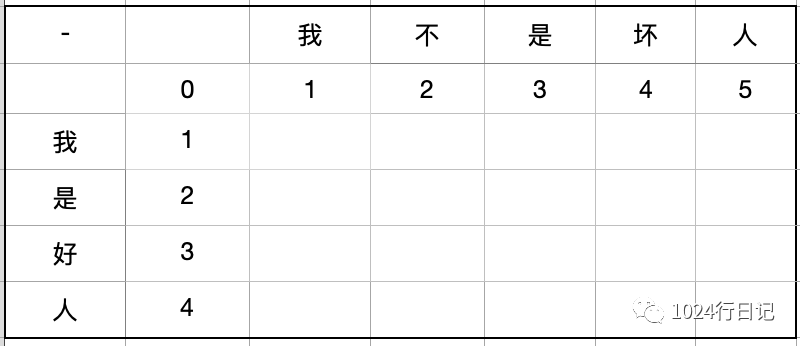
然后进行比对。在正左的第一个字和正上的第一个字的单元格中,进行比较以它为右下角的四格单元格中,最小的数字。
获得这个数字后,如果这两个字相等,那么直接填入右下角的单元格,否则该数字+1后填入该单元格。
结果如下图所示,蓝色的横向和纵向是相等的,填入最小的数字0。红色的横向和纵向是不相等的,填入最小的数字+1后的值。
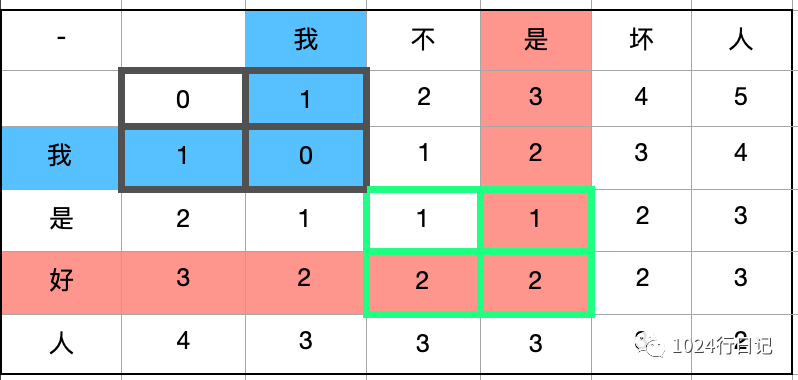
矩阵演示只演示了增删改,并不能演示交换的效果
java代码演示:
public static void main(String[] args) {
String x = "我是好人";
String y = "我不是好人";
int xl = x.length();
int yl = y.length();
int[][] dis = new int[xl + 1][yl + 1];
// 初始化二位数组
for (int i = 0; i <= xl; i++) {
dis[i][0] = i;
}
for (int j = 0; j <= yl; j++) {
dis[0][j] = j;
}
int eq = 0;
for (int i = 1; i <= xl; i++) {
for (int j = 1; j <= yl; j++) {
if (x.charAt(i - 1) == y.charAt(j - 1)) {
eq = 0;
// 交换的处理
} else if (i < x.length() && j < y.length() &&
x.charAt(i - 1) == y.charAt(j) && x.charAt(i) == y.charAt(j - 1)) {
eq = 0;
} else {
eq = 1;
}
dis[i][j] = Math.min(
Math.min(dis[i - 1][j] + 1, dis[i][j - 1] + 1), dis[i - 1][j - 1] + eq);
}
}
System.out.println("x:{" + x + "}和y:{" + y + "}的编辑距离为:" + dis[xl][yl]);
}






