最近实现一个小功能,IP 路由,就是基于 IP 进行定位。学习使用了 HashTree 这种结构,HashTree 可以快速的进行大量整数的检索,在 IPv4或IPv6 作为关键字检索时,很有用。本文介绍一下 HashTree。
哈希树 Hash Tree
哈希树,基于质数分辨定理构建的利用余数分辨大量整数的树形结构。例如深度为10的哈希树可以分辨 6464693230(2x3x5x7x11x13x17x19x23x29= 6464693230) 个整数,而深度为100的哈希树可以分辨 4.711930e219 个整数。而深度为 H 的树只需要完成 H 次取余运算即可完成分辨,意味着10次取余运算,即可完成分辨 6464693230 个数,而100次取余运算即可完成分辨4.711930e219个数,效率很高,分辨性很强。可以用于 IP 路由等可以用整数作为关键字进行检索的场景。具有结构简单、检索迅速、删除节点结构不变等优点。缺点是不能基于关键字排序。
之所以可以使用余数的H次运算即可分辨大量的整数,是基于质数分辨定理来实现的。质数分辨定理简单的说就是 N 个质数可以精确分辨 N 个质数乘积个整数,也就是说这些 N 个质数乘积个整数对 N 个质数求余,不可能存在完全相同的余数序列。
例如:2 个连续质数:2,3,就可以分辨 2x3 = 6 个整数 1,2,3,4,5,6。我们用这些整数对 2, 3 分别求余:
| mod | 2 | 3 | 余数序列 |
|---|---|---|---|
| 1 | 1 | 1 | 1,1 |
| 2 | 0 | 2 | 0,2 |
| 3 | 1 | 0 | 1,0 |
| 4 | 0 | 1 | 0,1 |
| 5 | 1 | 2 | 1,2 |
| 6 | 0 | 0 | 0,0 |
可见,使用连续质数2,3,就可以通过余数序列分辨 6 个数。这6个数的余数序列不会相同的。
关于质数分辨定理的证明请移步:质数分辨定理的数学证明章节。
基于此的哈希树结构具有如下特征:
子节点的数量与连续的质数相同。假如是十层的话,根节点为2个子节点,而第二、三、四、五、六、七、八、九层为为3、5、7、11、13、17、19、23、19个子节点
节点的边用余数表示,对质数求余来确定边
节点的 key,就可以记录该数及其他信息
若分辨数时,当前余数节点已经存在其他数,则继续对下层质数求余
如图所示:
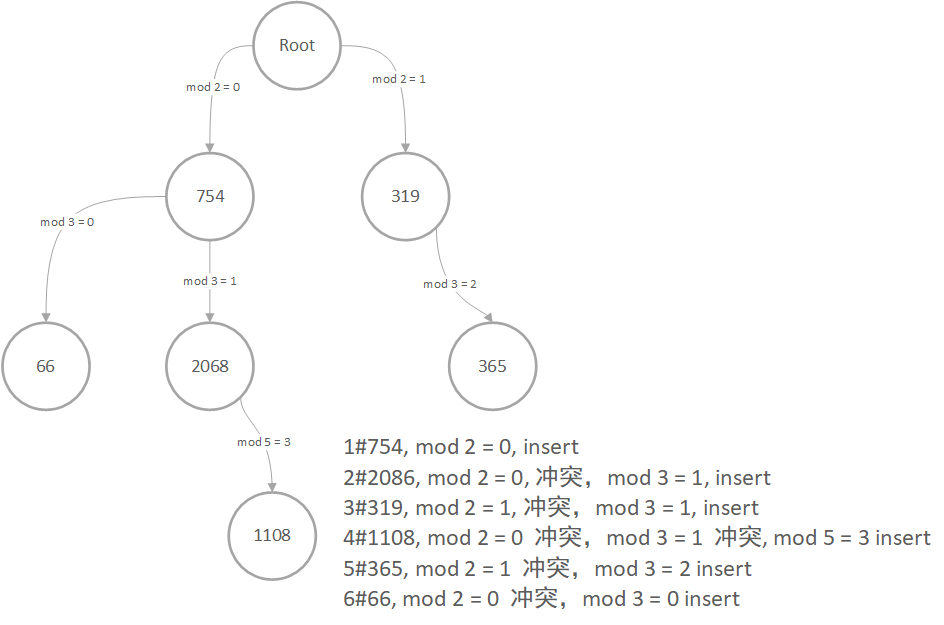
此图展示了,754, 2068, 319, 1108, 365, 66 这几个数,插入到哈希树中的结果。
其中,节点的边,表示对某个质数求余,质数基于数层级,依次为 2, 3, 5, 7, 11… 这些连续的质数个。节点拥有的最大子节点数为当层的质数。
哈希树支持插入,查找,删除等操作。
结构操作说明
哈希树节点结构
每个节点需要存储 key 用于标识,也就是所分辨的数。
value 表示 key 对应的数据,例如 ip 路由中,key 就是 ip,而value 就是该 ip 的路由信息。
需要记录全部子节点,通过余数标识。
具体实现请看代码。
插入操作
依次利用质数取余,若计算得到对应的节点不存在,则插入该节点位置即可。若节点存在,以下个质数取余,直到插入。
参考代码。
搜索操作
过程类似,检索余数对应节点的 key 是否为检索到 key,不是,继续向下级节点检索,直到找到 key 或者节点遍历结束。
参考代码。
删除操作
搜索节点过程类似,当确定节点后,将节点的 key 设为特定数据(本例中为 -1)表示已删除(未占用),将 value 数据清空。不需要处理子节点。
参考代码。
编码
定义 HashTree
和 hashTreeNode
:
1type HashTree struct {
2 Root *HashTreeNode // 根节点
3 Height int // 高度
4 Primes []int // Height 个连续的质数集合
5}
6
7func NewHashTree() *HashTree {
8 return &HashTree{
9 Root: NewHashTreeNode(-1), // 根节点 key
10 Height: 10,
11 Primes: []int{2, 3, 5, 7, 11, 13, 17, 19, 23, 29},
12 }
13}
14
15type HashTreeNode struct {
16 Key int // 节点 Key, key == -1 表示节点未被占用
17 Value interface{} // 依托与 key 的数据
18 childNodes map[int]*HashTreeNode // 子节点
19}
20
21func NewHashTreeNode(key int) *HashTreeNode {
22 return &HashTreeNode{
23 Key: key,
24 Value: nil,
25 childNodes: map[int]*HashTreeNode{},
26 }
27}
插入 key:
1// 插入
2func (ht *HashTree) Insert(key int, value interface{}) *HashTree {
3 node := ht.Root
4 pi := 0
5 for {
6 m := key % ht.Primes[pi]
7 if childNode, exists := node.childNodes[m]; exists && childNode.Key != -1 {
8 // 节点存在,且被占用
9 node = childNode
10 pi++
11 continue
12 }
13 node.childNodes[m] = &HashTreeNode{
14 Key: key,
15 Value: value,
16 childNodes: map[int]*HashTreeNode{},
17 }
18 break
19 }
20 return ht
21}
查找 key
1// 查找
2func (ht *HashTree) Search(key int) *HashTreeNode {
3 node := ht.Root
4 pi := 0
5 for {
6 m := key % ht.Primes[pi]
7 if childNode, exists := node.childNodes[m]; !exists {
8 return nil
9 } else if childNode.Key == key {
10 return childNode
11 } else {
12 node = childNode
13 pi++
14 continue
15 }
16 }
17}
删除 key
1// 删除
2func (ht *HashTree) Delete(key int) *HashTree {
3 node := ht.Root
4 pi := 0
5 for {
6 m := key % ht.Primes[pi]
7 if childNode, exists := node.childNodes[m]; !exists {
8 // key 不存在,空操作
9 break
10 } else if childNode.Key == key {
11 // 找到,删除。将 key 设为 -1 表示未占用
12 childNode.Key = -1
13 childNode.Value = nil
14 break
15 } else {
16 node = childNode
17 pi++
18 continue
19 }
20 }
21 return ht
22}
测试
1func main() {
2 ht := NewHashTree()
3 ht.Insert(10, "some 10 Value")
4 ht.Insert(20, "some 20 Value")
5 fmt.Println(ht.Search(20)) // &{20 some 20 Value map[]}
6 fmt.Println(ht.Search(10)) // &{10 some 10 Value map[2:0xc0000044c0]}
7 fmt.Println(ht.Search(30)) // <nil>
8 ht.Delete(10)
9 fmt.Println(ht.Search(10)) // <nil>
10 fmt.Println(ht.Search(20)) // &{20 some 20 Value map[]}
11}
质数分辨定理的数学证明
来自网络的图片:

难道质数真的是宇宙的奥秘?






