前言
本文为首先将马尔可夫链进行推广，介绍了马尔可夫决策过程、强化学习理论并阐明了两者间的联系。其次对比分析了强化学习中常用的两种算法：Q-learning 和 Sarsa。文章最后部分展示了在Python 搭建的强化学习环境下人工智能小方块是如何在环境中进行训练、完成简单的走出迷宫的学习任务。（请耐心读下去哦~后文还是很有趣的）
1. 马尔可夫决策过程
近年来，随着数据存储能力的大幅提高、计算机算力的突飞猛进，人工智能、机器学习等领域得到了越来越多的关注，许多统计学家也开始进行机器学习相关研究。强化学习作为一种以环境反馈为输入的适应环境的机器学习方法，在实际中得到了广泛的应用。
1907年，俄国数学家安德雷·马尔可夫提出马尔可夫链的概念，将具有马尔可夫性质且存在于离散的指数集和状态空间的随机过程称为马尔可夫链。概率论中，马尔可夫性质指在状态转移过程中从一个状态转移到另一个状态，下一个状态的产生只与当前的状态有关而与之前的状态无关，即“无后效性”。记所研究的随机过程为,状态空间记为，表示状态，则马尔可夫性可表示为：
对具体的状态 ,将它们之间的状态转移概率 (由状态 i 转移到状态 j) 定义为： 。假如状态空间中有n种状态可供选择，定义状态转移矩阵为：
由概率的相关性质，可以看出具有性质：
(1) ;
(2)
马尔可夫过程包括状态空间和个状态之间转移的概率,是一个二元组，主要描述的是状态之间的转移关系。若在各状态的转移关系上赋予不同的奖励值以及决策过程的阻尼系数，即可由此得到马尔可夫奖励过程。强化学习中，智能体和环境通过执行动作进行交互，状态的转移由于动作的执行而产生，因此，在马尔可夫奖励过程的基础上添加动作空间，我们可定义相应的马尔可夫决策过程.
定义：马尔可夫决策过程
马尔可夫决策过程(Markov Decision Process, MDP)由 五元组组成，其中：
表示状态空间,有 ， 为第i步的状态。
表示动作空间，有 ， 为第i步的动作。
为在某一状态 下，采取动作 ，转移到新一状态 的概率。
表示决策过程的一个阻尼系数。
为奖励函数，表示在当前状态下采取动作到达下一状态时环境对智能体的反馈。
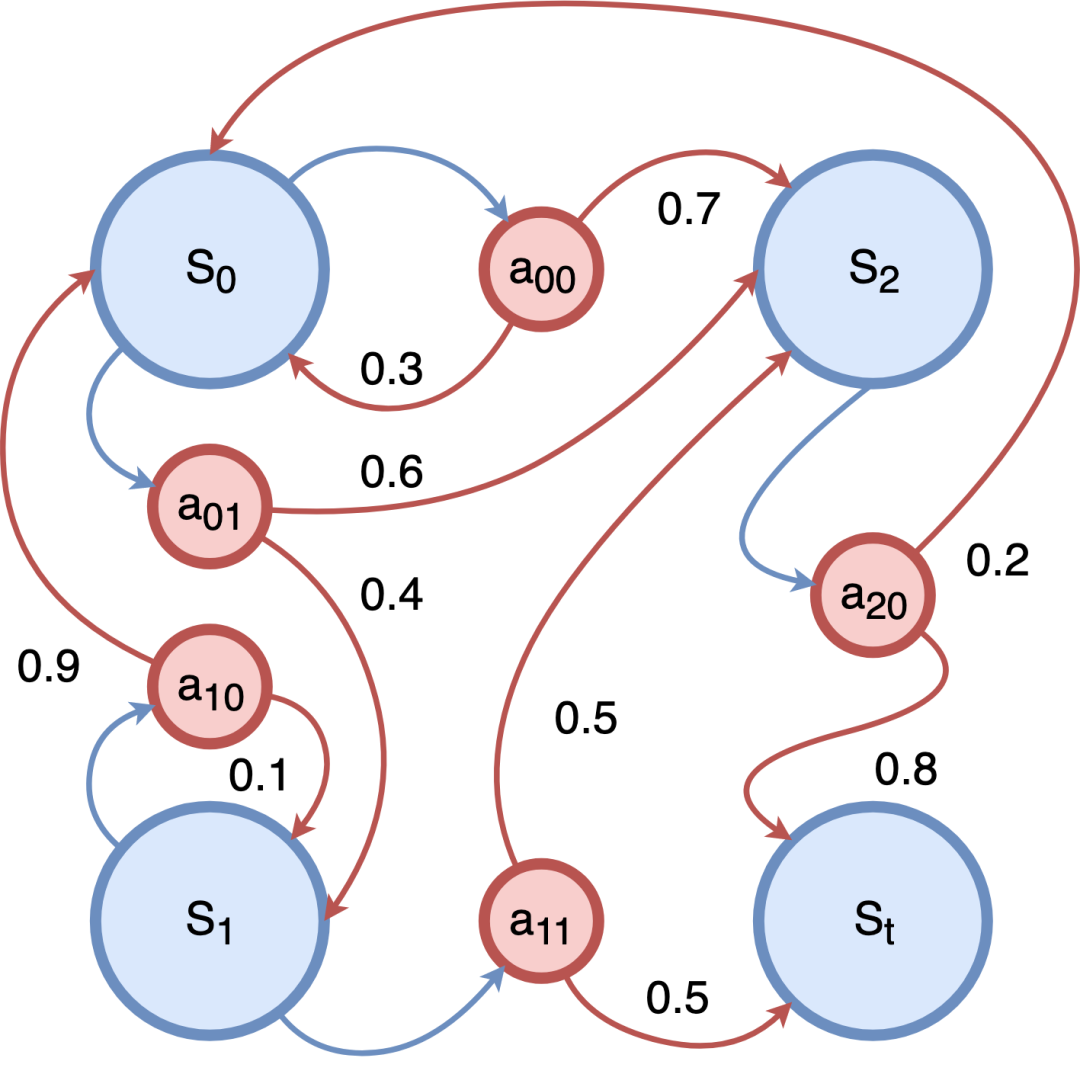
强化学习中，MDP 基于智能体和环境进行构建。在 MDP 模拟时，智能体会感知当前的系统状态，按策略对环境实施动作，从而改变环境的状态并得到奖励，奖励随时间的积累被称为回报。
MDP 的历史可以追溯至20世纪50年代动力系统研究中的最优控制问题，1957年，美国学者 Richard Bellman 通过离散随机最优控制模型首次提出了离散时间马尔可夫决策过程。1960 年和 1962 年，美国学者 Ronald A. Howard 和 David Blackwell提出并完善了求解MDP模型的动态规划方法。进入 1980s 后，学界对 MDP 的认识逐渐由“系统优化”转为“学习”。1987年，美国学者 Paul Werbos 在研究中试图将 MDP 和动态规划与大脑的认识机制相联系。1989 年，英国学者 Chris Watkins 首次在强化学习中尝试使用 MDP 建模。Watkins (1989) 在发表后得到了机器学习领域的关注，MDP 也由此作为强化学习问题的常见模型而得到应用。
2. 强化学习
强化学习 (Reinforcement learning, RL) 是机器学习领域内的研究热点，主要用来实现决策优化，在智能游戏、机器人控制、计算机视觉、自然语言处理和推荐系统等领域应用广泛。不同于监督学习和非监督学习，强化学习不要求预先给定任何数据，而是通过接收环境对动作的奖励（反馈）获得学习信息并更新模型参数，其基本要素有策略(Policy)、奖赏函数(Reward Function) 、值函数(Value Function)、环境模型(Environment)，通常使用马尔可夫决策过程来描述。其近30年发展历程大致如下：
1992年Watkins 提出Q-learning 算法。 1994年Rummery 提出Saras算法。 1996年Bersekas提出解决随机过程中优化控制的神经动态规划方法。 2006年Kocsis提出了置信上限树算法。 2009年Kewis提出反馈控制只适应动态规划算法。 2014年Silver提出确定性策略梯度（Policy Gradients）算法。 2015年Google-deepmind 提出Deep-Q-Network算法。 2016年-Now 大量深度强化学习算法涌出。
强化学习把学习看作试探评价过程，智能体选择一个动作用于环境，环境接受该动作后状态发生变化，同时产生一个强化信号 (奖或惩) 反馈给智能体，此时智能体根据强化信号和环境当前状态再选择下一个动作。因此，强化学习的目标是学习一个行为策略，使得智能体能够获得环境最大的奖赏。
2016年3月， 基于深度强化学习的机器人 Alpha Go 与围棋世界冠军、职业九段棋手李世石进行围棋人机大战，获得大胜。随着 Alpha Go 登上 Nature，强化学习受到了越来越多的关注 ，已成为当下机器学习中最热门的研究领域之一。
3. 贝尔曼方程
Bellman 方程是强化学习的基础和核心，下文将提到的 Q-learning和 Sarsa 也是通过 Bellman 方程求解马尔科夫决策过程的最佳决策序列。下面我们介绍贝尔曼方程的三个主要概念，策略函数、状态价值函数、状态-动作价值函数。
策略函数（Policy Function）：策略函数是一个输入为s输出为a的函数表示为 ，其中s表示状态，策略函数的含义就是在状态s下应该选择的动作。
状态价值函数（State Value Function）：强化学习的核心问题是最优化策略函数，那么如何评价策略函数是最优的呢？状态价值函数是评价策略函数 优劣的标准之一，在每个状态s下，可以有多个动作a选择，每执行一次动作，系统就会转移到另一个状态，如何保证所有的动作能使系统全局最优则要定义价值函数，系统的状态价值函数的含义是从当前状态开始到最终状态时系统所获得的累加回报的期望，下一状态的选取依据策略函数（不同的动作a将导致系统转移到不同的状态）。所以系统的状态价值函数和两个因素有关，一个是当前的状态s，另一个是策略 。从不同的状态出发，得到的值可能不一样，从同一状态出发使用不同的策略，最后的值也可能不一样。所以建立的状态价值函数一定是建立在不同的策略和起始状态条件下的。状态价值函数的具体形式如下：
其中 ，其中 表示从 转移到 时获得的回报， 是折损因子。可以将上面的状态价值函数的形式表示为递归的形式：
最优累计期望可用 表示, 可知最优值函数就是 。
状态动作价值函数（State-action Value Function）：动作价值函数也称为Q函数，相比于Value Function是对状态的评估，Q Function是对（状态-动作对）的评估，Q值的定义是，给定一个状态 ，采取动作 后，按照某一策略 与环境继续进行交互，得到的累计汇报的期望值。其数学表达形式是：
最优价值动作函数
对于状态价值函数和动作价值函数的区别，可以简单的认为，状态函数中，当前状态下选取哪个动作是未知数，需要求出一系列的动作集合（各不同状态下），形成一个完整的策略，然后使状态方程的值最大化，而动作价值函数是当前状态下的动作已知，求余下状态下的动作集合使动作方程的值最大化。
Bellman方程实际上就是价值动作函数的转换关系：
将公式（4）代入公式（3）可得：
4. 时序差分学习方法
时序差分方法(Temporal difference, TD)，是强化学习中求解马尔可夫决策环境最为广泛的一种学习方法。它结合了蒙特卡罗方法与动态规划方法，首先它可以像蒙特卡罗方法那样直接从经验中进行学习而不需要知道完整的环境模型，同时它又可以像动态规划方法那样根据已学习到的价值函数的估计进行当前估计的更新(步步更新)，而不需等待整个episode结束。值函数计算方式如下:
下面将介绍时序差分方法中的两种经典算法：Q-learning 和 Sarsa。
4.1 Q-learning
Q-learning 实际是一个决策过程，其目的是学习特定状态下、特定动作的价值，使用时序差分学习方法进行离线学习，用 Bellman 方程对马尔科夫过程求解最优策略。Q-learning 算法学习前首先建立一个 Q-Table，Q-Table 以状态为行、动作为列，通过不断采取动作带来的奖赏对 Q-Table 进行更新，Q-learning 算法如下所示：
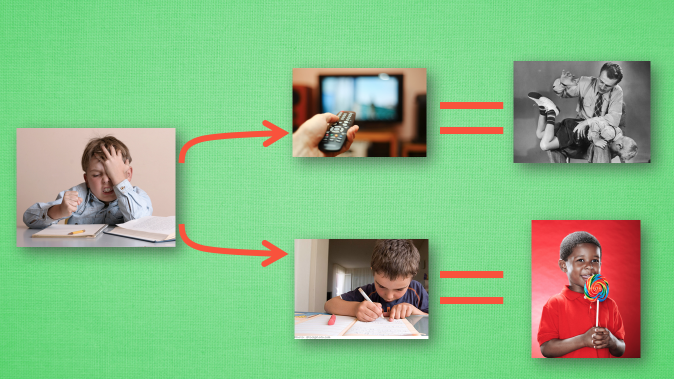
举一个简单的例子解释 Q-learning 算法，假设现在小明处于写作业的状态 s1 且小明以前没尝试放弃写作业去看电视, 他的动作空间包含：1.继续写作业 2.跑去看电视。因为以前没有被罚过，所以小明选看电视，然后现在的状态变成了看电视，接着小明继续选看电视，后来爸妈回家，发现小明没写完作业就去看电视了，狠狠地惩罚了他一次，他深刻地记下了这一次经历，并将 “没写完作业就看电视”这种行为更改为负面行为。
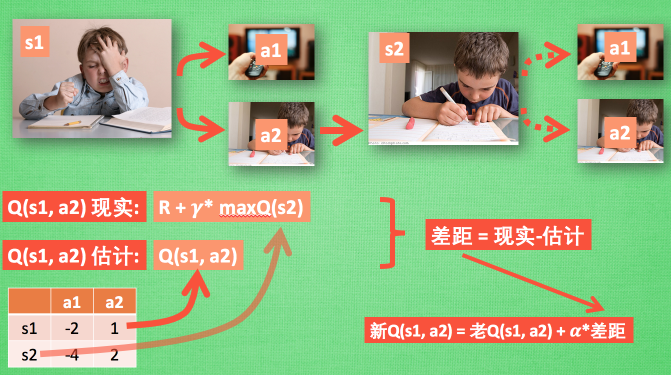
在上一轮学习过后, 现在小明再次处于写作业的状态 s1，其仍有两个可选动作：看电视 a1、写作业 a2，根据上次的经历，在这种 s1 状态下，写作业 a2 带来的潜在奖励要比 a1 看电视高，这里的潜在奖励可以用一个有关于 s 和 a 的 Q 表格代替,如。在 Q-table 中, Q(s1, a1)=-2 要小于 Q(s1, a2)=1, 所以小明的决策为 a2。对应的状态更新成 s2，此时小明还是有两个同样的选择, 重复上面的过程，在行为准则Q 表中寻找 Q(s2, a1) Q(s2, a2) 的值, 选取较大的一个。然后继续重复上面的决策过程。
根据 Q 表的估计，因为在 s1 中，a2 的值比较大， 通过之前的决策方法，小明在 s1 采取了 a2, 并到达 s2，这时更新用于决策的 Q 表， 接着他并没有在实际中采取任何行为, 而是再想象自己在 s2 上采取了每种行为, 分别看看两种行为哪一个的 Q 值大, 比如说 Q(s2, a2) 的值比 Q(s2, a1) 的大, 所以将大的 Q(s2, a2) 乘上一个衰减值 并加上到达s2时所获取的奖励 R (这里还没有获取到奖励, 所以奖励为 0), 因为会获取实实在在的奖励 R , 所以将这个作为现实中 Q(s1, a2) 的值, 但是之前是根据 Q 表估计 Q(s1, a2) 的值有了现实和估计值, 就能更新Q(s1, a2) , 根据估计与现实的差距，将这个差距乘以一个学习效率 累加上老的 Q(s1, a2) 的值变成新的值.
Q-Learning 是一种异策略离线学习算法，其行动策略是ε-greedy策略，Q-table的更新策略是贪婪策略。异策略是指行动策略和评估策略不是一个策略。
4.2 Sarsa
Sarsa 算法全称是state-action-reward-state-action。其也是采用 Q-table 的方式存储动作值函数，而且决策部分和 Q-Learning 一样采用ε-greedy 策略。Sarsa 算法如下所示：
4.3 两种算法的差别
Sarsa是on-policy的更新方式，其行动策略和评估策略都是ε-greedy策略。Q-Learning 是 off-policy 的，其行动策略是ε-greedy 策略，Q-table 的更新策略是贪婪策略。
Q-Learning 算法是先假设下一步选取最大奖赏的动作，更新值函数。然后再通过 ε-greedy 策略选择动作。而 Sarsa 算法是先通过 ε-greedy 策略执行动作，然后根据所执行的动作，更新值函数。
5. 强化学习实际应用
本部分笔者使用 Python 模拟搭建了一个智能迷宫环境。此次学习的目的是使智能体在迷宫中通过不断的探索及试错，最终能够避开陷阱找到通往宝藏的最佳路径。
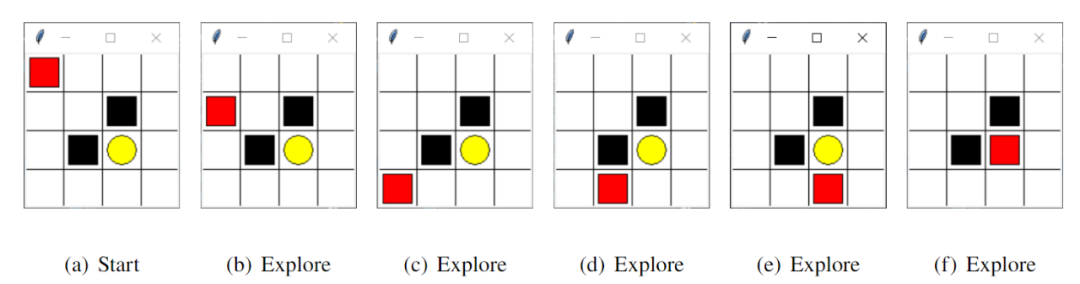
如图10所示，本次学习状态空间共有 个元素，记为，图中红色小方块代表智能体，可选动作为上、下、左、右（0，1，2，3），白色方块表示普通路径，对应奖励值记为 0，黑色方块代表陷阱，对应奖励值设置为 -1，黄色圆圈表示宝藏，对应奖励值设置为 +1。若智能体落入陷阱或者找到宝藏则此轮学习结束，进入下一轮新的学习。本文将最大探索次数设置为 13 次，也即是说如果在 13 步之内智能体没有找到宝藏则进入新的一轮学习。奖励衰减系数设置为 0.9，随着探索次数的增加得到的奖励值会衰减，以此促使智能体快速找到宝藏。学习率设置为 0.1，控制 Q-table 的更新速度。贪婪系数设置为 0.9，也即是说智能体有 90% 的机率选择Q-table中值最大的动作，10% 的机率随机等概率选取动作。
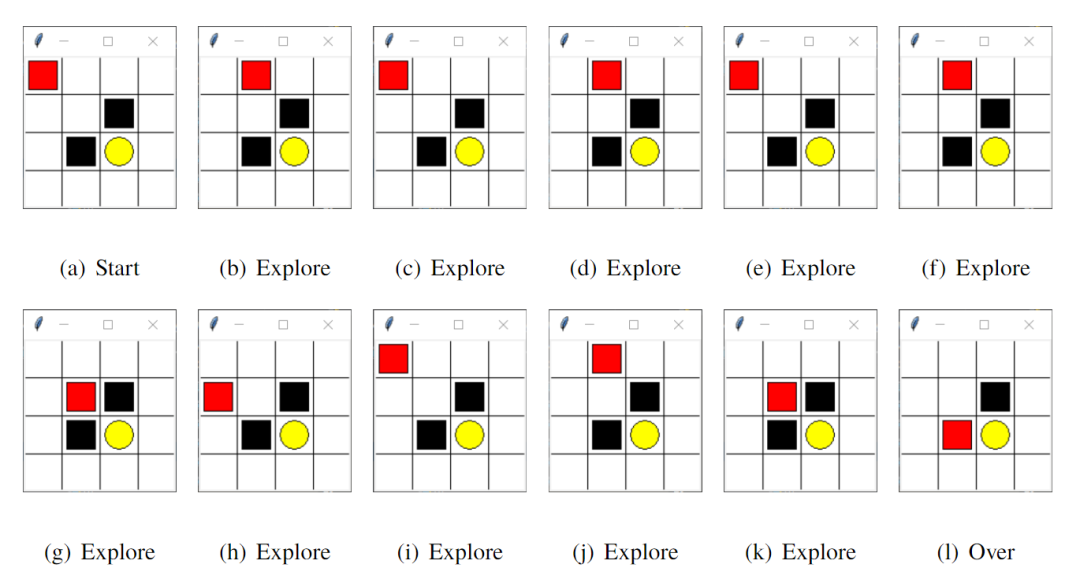
因环境较为简单，Q-learning 算法与 Sarsa 算法在本环境中运行效果差异不大。以 Q-learning 算法为例进行介绍，其核心Q-table的行和列分别表示状态和动作，Q-table的值 Q(s,a) 衡量了当前状态采取的动作的优质程度。游戏开始时智能体的初始位置为 ，其可选动作为向右或向下移动。由于智能体对环境一无所知，所以我们首先将 Q-table 中的值初始化为零，Q-table 中各个值相等，所以智能体会等概率随机选取动作，如图12所示，智能体首先向右移动从 状态到达了 状态，并将状态 及在该状态下的三个可选动作下、左、右添加近 Q-table，状态 奖励值为 0，按照公式 更新Q-table 后得到下图 ，后续步骤与上述类似。第一轮学习经过 11 步之后智能体落入陷阱，进入下一轮探索。
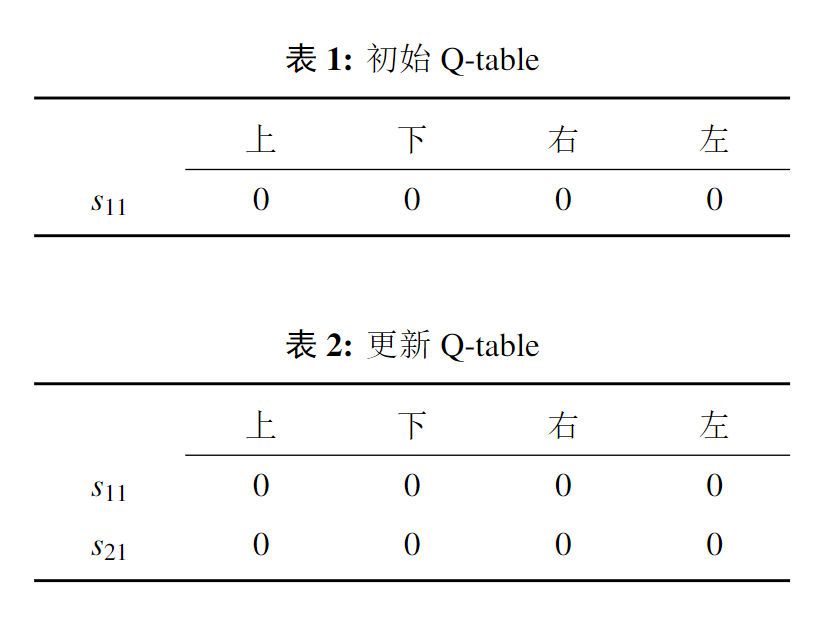Fig11. Q-table
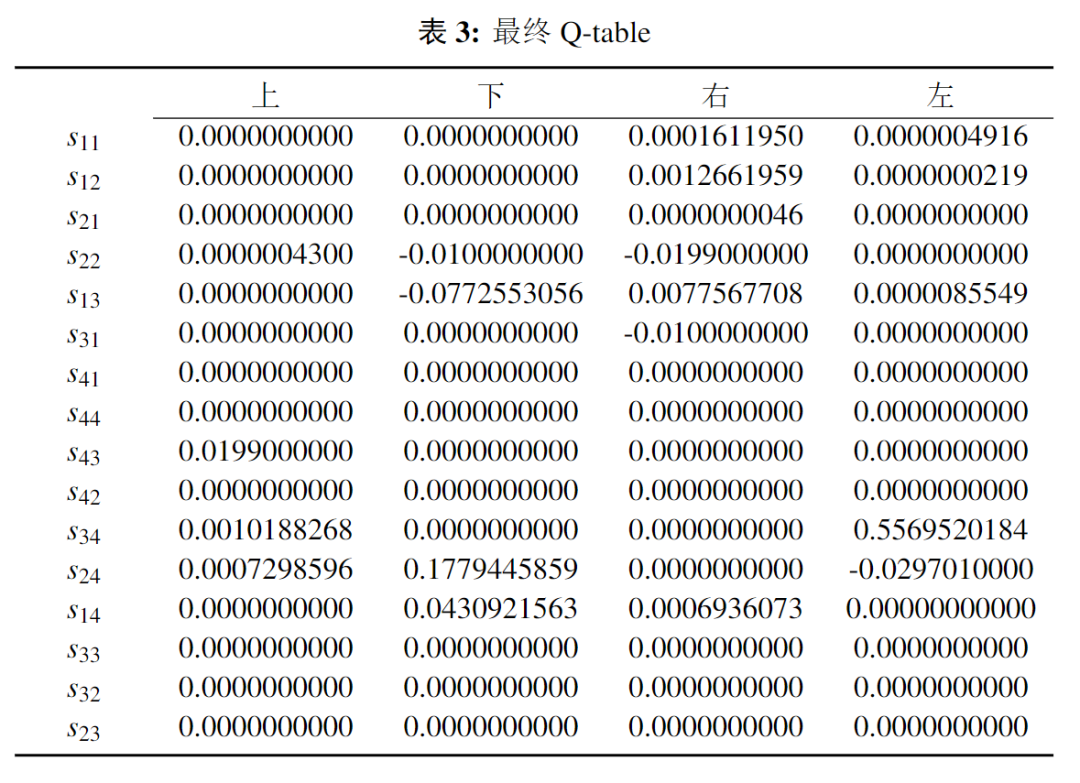
如图12所示，经过智能体不断的尝试、Q-table 的不断更新，智能体能够躲开陷阱以最短的步数找到宝藏。一段时间后，Q-table 到达收敛状态，可以看出图13中通往宝藏的状态-动作值为正值，而通往陷阱的状态-动作值为负值，因此此时智能体在进行决策时会更快更准确的通往宝藏。
6. 总结
马尔可夫过程作为一种重要的随机过程，在计算数学、金融经济、生物、化学、管理科学乃至人文科学中都有广泛的应用，马尔可夫链是马尔可夫过程的特例。本文首先基于《随机过程》课程中所学马尔可夫链的相关知识进行推广，介绍了强化学习中重要的模型——马尔可夫决策过程。其次对比分析了强化学习中求解马尔可夫决策环境的两种经典算法 Q-learning 和 Sarsa。最后，笔者以Q-learning算法为例，使用 Python 语言搭建了一个智能迷宫强化学习环境，使智能体在迷宫中通过不断的探索及试错，最终能够避开陷阱找到通往宝藏的最佳路径。实验结果表明智能体在环境中学习时长较短、学习效果良好。综上所述，笔者展示了马尔科夫链在强化学习中的实际应用。
参考文献
Code
#### 搭建可视化环境 ####
import numpy as np
import time
import sys
if sys.version_info.major == 2:
import Tkinter as tk
else:
import tkinter as tk
UNIT = 40 # pixels
MAZE_H = 4 # grid height
MAZE_W = 4 # grid width
class Maze(tk.Tk, object):
def __init__(self):
super(Maze, self).__init__()
self.action_space = ['u', 'd', 'l', 'r']
self.n_actions = len(self.action_space)
self.title('maze')
self.geometry('{0}x{1}'.format(MAZE_H * UNIT, MAZE_H * UNIT))
self._build_maze()
def _build_maze(self):
self.canvas = tk.Canvas(self, bg='white',
height=MAZE_H * UNIT,
width=MAZE_W * UNIT)
# create grids
for c in range(0, MAZE_W * UNIT, UNIT):
x0, y0, x1, y1 = c, 0, c, MAZE_H * UNIT
self.canvas.create_line(x0, y0, x1, y1)
for r in range(0, MAZE_H * UNIT, UNIT):
x0, y0, x1, y1 = 0, r, MAZE_W * UNIT, r
self.canvas.create_line(x0, y0, x1, y1)
# create origin
origin = np.array([20, 20])
# hell
hell1_center = origin + np.array([UNIT * 2, UNIT])
self.hell1 = self.canvas.create_rectangle(
hell1_center[0] - 15, hell1_center[1] - 15,
hell1_center[0] + 15, hell1_center[1] + 15,
fill='black')
# hell
hell2_center = origin + np.array([UNIT, UNIT * 2])
self.hell2 = self.canvas.create_rectangle(
hell2_center[0] - 15, hell2_center[1] - 15,
hell2_center[0] + 15, hell2_center[1] + 15,
fill='black')
# create oval
oval_center = origin + UNIT * 2
self.oval = self.canvas.create_oval(
oval_center[0] - 15, oval_center[1] - 15,
oval_center[0] + 15, oval_center[1] + 15,
fill='yellow')
# create red rect
self.rect = self.canvas.create_rectangle(
origin[0] - 15, origin[1] - 15,
origin[0] + 15, origin[1] + 15,
fill='red')
# pack all
self.canvas.pack()
def reset(self):
self.update()
time.sleep(0.5)
self.canvas.delete(self.rect)
origin = np.array([20, 20])
self.rect = self.canvas.create_rectangle(
origin[0] - 15, origin[1] - 15,
origin[0] + 15, origin[1] + 15,
fill='red')
# return observation
return self.canvas.coords(self.rect)
def step(self, action):
s = self.canvas.coords(self.rect)
base_action = np.array([0, 0])
if action == 0: # up
if s[1] > UNIT:
base_action[1] -= UNIT
elif action == 1: # down
if s[1] < (MAZE_H - 1) * UNIT:
base_action[1] += UNIT
elif action == 2: # right
if s[0] < (MAZE_W - 1) * UNIT:
base_action[0] += UNIT
elif action == 3: # left
if s[0] > UNIT:
base_action[0] -= UNIT
self.canvas.move(self.rect, base_action[0], base_action[1]) # move agent
s_ = self.canvas.coords(self.rect) # next state
# reward function
if s_ == self.canvas.coords(self.oval):
reward = 1
done = True
s_ = 'terminal'
elif s_ in [self.canvas.coords(self.hell1), self.canvas.coords(self.hell2)]:
reward = -1
done = True
s_ = 'terminal'
else:
reward = 0
done = False
return s_, reward, done
def render(self):
time.sleep(0.1)
self.update()
def update():
for t in range(10):
s = env.reset()
while True:
env.render()
a = 1
s, r, done = env.step(a)
if done:
break
if __name__ == '__main__':
env = Maze()
env.after(100, update)
env.mainloop()
#### 强化学习主体代码 ####
class QLearningTable:
def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
self.actions = actions # a list
self.lr = learning_rate
self.gamma = reward_decay
self.epsilon = e_greedy
self.q_table = pd.DataFrame(columns=self.actions, dtype=np.float64)
def choose_action(self, observation):
self.check_state_exist(observation)
# action selection
if np.random.uniform() < self.epsilon:
# choose best action
state_action = self.q_table.loc[observation, :]
# some actions may have the same value, randomly choose on in these actions
action = np.random.choice(state_action[state_action == np.max(state_action)].index)
else:
# choose random action
action = np.random.choice(self.actions)
return action
def learn(self, s, a, r, s_):
self.check_state_exist(s_)
q_predict = self.q_table.loc[s, a]
if s_ != 'terminal':
q_target = r + self.gamma * self.q_table.loc[s_, :].max() # next state is not terminal
else:
q_target = r # next state is terminal
self.q_table.loc[s, a] += self.lr * (q_target - q_predict) # update
def check_state_exist(self, state):
if state not in self.q_table.index:
# append new state to q table
self.q_table = self.q_table.append(
pd.Series(
[0]*len(self.actions),
index=self.q_table.columns,
name=state,
)
)
print(self.q_table)
#### 智能体学习实现 ####
from maze_env import Maze
from RL_brain import QLearningTable
def update():
for episode in range(100):
# initial observation
observation = env.reset()
while True:
# fresh env
env.render()
# RL choose action based on observation
action = RL.choose_action(str(observation))
# RL take action and get next observation and reward
observation_, reward, done = env.step(action)
# RL learn from this transition
RL.learn(str(observation), action, reward, str(observation_))
# swap observation
observation = observation_
# break while loop when end of this episode
if done:
break
# end of game
print('game over')
env.destroy()
if __name__ == "__main__":
env = Maze()
RL = QLearningTable(actions=list(range(env.n_actions)))
env.after(100, update)
env.mainloop()
