Merkle树结构
Merkle (默克尔)树,又叫哈希树,是一种典型的二叉树结构,由一个根节点 、一组中间节点和一组叶节点组成。在区块链系统出现之前,广泛用于文件系统和 P2P 系统中,如图 5-3 所示:
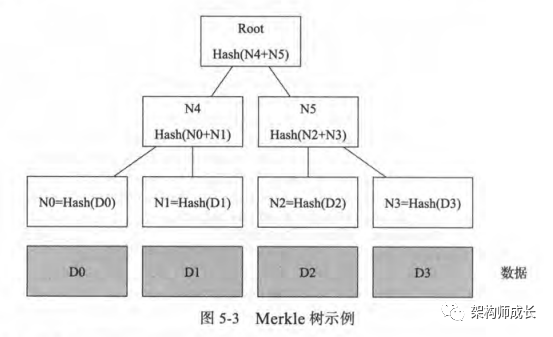
其主要特点为:
最下面的叶节点包含存储数据或其哈希值;
非叶子节点(包括中间节点和根节点)都是它的两个孩子节点内容的哈希值。
进一步地,默克尔树可以推广到多叉树的情形,此时非叶子节点的内容为它所有的孩子节点内容的哈希值。默克尔树逐层记录哈希值的特点,让它具有了一些独特的性质。例如,底层数据的任何变动,都会传递到其父节点,一层层沿着路径一直到树根。这意味树根的值实际上代表了对底层所有数据的“数字摘要”。
Merkle树应用场景
1. 快速比较大量数据
对每组数据排序后构建默克尔树结构。当两个默克尔树根相同时,则意味着两组数据必然相同。否则,必然存在不同。由于Hash计算的过程可以十分快速,预处理可以在短时间内完成。利用默克尔树结构能带来巨大的比较性能优势。
2. 快速定位修改
例如图 5-3 中,如果 D1 中数据被修改,会影响到N1、N4和Root。因此,一旦发现某个节点如Root 的数值发生变化,沿着 Root->N4->N1,最多通过O(lgn )时间即可快速定位到实际发生改变的数据块D1。
3. 零知识证明
零知识证明( zero knowledge proof)是这样的一个过程,证明者在不向验证者提供任何额外信息的前提下,使验证者相信某个论断是正确的。
仍以图 5-3 为例,如何向他人证明拥有的某组数据( D0···D3 )中包括给定某个内容D0而不暴露其他任何内容。
很简单,构造如图所示的一个默克尔树,公布N1、N5、Root。D0 拥有者通过验证生成的 Root 是否跟提供的值一致,即可很容易检测D0存在。整个过程中验证者无法获知其他内容。
零知识证明,目前一般认为至少要满足三个条件:
完整性( Completeness ):真实的证明可以让验证者成功验证;
可靠性( Soundness ):虚假的证明无法让验证者保证通过验证,但允许存在小概率例外;
零知识( Zero-Knowledge ):如果得到证明,无法从证明过程中获知除了所证明信息之外的任何信息。






