树中的概念
节点的度:结点拥有的子树数目称为结点的度。
节点关系:结点子树的根结点为该结点的孩子结点,相应该结点称为孩子结点的双亲结点,同一个双亲结点的孩子结点之间互称兄弟结点。
结点层次:从根开始定义起,根为第一层,根的孩子为第二层,以此类推。
树的深度:树中结点的最大层次数称为树的深度或高度。
二叉树
二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。
特点:
每个结点最多有两棵子树,即二叉树不存在度大于2的结点;
二叉树的子树有左右之分,其子树的次序不能颠倒;
即使树中某结点只有一棵子树,也要区分它是左子树还是右子树。
二叉树是递归定义的,其结点有左右子树之分,逻辑上二叉树有五种基本形态:

二叉树性质
1. 二叉树中如果深度为k,那么最多有2k-1个节点(k>=1)。
2. 在二叉树的第i层上最多有2i-1 个节点(i>=1)。
3. n0=n2+1 n0表示度数为0的节点数,n2表示度数为2的节点数。
4. 在完全二叉树中,具有n个节点的完全二叉树的深度为[log2n]+1,其中[log2n]是向下取整。
5. 若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号,则对完全二叉树中任意一个编号为 i 的结点有如下特性:
若 i=1,则该结点是二叉树的根,无双亲;否则,编号为 [i/2] 的结点为其双亲结点;
若 2i>n,则该结点无左孩子;否则,编号为 2i 的结点为其左孩子结点;
若 2i+1>n,则该结点无右孩子结点;否则,编号为2i+1 的结点为其右孩子结点。
满二叉树
满二叉树是除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。假设满二叉树深度为k,那么且有2^k-1个结点。
满二叉树的特点:
子只能出现在最下一层,出现在其它层就不可能达成平衡。
非叶子结点的度一定是2。
在同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多。
深度为3的满二叉树如下:
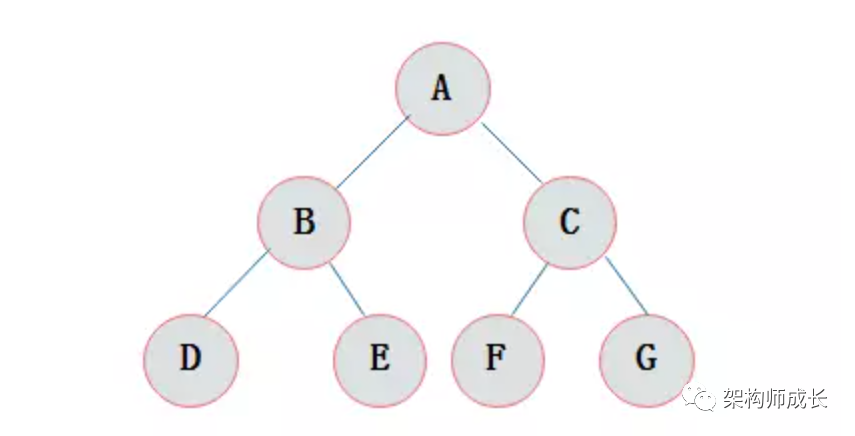
完全二叉树
对一颗具有n个结点的二叉树按层编号,如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树。满二叉树是一颗完全二叉树,但是完全二叉树不一定是满二叉树。
完全二叉树特点:
叶子结点只能出现在最下层和次下层。
最下层的叶子结点集中在树的左部。
倒数第二层若存在叶子结点,一定在右部连续位置。
如果结点度为1,则该结点只有左孩子,即没有右子树。
同样结点数目的二叉树,完全二叉树深度最小。
深度为3的完全二叉树如下:

二叉搜索树
二叉搜索树(Binary Search Tree),(也称为二叉查找树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树:
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
左、右子树也分别为二叉搜索树。
二叉搜索树作为一种经典的数据结构,它既有链表的快速插入与删除操作的特点,又有数组快速查找的优势;所以应用十分广泛,例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。二叉搜索树的查找效率取决于树的高度,因此保持树的高度最小,即可保证树的查找效率。
如下图是一颗二叉搜索树:
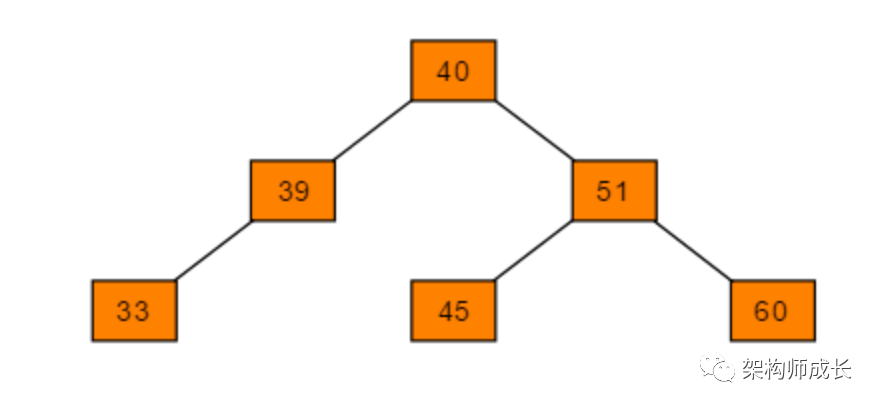
平衡二叉树
平衡二叉树又被称为AVL树(区别于AVL算法),它是一棵二叉排序树,且具有以下性质:
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1;
左右两个子树都是一棵平衡二叉树。
二叉搜索树一定程度上可以提高搜索效率,但是当原序列有序,例如序列A = {1,2,3,4,5,6},构造二叉搜索树如下图。依据此序列构造的二叉搜索树为右斜树,同时二叉树退化成单链表,搜索效率降低为O(n)。
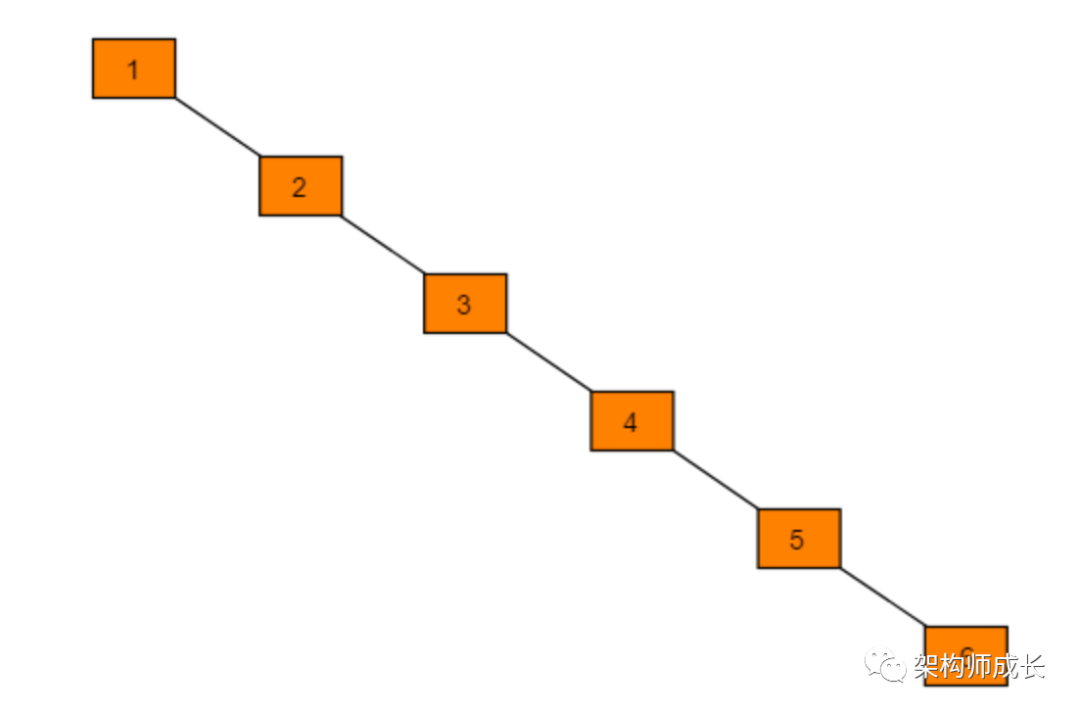
在此二叉搜索树中查找元素6需要查找6次。二叉搜索树的查找效率取决于树的高度,因此保持树的高度最小,即可保证树的查找效率。同样的序列A,改为下图式存储,查找元素6时只需比较3次,查找效率提升一倍。
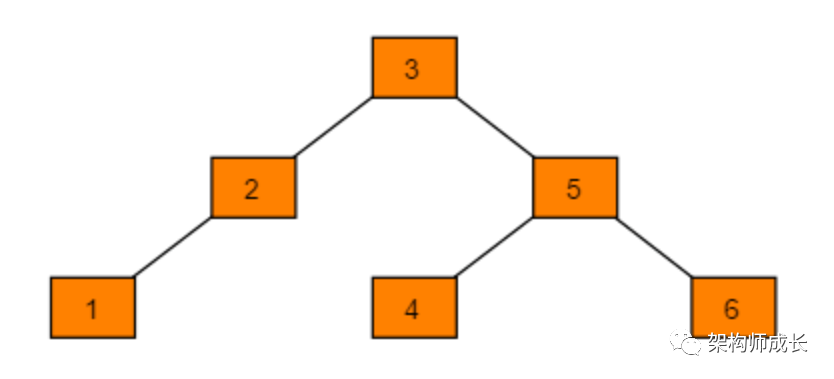
可以看出当节点数目一定,保持树的左右两端保持平衡,树的查找效率最高。这种左右子树的高度相差不超过1的树为平衡二叉树。
哈夫曼树
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
术语:
路径和路径长度:在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
结点的权及带权路径长度:若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
树的带权路径长度:树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL。
构造哈夫曼树
假设有n个权值,则构造出的哈夫曼树有n个叶子结点。n个权值分别设为 w1、w2、…、wn,则哈夫曼树的构造规则为:
(1) 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点);
(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3)从森林中删除选取的两棵树,并将新树加入森林;
(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。
假设有a:7,b:5,c:2,d:4 总共4个节点,构造哈夫曼树的过程如下:
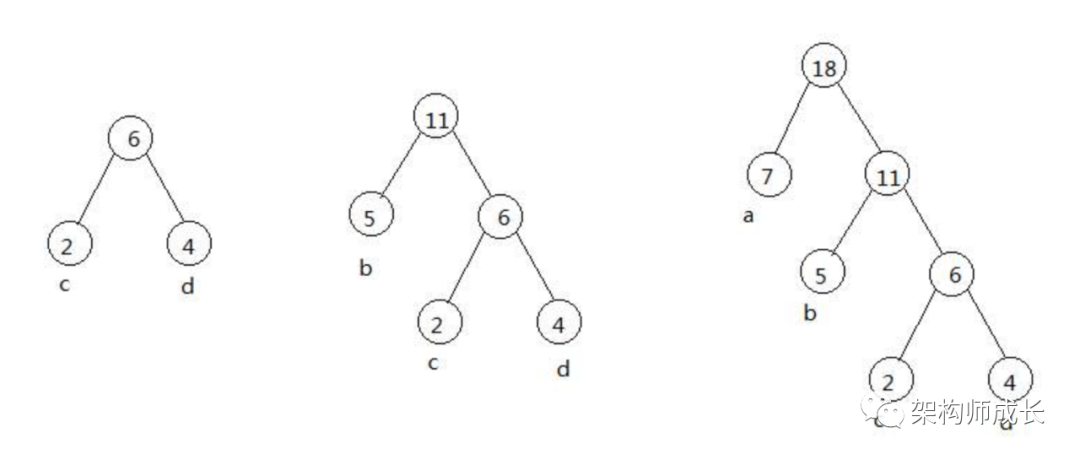
哈夫曼树编码
构造出霍夫曼树后,对霍夫曼树执行遍历。将向左子树路径标记为0,向右子树的路径标记为1。如下图:
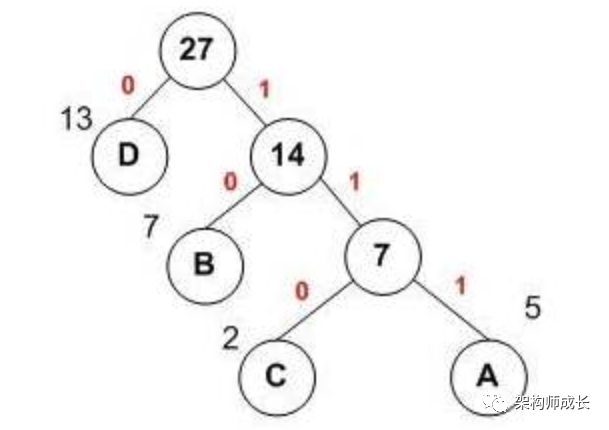
A、B、C、D对应的编码为:111、10、110、0。
使用霍夫曼编码可以缩短数据编码长度,达到数据压缩的效果。当字符数目较少时不能体现霍夫曼编码带来的压缩效果,但是当字符数目较多时,霍夫曼编码的压缩效率将显著提高。
红黑树
红黑树是一棵二叉搜索树,它在每个节点增加了一个存储位记录节点的颜色,可以是RED,也可以是BLACK;通过任意一条从根到叶子简单路径上颜色的约束,红黑树保证最长路径不超过最短路径的二倍,因而近似平衡。
红黑树具有以下性质:
每个节点颜色不是黑色,就是红色;
根节点是黑色的;
如果一个节点是红色,那么它的两个子节点就是黑色的(没有连续的红节点);
对于每个节点,从该节点到其后代叶节点的简单路径上,均包含相同数目的黑色节点。
红黑树插入、删除等按照二叉搜索树方式,插入后再根据红黑树规则进行旋转,调整。一颗红黑树如下:
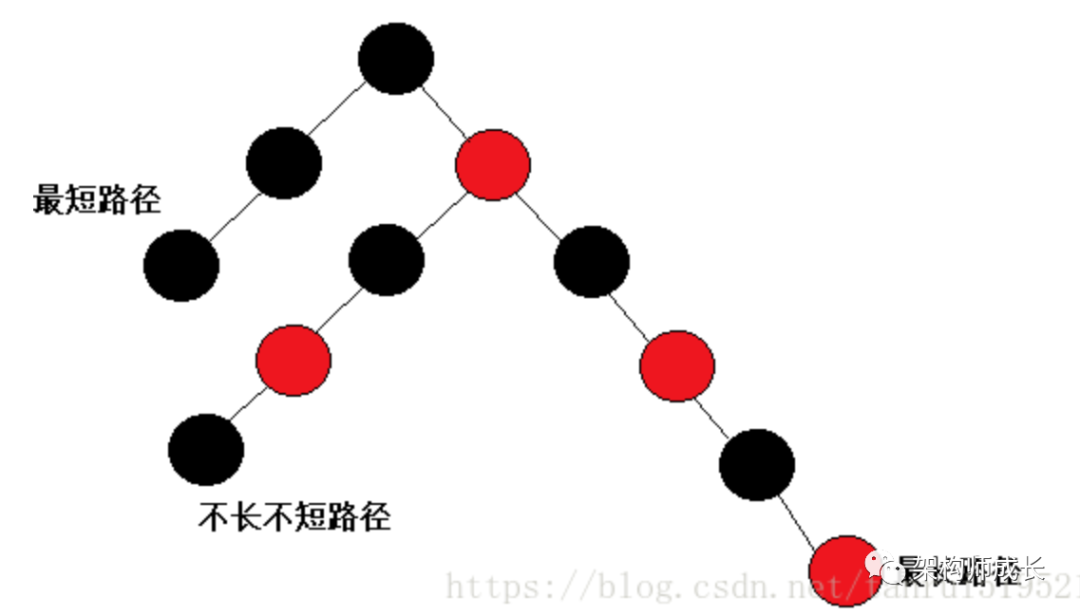
红黑树和平衡二叉搜索树对比:
1. AVL树的时间复杂度虽然优于红黑树,但是对于现在的计算机,cpu太快,可以忽略性能差异。
2. 红黑树的插入删除比AVL树更便于控制操作。
3. 红黑树整体性能略优于AVL树(红黑树旋转情况少于AVL树)。
4. 平衡树(AVL)是为了解决 二叉查找树(BST)退化为链表的情况。
5. 红黑树(RBT)是为了解决 平衡树 在删除等操作需要频繁调整的情况。
6. 和红黑树相比,AVL是严格的平衡二叉树,平衡条件必须满足所有节点左右子树高度不超过1。
平衡二叉树最大的作用就是查找,AVL树的查找、插入和删除在平均和最坏情况下时间复杂度都是O(logn)。AVL平衡树适用于插入、删除比较少的情况,查找比较多的情况。
红黑树总保持黑色完美平衡,所以它的查找最坏时间复杂度为O(2lgN)。红黑树红黑树的时间复杂度平均为O(logn)。红黑树是一种弱平衡二叉树(由于是弱平衡,可以看到,在相同节点情况下,AVL树的高度低于红黑树),相对于严格的AVL树来说,它的旋转次数较少,所以对于搜索,插入,删除操作较多的情况下,我们就用红黑树。
红黑树构建过程
参考:
https://zhuanlan.zhihu.com/p/79980618?utm_source=cn.wiz.note
红黑树应用
广泛应用于C++的STL中,地图和集都是用红黑树实现的。
LINUX的进程调度完全公平调度程序,用红黑树管理进程控制块,进程的虚拟内存区域都存储在一棵红黑树上,每个虚拟地址区域都对应红黑树的一个节点,左指针指向相邻的地址虚拟存储区域,右指针指向相邻的高地址虚拟地址空间。
IO多路复用的epoll的实现采用红黑树组织管理的sockfd,以支持快速的增删改查。
Nginx中用红黑树管理定时器,因为红黑树是有序的,可以很快的得到距离当前最小的定时器。
Java TreeMap红黑树实现。根据其键的自然顺序进行排序,或者根据创建映射时提供的 Comparator 进行排序,具体取决于使用的构造方法。
二叉树的关系
以上二叉树,包含范围如下:
二叉树>完全二叉树>满二叉树
二叉树>二叉搜索树>平衡二叉树
二叉树>二叉搜索树>红黑树
二叉树>哈夫曼树
参考:
https://www.jianshu.com/p/bf73c8d50dc2
https://xiaozhuanlan.com/topic/2937850641






