遍历方式
二叉树深度优先遍历方式有先序遍历、中序遍历、后序遍历。
假设树形结构如下:
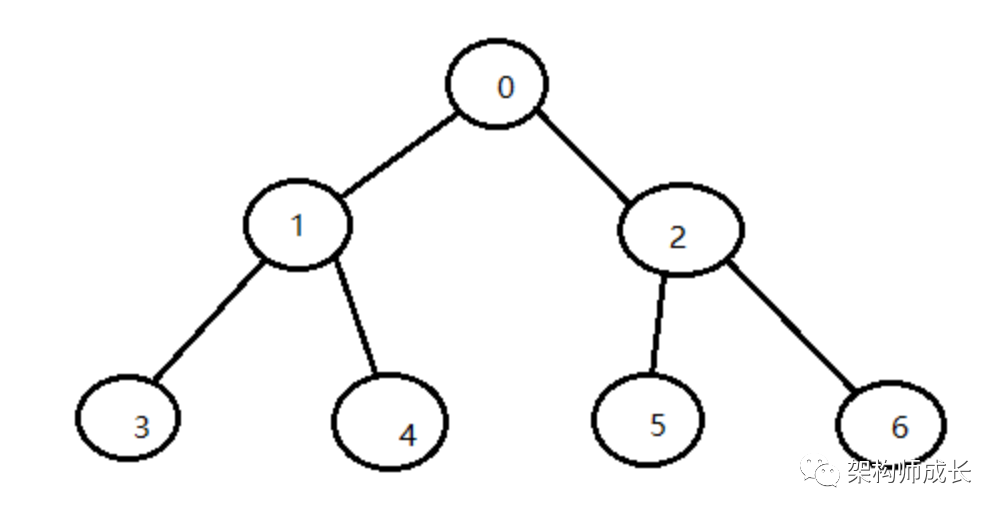
深度优先遍历实现
import java.util.ArrayList;import java.util.List;public class BinaryTreeTraverse {static class BinTree {public BinTree left;public BinTree right;public BinTree root;// 数据域private Object data;// 存节点public List<BinTree> datas;public BinTree(BinTree left, BinTree right, Object data) {this.left = left;this.right = right;this.data = data;}// 将初始的左右孩子值为空public BinTree(Object data) {this(null, null, data);}public BinTree() {}public void createTree(Object[] objs) {datas = new ArrayList<BinTree>();// 将一个数组的值依次转换为Node节点for (Object o : objs) {datas.add(new BinTree(o));}// 第一个数为根节点root = datas.get(0);// 建立二叉树for (int i = 0; i < objs.length / 2; i++) {//左孩子datas.get(i).left = datas.get(i * 2 + 1);// 右孩子if (i * 2 + 2 < datas.size()) {//避免偶数的时候 下标越界datas.get(i).right = datas.get(i * 2 + 2);}}}//先序遍历public void preOrder(BinTree root) {if (root != null) {System.out.print(root.data + " ");preOrder(root.left);preOrder(root.right);}}//中序遍历public void inOrder(BinTree root) {if (root != null) {inOrder(root.left);System.out.print(root.data+ " ");inOrder(root.right);}}//后序遍历public void afterOrder(BinTree root) {if (root != null) {afterOrder(root.left);afterOrder(root.right);System.out.print(root.data+ " ");}}}public static void main(String[] args) {BinTree BinTree = new BinTree();Object[] a = {0,1, 2, 3, 4, 5, 6};BinTree.createTree(a);System.out.print("先序遍历:");BinTree.preOrder(BinTree.root);System.out.println();System.out.print("中序遍历:");BinTree.inOrder(BinTree.root);System.out.println();System.out.print("后序遍历:");BinTree.afterOrder(BinTree.root);}}
实现结果:
先序遍历:0 1 3 4 2 5 6中序遍历:3 1 4 0 5 2 6后序遍历:3 4 1 5 6 2 0
文章转载自架构师成长,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






