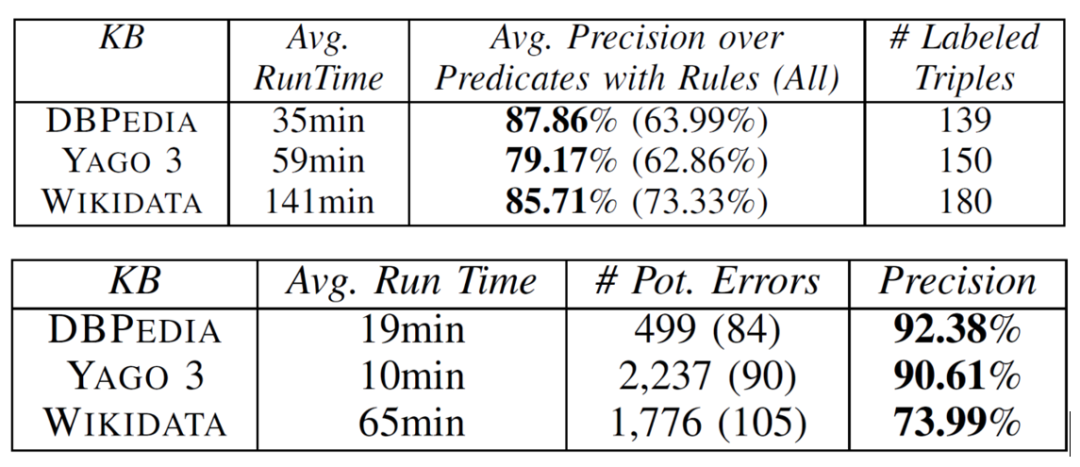
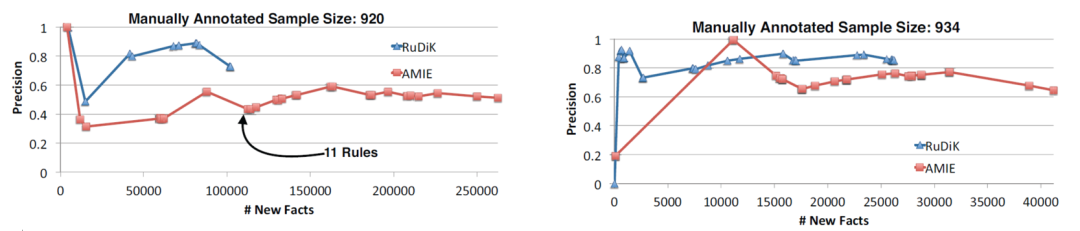
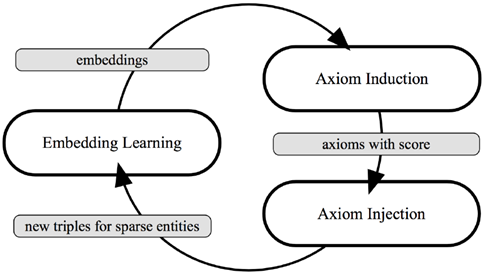
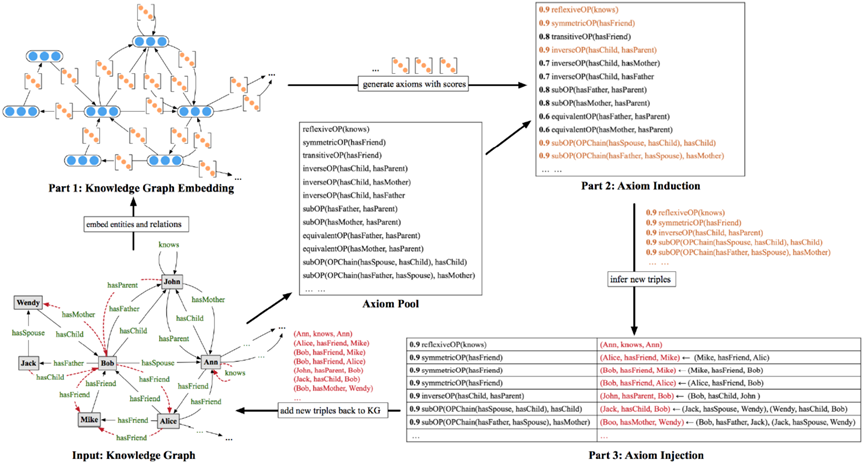
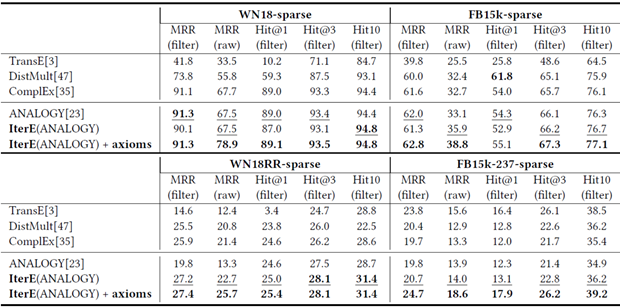
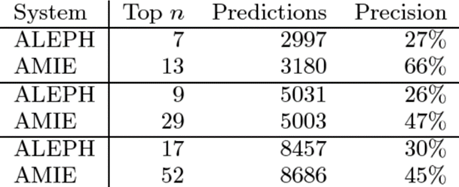
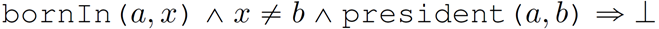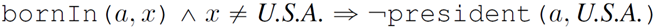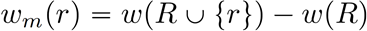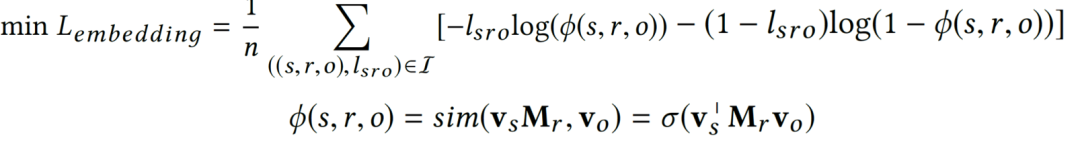面向知识图谱的规则挖掘研究对象是知识图谱上的一阶谓词逻辑规则,通常由body ⇒ head(规则体⇒规则头)的形式构成,规则体由多个原子的析取组成,规则头是包含目标谓词的单个原子,例如:知识图谱上的规则挖掘可以用来描述数据的一般规律,有助于理解数据,并在此基础上进行推理、补全、和检错纠错。本文将介绍三个面向知识图谱的规则挖掘方法:AMIE[1]是经典的规则挖掘模型,Rudik[2]和IterE[3]模型分别采用不同的思想在规则挖掘过程中引入实体、属性信息。接下来分别进行介绍。其中“连通”要求规则中每个原子通过共享变量或实体传递相连,“闭式”限定规则中每个变量都至少出现2次。规则挖掘的最朴素算法是枚举所有可能的规则,但该方法搜索空间大,不适用于大规模知识图谱。本文的主要思想是采用三个挖掘操作算子迭代地扩展规则,同时定义多个标准对规则进行评估和剪枝。三个挖掘操作算子为:1)添加悬挂边:边的一端是一个未出现过的变量,另一端(变量/常量)在规则中出现过;2)添加实例边:边的一端在规则中出现过的常量/变量,另一端是未出现过的常量,即知识图谱中的实体;3)添加闭合边:连接两个已存在于规则中的常量/变量的边。在规则挖掘的同时,本文定义了多个标准对规则质量进行评估:以上标准置信度中,前提是将知识图谱中出现的元组认为是正确信息,未出现的元组认为是错误信息,这不符合知识图谱的开放世界假设。为了解决这一问题,本文提出了部分完整性假设(partial completeness assumption, PCA),认为如果存在某个实体x的关系r属性, 则知识库中包含了x的所有关系r属性。由此提出了PCA置信度。该算法的输入是整个知识图谱k,以及超参数:最小头覆盖度、最大规则长度、最小置信度。第2行将候选规则队列初始化为目标谓词相关三元组作为规则头的空规则。第3行将输出集合初始化为空。第4行至第17行迭代对候选规则进行扩展、评估、剪枝。第6行判断当前出队的规则是够满足输出要求(规则为闭式规则,置信度大于最小置信度,以及置信度大于比其少一个原子的规则置信度),若满足则加入输出集合。第10行继续将不满足输出要求的规则进行扩展。本文将所提模型AMIE与两个已有模型进行了比较,在YAGO2 sample数据集上,AMIE挖掘出207条符合要求的规则,而WARMR仅挖掘出41条;在YAGO2数据集上,AMIE挖掘出335条符合要求的规则,而WARMR仅挖掘出56条。与WARMR模型的预测结果比较可以得出本文模型挖掘出的规则预测结果精确度更高。此外,本文模型还在其他知识图谱进行了实验,结果见下表:在DBpedia上挖掘的规则数量多于YAGO,原因是DBpedia上的关系更多。本文的目标同样是挖掘连通、闭式的霍恩规则,与AMIE方法不同的是,本文挖掘出的规则还包括负规则,即包含否定表述的规则,另外还引入了数字、日期等属性值的比较和实体间的比较。例如:本文研究的问题可以定义为:给定知识图谱kb,针对目标谓词的生成集G,验证集V,kb上的所有有效霍恩规则集R,及规则对应的权重。目标是搜索规则子集R’,使规则集权重最小。规则的权重越小则质量越高,权重为0表示规则完全覆盖G,且不覆盖V。验证集V:不符合目标谓词的实体对。由于知识图谱的开放世界假设,构造验证集数据不能采用随机采样的方法。本文根据封闭世界假设(给定主语和谓词,若KG中包含一个或多个宾语,则它已包含所有可能的值)通过以下方法进行构造:(x,y)之间有相连谓词,但不是目标谓词,且x或y有目标谓词相连,另一端不是y或x。注意挖掘负规则时方法不变,将生成集和验证集的数据对换即可。给定目标谓词相关的生成集、验证集后,则可以在此基础上进行候选规则生成。本文的基本思想是连通的规则体可以翻译为一段路径。于是用过以下标准查询符合要求的路径来构造候选规则:3)在x/y/已访问过的其他顶点结束(长度小于最长路径长度限制)。另外值得注意的是,本文在规则挖掘时引入了五个特殊关系,使规则中包含属性值、实体的比较信息,具体处理如下:1)增加特殊关系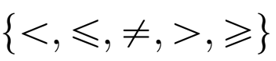 ,在样本图中比较数字、日期之间大小关系,比较字符串之间的≠关系;2)同一样本图中,添加相同type的实体之间的≠关系;规则举例:3)常量替换。当且仅当对G中被r覆盖的每对(x,y),其中v都能被实例化为同一实体e,则用e替代变量v。规则举例:构造出所有候选规则后,接下来要对规则进行选择。本文定义了规则的边际权重,以此为依据对规则进行选择:本文采用贪婪策略进行算法选择,给定生成集G,验证集V,所有候选规则集R,每次迭代选择最小边际权重的规则添加到R’。迭代的终止条件为:最后,受A*算法的启发,本文定义了对规则边际权重的估计方法,无需生成所有候选规则,在路径扩展过程中每次选择最有希望的路径。总体算法如下:本文在DBpedia,YAGO3,WikiData上进行了实验,分别挖掘正、负规则情况见下表:本文方法与AMIE模型在YAGO和DBpedia数据集上挖掘的正规则预测结果见下图:从实验结果可以得出,虽然本文挖掘规则的数量比AMIE模型更少,但预测结果的精确率上优势明显。文章三:面向知识图谱推理的迭代知识表示学习和规则学习本文挖掘的目标是本体公理,作者选取了七条与对象属性相关的表达式公理,并将其转化为规则形式:本文认为规则推理方法准确性高,可解释性强,但搜索空间较大效率不高,知识表示推理方法扩展型强,效率更高,但在稀疏实体上学习效果较差。于是采用了迭代学习思想,二者互相补充。规则从知识表示中通过合理剪枝策略学得,知识表示从现有三元组及规则预测的三元组中学得。框架结构见下图:模块一:表示学习。表示学习模块采用现有的基于线性映射假设的方法。损失函数为:模块二:公理归纳,即通过关系表示归纳公理集合,并赋置信度。首先是候选公理生成,包含以下三步:1)生成公理or部分公理,用确定的关系作为规则头;2) 通过随机选择k个三元组来补全部分公理。选择关系r相连的三元组(e', r, e''),使用与e', e''直接相连的关系替换公理中的r', r'';3)计算每个公理的支持度,大于1则加入候选公理集。模块三:公理注入,即通过公理预测稀疏实体相关的新信息,将其用于下次迭代中的知识表示学习模块。预测结果的置信度为推理出该结果的公理对应的置信度:本文在四个稀疏数据集上进行了实验,并分别与基于知识表示的方法和基于规则挖掘的方法进行比较。与基于知识表示方法的结果见下表:可以得出,本文模型挖掘出规则进行链接预测的结果优于表示学习的方法,而且本文挖掘出的高质量规则,数量上也多于经典的规则挖掘模型AMIE+。面向知识图谱的规则挖掘方法,由于其规则可解释性强,准确性高等优点,持续受到广泛关注,但面临扩展性差,规则的复杂性及表达能力有限等问题。传统的规则通常只关注谓词之间的关系,从以上介绍的方法可以看出,实体及属性信息的合理运用,有助于增加规则表达的复杂性,优化规则搜索效率,因此具有较大研究价值。但目前在规则挖掘过程中对丰富的实体、属性等语义信息的使用还比较初步,有待进一步尝试和探索。
,在样本图中比较数字、日期之间大小关系,比较字符串之间的≠关系;2)同一样本图中,添加相同type的实体之间的≠关系;规则举例:3)常量替换。当且仅当对G中被r覆盖的每对(x,y),其中v都能被实例化为同一实体e,则用e替代变量v。规则举例:构造出所有候选规则后,接下来要对规则进行选择。本文定义了规则的边际权重,以此为依据对规则进行选择:本文采用贪婪策略进行算法选择,给定生成集G,验证集V,所有候选规则集R,每次迭代选择最小边际权重的规则添加到R’。迭代的终止条件为:最后,受A*算法的启发,本文定义了对规则边际权重的估计方法,无需生成所有候选规则,在路径扩展过程中每次选择最有希望的路径。总体算法如下:本文在DBpedia,YAGO3,WikiData上进行了实验,分别挖掘正、负规则情况见下表:本文方法与AMIE模型在YAGO和DBpedia数据集上挖掘的正规则预测结果见下图:从实验结果可以得出,虽然本文挖掘规则的数量比AMIE模型更少,但预测结果的精确率上优势明显。文章三:面向知识图谱推理的迭代知识表示学习和规则学习本文挖掘的目标是本体公理,作者选取了七条与对象属性相关的表达式公理,并将其转化为规则形式:本文认为规则推理方法准确性高,可解释性强,但搜索空间较大效率不高,知识表示推理方法扩展型强,效率更高,但在稀疏实体上学习效果较差。于是采用了迭代学习思想,二者互相补充。规则从知识表示中通过合理剪枝策略学得,知识表示从现有三元组及规则预测的三元组中学得。框架结构见下图:模块一:表示学习。表示学习模块采用现有的基于线性映射假设的方法。损失函数为:模块二:公理归纳,即通过关系表示归纳公理集合,并赋置信度。首先是候选公理生成,包含以下三步:1)生成公理or部分公理,用确定的关系作为规则头;2) 通过随机选择k个三元组来补全部分公理。选择关系r相连的三元组(e', r, e''),使用与e', e''直接相连的关系替换公理中的r', r'';3)计算每个公理的支持度,大于1则加入候选公理集。模块三:公理注入,即通过公理预测稀疏实体相关的新信息,将其用于下次迭代中的知识表示学习模块。预测结果的置信度为推理出该结果的公理对应的置信度:本文在四个稀疏数据集上进行了实验,并分别与基于知识表示的方法和基于规则挖掘的方法进行比较。与基于知识表示方法的结果见下表:可以得出,本文模型挖掘出规则进行链接预测的结果优于表示学习的方法,而且本文挖掘出的高质量规则,数量上也多于经典的规则挖掘模型AMIE+。面向知识图谱的规则挖掘方法,由于其规则可解释性强,准确性高等优点,持续受到广泛关注,但面临扩展性差,规则的复杂性及表达能力有限等问题。传统的规则通常只关注谓词之间的关系,从以上介绍的方法可以看出,实体及属性信息的合理运用,有助于增加规则表达的复杂性,优化规则搜索效率,因此具有较大研究价值。但目前在规则挖掘过程中对丰富的实体、属性等语义信息的使用还比较初步,有待进一步尝试和探索。[1] Galárraga,Luis Antonio, et al. "AMIE: association rule mining under incompleteevidence in ontological knowledge bases." Proceedings of the 22ndinternational conference on World Wide Web. 2013.
[2] Ortona,Stefano, Venkata Vamsikrishna Meduri, and Paolo Papotti. "Rudik: Rulediscovery in knowledge bases." Proceedings of the VLDB Endowment 11.12(2018): 1946-1949.
[3] Zhang,Wen, et al. "Iteratively learning embeddings and rules for knowledgegraph reasoning." The World Wide Web Conference. 2019.
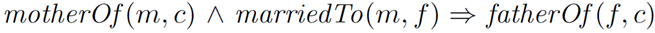



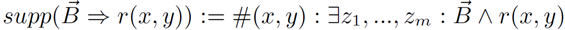
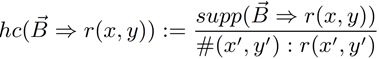
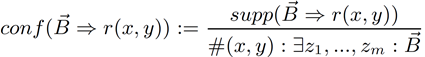
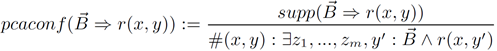





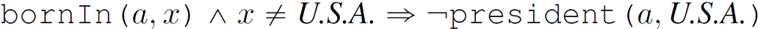
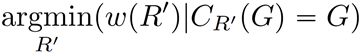
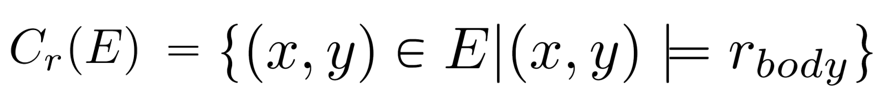
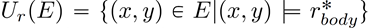
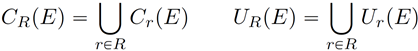
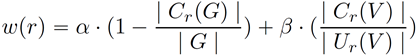
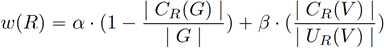
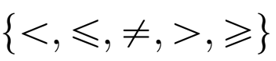 ,在样本图中比较数字、日期之间大小关系,比较字符串之间的≠关系;
,在样本图中比较数字、日期之间大小关系,比较字符串之间的≠关系;