一、线段树介绍
线段树(Segment Tree), 是一种 二叉搜索树。区别在于线段树的每一个节点记录的都是一个区间. 每个区都被平均分为2个子区间,称为左子树和右子树.
比如说区间[0, 9], 一共10个元素, 每个子节点的区间元素个数都是父节点的元素个数一半, 若出现 奇数 的情况, 则 右子树 元素区间 比 左子树 区间多一个.
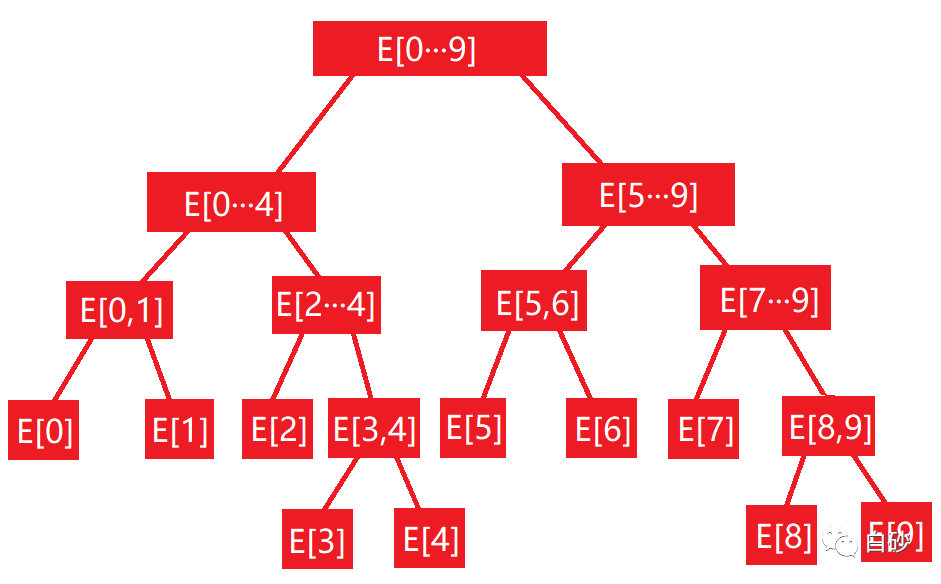
如果我们构建一个线段树区间, 数组的空间大小应该是多少呢?
假设我们把 线段树 看做是一颗 满二叉树,并且不考虑添加元素的情况(即区间固定)
| 层数 | 个数 |
| 0层 | 1 |
| 1层 | 2 |
| 2层 | 4 |
| 3层 | 8 |
| ... | ... |
| h-1层 | 2^(h-1) |
下层节点数是上层的节点数量 2倍, 最后一层的节点数, 大致等于前面所有层节点之和.
对于区间有 n 个元素的数组若 n=2^k(k是正整数) 则需要 2n 的空间,最差的情况是若 n=2^k+1 则需要 4n 的空间
如下图所示,最下面一层没有元素的节点使用 null 填充:
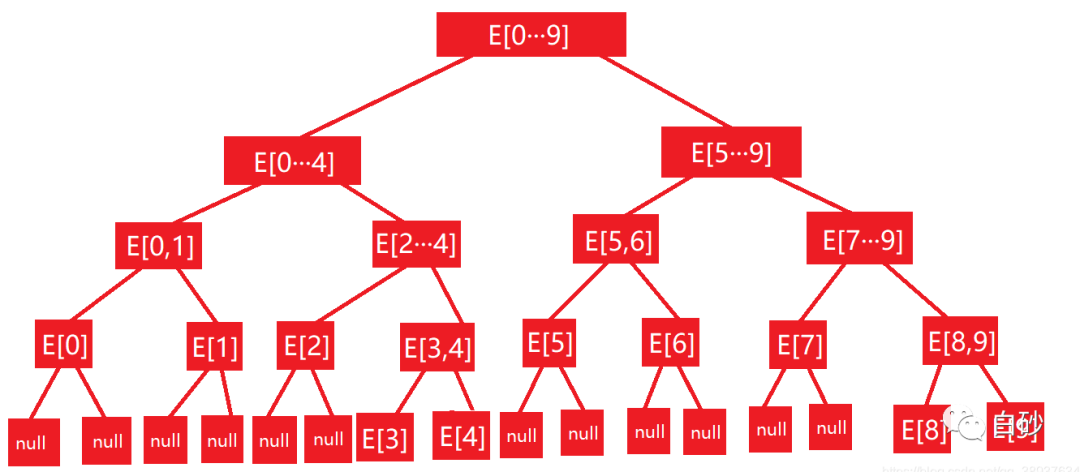
若索引是从 i=0 开始的,左儿子 left(i) = 2*i+1,右儿子 right(i) = 2*i+2,parent(i) = (i-1)/2 取整;
<?php
/**
* Created by : PhpStorm
* User: think abel
* Date: 2021/1/23 0023
* Time: 14:40
*/
class SegmentTree
{
/**
* @var array 用户传递的数组值
*/
private $data = [];
/**
* @var int 当前数组大小
*/
private $size;
/**
* @var array 线段树
*/
private $tree = [];
public function __construct($arr)
{
$this->size = count($arr);
for ($i = 0; $i < $this->size; $i ++) {
$this->data[$i] = $arr[$i];
}
/**
* 一个线段树当做满二叉树 需要使用4n的空间存储
* 这里php语言有限
*/
$this->buildSegmentTree(0, 0, $this->size - 1);
}
/**
* Notes: 在 treeIndex 的 位置 创建 表示区间 [left...right]的线段树
* User: think abel
* Date: 2021/1/23 0023
* Time: 14:54
*
* @param int $treeIndex treeIndex的索引
* @param int $left 对于根节点所表示的区间左端点
* @param int $right 对于根节点所表示的区间右端点
*/
private function buildSegmentTree(int $treeIndex, int $left, int $right)
{
/*
* 如果左端点 等于 右端点, 就是说左端点已经到了整个数组的最后一个
* 叶子结点里存的信息就是本身整个数组的最后一个元素
*/
if ($left === $right) {
$this->tree[$treeIndex] = $this->data[$left];
}
else {
$leftTreeIndex = $this->leftChild($treeIndex);
$rightTreeIndex = $this->rightChild($treeIndex);
//求区间中值
$mid = $left + ceil(($right - $left) / 2);
//递归左子树
$this->buildSegmentTree($leftTreeIndex, $left, $mid - 1);
//递归右子树
$this->buildSegmentTree($rightTreeIndex, $mid, $right);
//这里是根据业务来定节点需要存储的元素
$this->tree[$treeIndex] = $this->tree[$leftTreeIndex] + $this->tree[$rightTreeIndex];
}
}
/**
* Notes: 获取一个值
* User: think abel
* Date: 2021/1/23 0023
* Time: 14:43
*
* @param $index
*
* @return mixed
* @throws Exception
*/
public function get($index)
{
if ($index < 0 || $index >= $this->size) {
throw new Exception("获取失败, index require >= 0 and < " . $this->size);
}
return $this->data[$index];
}
/**
* Notes: 返回 左右 区间的值
* User: think abel
* Date: 2021/1/23 0023
* Time: 16:02
*
* @param $left
* @param $right
*
* @return mixed
*/
public function query($left, $right)
{
if ($left < 0 || $left >= $this->size
|| $right < 0
|| $right >= $this->size
|| $left > $right
) {
echo "index is illegal.";
die;
}
return $this->queryRecursion(0, 0, $this->size - 1, $left, $right);
}
/**
* Notes: 在以 treeIndex 为根节点的线段树中 [left...right]的范围里, 搜索区间[$queryLeft ... $queryRight]的值
* User: think abel
* Date: 2021/1/23 0023
* Time: 16:07
*
* @param $treeIndex
* @param $left
* @param $right
* @param $queryLeft
* @param $queryRight
*
* @return mixed
*/
private function queryRecursion($treeIndex, $left, $right, $queryLeft, $queryRight)
{
if ($left == $queryLeft && $right == $queryRight) {
return $this->tree[$treeIndex];
}
// 求区间中值向上取整
$mid = ceil($left + ($right - $left) / 2);
// treeIndex的节点分为[l...mid]和[mid+1...r]两部分
$leftTreeIndex = $this->leftChild($treeIndex);
$rightTreeIndex = $this->rightChild($treeIndex);
if ($queryLeft >= $mid) {
return $this->queryRecursion($rightTreeIndex, $mid, $right, $queryLeft, $queryRight);
}
elseif ($queryRight < $mid) {
return $this->queryRecursion($leftTreeIndex, $left, $mid - 1, $queryLeft, $queryRight);
}
$leftResult = $this->queryRecursion($leftTreeIndex, $left, $mid - 1, $queryLeft, $mid - 1);
$rightResult = $this->queryRecursion($rightTreeIndex, $mid, $right, $mid, $queryRight);
return $leftResult + $rightResult;
}
public function set($index, $e)
{
if ($index < 0 || $index >= $this->size) {
echo 'Index is illegal';
die;
}
// 更新数组值
$this->data[$index] = $e;
// 递归更新线段树中的值
$this->setRecursion(0, 0, $this->size - 1, $index, $e);
}
/**
* Notes: 在 treeIndex 为根的线段树中更新index的值为 e
* User: think abel
* Date: 2021/1/23 0023
* Time: 17:11
*
* @param $treeIndex
* @param $left
* @param $right
* @param $index
* @param $e
*
* @return mixed
*/
private function setRecursion($treeIndex, $left, $right, $index, $e)
{
/**
* 如果开始节点 == 整个线段树最后一个节点, 说明肯定是找到了这个元素
*/
if ($left == $right) {
$this->tree[$treeIndex] = $e;
}
else {
// 求区间中值向上取整
$mid = ceil($left + ($right - $left) / 2);
// treeIndex的节点分为[l...mid]和[mid+1...r]两部分
$leftTreeIndex = $this->leftChild($treeIndex);
$rightTreeIndex = $this->rightChild($treeIndex);
if ($index >= $mid) {
$this->setRecursion($rightTreeIndex, $mid, $right, $index, $e);
}
elseif ($index < $mid) {
$this->setRecursion($leftTreeIndex, $left, $mid - 1, $index, $e);
}
$this->tree[$treeIndex] = $leftTreeIndex + $rightTreeIndex;
}
}
/**
* Notes: 获取大小
* User: think abel
* Date: 2021/1/23 0023
* Time: 14:44
*
* @return int
*/
public function getSize()
{
return $this->size;
}
/**
* Notes: 返回左孩子的节点
* User: think abel
* Date: 2021/1/23 0023
* Time: 14:48
*
* @param int index
*
* @return int
*/
private function leftChild($index)
{
return 2 * $index + 1;
}
/**
* Notes: 返回右孩子的节点
* User: think abel
* Date: 2021/1/23 0023
* Time: 14:48
*
* @param int index
*
* @return int
*/
private function rightChild($index)
{
return 2 * $index + 2;
}
public function toString()
{
$str = '[';
for ($i = 0; $i < $this->size; $i ++) {
if ($this->tree[$i]) {
$str .= $this->tree[$i];
}
else {
$str .= null;
}
if ($i != $this->size - 1) {
$str .= ',';
}
}
$str .= ']';
return $str;
}
}
<?php
include "SegmentTree/SegmentTree.php";
$arr = [-2, 0, 3, -5, 2, -1];
$segTree = new SegmentTree($arr);
print_r($segTree);
echo $segTree->toString();
echo PHP_EOL;
echo $segTree->query(0,4);
$segTree->set(1, -1);
echo PHP_EOL;
echo $segTree->query(0,1);
print_r($segTree);