本文译自论文TinyLFU: A Highly Efficient Cache Admission Policy,地址:https://arxiv.org/pdf/1512.00727.pdf或http://www.cs.technion.ac.il/~gilga/TinyLFU_PDP2014.pdf,如无法下载可以私信给我索取。
前言
通过本文你能知道什么:
1.LFU分为两种,一种是维护所有访问频率信息的PLFU,另一种是维护在当前缓存中的key的频率访问信息的WLFU。PLFU效果最佳,但是维护的元数据成本开销较大。2.LFU的一个流行的替代方法依赖于时间局部性属性,这个替代方法称为“最近最少使用”(LRU)。与LFU相比,LRU的实现效率更高,可以自动适应数据访问模式的时间变化和工作负载的激增。然而,在许多工作负载下,为了获得相同的命中率,LRU需要比LFU大得多的缓存(因为无法保证缓存的命中率,低命中率的缓存也会在内存中存放较长时间)3.分段LRU (SLRU)[39]策略通过区分在短时间内至少访问两次的暂时流行项与在此期间只访问一次的项来捕获最近流行的情况。这一区别是通过两个固定大小的LRU段来管理缓存的,一个试用段(A1)和一个受保护段(A2)。4.reset机制:每当我们向近似图中添加一项时,我们就增加一个计数器。一旦这个计数器达到样本大小(W),我们将它和5近似图中的所有其他计数器除以2。5.TinyLFU采取了近似计数技术、小的计数器、看门人技术和reset机制来减少了元数据开销并保证了数据的鲜活性,但是在缓存样本较小时会有一些除2的截断问题。6.有突发流量进入时,属于新爆发产生的条目在被驱逐之前没有建立足够的频率来保持在缓存中,这导致了重复的缓存穿透,这个场景下TinyLFU就会存在一些问题。7.通过设计一个名为Window TinyLFU (W-TinyLFU)的策略,在我们的Caffeine集成中解决了这个问题,该策略包含两个缓存区域。主缓存使用SLRU驱逐策略和TinyLFU允许策略,而窗口缓存使用LRU驱逐策略,而不使用任何允许策略。SLRU策略在主缓存中的A1和A2区域被静态划分,因此80%的空间被分配给热项(A2),被驱逐者则从20%的非热项(A1)中选取。任何到达的项总是允许进入窗口缓存,而窗口缓存的被驱逐者也有机会进入主缓存。如果它被承认,那么W-TinyLFU的被驱逐者就是主缓存的被驱逐者,否则就是窗口缓存的被驱逐者。8.在当前的Caffeine(2.0)版本中,窗口缓存的大小是总缓存大小的1%,主缓存的大小是99%。W-TinyLFU背后的动机是让该方案在处理LFU工作负载时表现得像TinyLFU一样,同时仍然能够利用LRU模式(比如突发)。因为99%的缓存分配给主缓存(使用TinyLFU),所以对LFU工作负载的性能影响可以忽略不计。另一方面,一些工作负载允许利用LRU友好的模式。在这些工作中W-TinyLFU比TinyLFU更好,但是在有些场景中W-TinyLFU占用内存可能会更高。9.CountMin Sketch[1]:它使用一个计数器矩阵和多个哈希函数。添加一个条目会使每一行增加一个计数器,并且通过取观察到的最小值来估计频率。这种方法通过调整矩阵的宽度和深度,让我们在空间、效率和碰撞导致的错误率之间进行权衡。
10.W-TinyLFU使用Sketch作为过滤器,如果它有一个新的入口比入口更高的频率将不得不被驱逐为它腾出空间。不是立即过滤,一个准入窗口给一个入口机会来建立它的流行。这避免了连续的遗漏,特别是在稀疏爆发的情况下,其中一个条目可能被认为不适合长期保留。为了保持历史记录的新鲜,将定期或增量地执行老化过程,以将所有计数器减半。
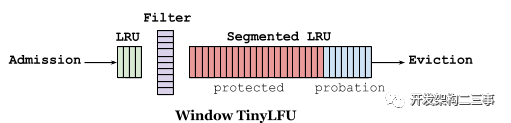
W-TinyLFU使用分段LRU (SLRU)策略进行长期保留。一个条目从预备段开始,在随后的访问中,它被提升到受保护的段(容量上限为80%)。当受保护的段已满时,它将被驱逐到预备段,这可能会触发一个被丢弃的预备段。这确保了具有较小重用间隔的条目(最热门的)被保留,而那些不太经常重用的条目(最冷的)将有资格被逐出。
1. 介绍
缓存是计算机科学中提高系统性能的最基本、最有效的方法之一。它是通过将一小部分数据项保存在更快和/或更接近应用程序的内存中来获得的,这些内存的设置使得整个数据域无法装入这个快速附近的内存中。缓存能够工作的直观原因是,在计算机科学的许多领域中,数据访问显示出相当程度的局部性。捕捉本地更正式的方法是描述所有可能的数据项的访问频率通过一个概率分布,并指出在许多有趣的计算机科学领域,概率分布是高度倾斜,这意味着少量的对象更可能比其他对象访问。此外,在许多工作负载中,访问模式以及相应的概率分布会随时间变化。这种现象也被称为时间局部性。
当一个数据项被访问时,如果它已经出现在缓存中,我们说有一个缓存命中;缓存命中的次数和数据访问的总次数之间的比率被称为缓存命中比率。因此,如果保存在缓存中的项对应于访问最频繁的项,那么缓存很可能产生较高的命中率。
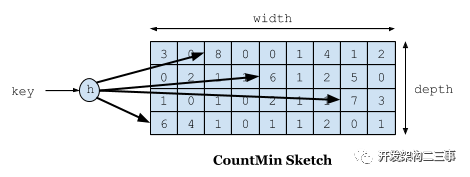
由于缓存大小通常是有限的,缓存设计者面临着如何选择存储在缓存中的项的困境。特别是,当为缓存保留的内存满时,决定应该从缓存中驱逐哪些项。显然,驱逐决策应该以有效的方式进行,以避免出现回答这些问题所需的计算和空间开销超过使用缓存所带来的好处的情况。缓存机制用来决定哪些项和哪些项应该插入缓存的空间。
当数据访问模式的概率分布随时间不变时,很容易看出使用频率最低(LFU)的缓存命中率最高。根据LFU,在一个大小为n个条目的缓存中,在每个时刻,到目前为止的n个最经常使用的条目被保存在缓存中。然而,LFU有两个明显的局限性。首先,已知的LFU实现需要维护大而复杂的元数据。其次,在大多数实际工作负载中,访问频率会随着时间发生根本变化。例如,考虑一个视频缓存服务,某天非常流行的视频片段可能几天后就不会被访问了。因此,一旦该项的流行度消退,仅仅因为它曾经非常流行就将其保留在缓存中是没有意义的。
让我们注意到,由于为所有遇到的对象维护频率直方图的成本太高,已经发布的实现LFU方案的作品只维护当前存在于缓存中条目的频率直方图的写、读和时间。因此,我们通过将前者(维护全量的缓存访问频率)称为完美的LFU (PLFU)而将后者(只维护当前在内存中的缓存的读写频率)称为内存中的LFU来区分它们。由于WLFU优于内存中的LFU8[2],这里我们只处理WLFU和PLFU。
LFU的一个流行的替代方法依赖于时间局部性属性,这个替代方法称为“最近最少使用”(LRU),通过它,最后访问的项总是插入到缓存中,而最近最少访问的项则被驱逐(当缓存已满时)。与LFU相比,LRU的实现效率更高,可以自动适应数据访问模式的时间变化和工作负载的激增。然而,在许多工作负载下,为了获得相同的命中率,LRU需要比LFU大得多的缓存(因为无法保证缓存的命中率,低命中率的缓存也会在内存中存放较长时间)。同时对于硬件缓存和操作系统页面缓存来说,LRU仍然被认为太慢,因此在这些高要求的情况下,我们发现使用LRU的近似实现比精确的LRU实现效果更好。
贡献
本文的主要贡献是展示了利用近似LFU的允许策略扩充缓存的可行性和有效性。
这包括以下几个方面:
首先,我们提出一个缓存结构,在这种结构中,一个访问项目只是插入到缓存如果承认政策决定,缓存命中率可能会受益于取而代之的缓存受害者(选择的缓存替换策略)。其次,我们开发了一种新的高空间效率的数据结构,昵称TinyLFU,它可以代表非常大的访问样本的可适应的近似LFU统计量。例如,实现TinyLFU所需的元数据(即使涉及数百万项的域)可以放在一个内存页面中,因此可以固定在物理内存中,从而实现快速操作。我们通过正式的分析和模拟表明,尽管是近似的,TinyLFU获得的频率排序与这些项目的真实访问频率直方图中出现的相应排序非常相似。
第三,我们报告了将TinyLFU集成到Caffeine高性能Java缓存开源项目[43]中的情况。特别地,这一部分包括TinyLFU的另一个优化,称为W-TinyLFU,以更好地处理突发的工作负载。
第四,我们对TinyLFU增强的回收策略进行了广泛的性能研究,并将它们与其他多个缓存管理策略进行比较,包括最先进的策略,如LIRS[36]和ARC[44,45]。我们展示了对于倾斜的工作负载,无论是合成的还是真实世界的轨迹,TinyLFU允许策略显著提高了几种已知的驱逐策略的性能。事实上,在静态分布中,应用TinyLFU录取策略后,各种驱逐策略之间的差异变得非常小。也就是说,即使是最幼稚的驱逐策略也会产生与真正的LFU几乎相同的性能。在实际(动态)分布的情况下,智能的收回策略仍然有影响,但影响要比没有允许策略(允许缓存驻留的策略)的情况小得多。此外,在我们测试的各种轨迹中,W-TinyLFU 的命中率超过或等于我们试验过的所有其他缓存管理策略,而且它是唯一执行得如此一致的策略。实际上,对于大多数轨迹,甚至使用TinyLFU允许策略增强的LRU驱逐策略也可以获得相同的(最好的)结果。
本文的其余部分组织如下:相关工作将在第2节中讨论。我们在第3节介绍TinyLFU。第4节描述了TinyLFU在Caffeine中的使用和我们的新W-TinyLFU。性能测试报告在第5节中,最后我们将在第6节中进行讨论。
2. 相关工作
2.1 缓存更迭
如引言所述,虽然PLFU是在访问分布为静态时的最优策略,但对所有曾访问的数据项保持完整的频率直方图的代价高得令人难以接受,而且PLFU不适应分布中的动态变化。因此,提出了几种备选办法。
内存LFU只维护缓存中已经存在的数据项的访问频率,并且总是将最近访问的数据项插入到缓存中,如果需要,将删除缓存[48]中访问频率最低的数据项。内存中的LFU通常使用堆来维护。管理LFU堆的时间复杂度一直被认为是O(log(N)),直到最近,在[40]中显示了一个O(1)构造。然而,即使有了这样的改进,内存中的LFU对频率分布变化的反应仍然很慢,并且它的性能与静态分布的PLFU相比有很大的延迟,因为它没有为不再在缓存[48]中的项保持任何频率统计。
在[3]中引入老化以提高内存LFU对变化的反应能力。它是通过限制缓存项的最大频率计数以及偶尔将缓存项的频率计数除以一个给定的因子来获得的。决定何时除以计数器和除以多少是很棘手的,需要对[2]进行微调。
如上所述,WLFU只维护最后一个W请求[38]的窗口的访问频率。为了维护这个窗口,该机制需要轨迹请求的顺序,这增加了开销。然而,WLFU比PLFU更能适应接入分布的动态变化。
ARC[44,45]通过维护两个LRU列表中的元数据,结合了近效性和频率。第一个反映的是仅被访问过一次的项,而第二个则对应于在最近历史中至少被访问过两次的项。ARC根据两个列表的命中率来平衡缓存内容源,从而调整自己以适应工作负载的特性。为此,ARC监视最近从缓存中清除的项的访问数据。如果再次命中从LRU列表中删除的项,ARC将扩展这个列表,并表现得更像LRU。如果命中了最近从第二个LFU列表中被逐出的项,ARC将扩展LFU列表的大小,其行为更类似于LFU。监视最近从缓存中清除的项的技术称为ghost条目,这种技术在最新的缓存策略中非常常见。
LIRS[36](Low Inter-reference Recency Set)是一种页面替换算法,它尝试使用名为重用距离的度量标准直接预测某个项的下一次出现。为此,LIRS监视缓存中许多过去项和从缓存中驱逐的项前到达时间。因此,LIRS还维护大量的ghost条目。
分段LRU (SLRU)[39]策略通过区分在短时间内至少访问两次的暂时流行项与在此期间只访问一次的项来捕获最近流行的情况。这一区别是通过两个固定大小的LRU段来管理缓存的,一个试用段(A1)和一个受保护段(A2)。新项目总是插入到试用部分。当一个已经在试用段中的项目再次被访问时,它被移动到受保护的段中。如果试用段已经满了,根据LRU政策,对它的插入会导致驱逐(和遗忘)其中的一个条目。类似地,对完全受保护段的任何插入都会导致驱逐其LRU中最早被访问的元素。然而,在这种情况下,最早被访问的元素被重新插入试用部分,而不是完全被遗忘。这样,到达受保护段的暂时流行项将比不流行项在缓存中停留的时间更长。
2Q[37]是一个用于操作系统的页面替换策略,它管理两个FIFO队列A1和A2。A1被分成两个子队列,A1in(常驻)和A1out(非常驻)。当第一次访问一个项时,它会被输入到A1in中,直到在FIFO策略下被逐出。但是,当从A1in或A2中驱逐一个项时,它被插入到A1out中。如果一个被访问的项既不在A1in中,也不在A2中,但是它出现在A1out中,那么它将被插入A2中。
LRU- k[47]还结合了LRU和LFU的理念。在这个策略中,每个元素的最后K次出现都被记住。通过使用这些数据,LRU-K从统计上估计项目的瞬时频率,以便将最频繁的页面保存在内存中。
Web缓存方案通常还会考虑对象的大小。例如,SIZE[56]提供简单地首先删除最大的项,而相同大小的项由LRU订购。当选择一个缓存驱除项时,LRU-SP[11]衡量一个条目的大小和频率。
GDSF[13]是一种混合的Web缓存策略,它在决策中结合了最近一次访问的频率、将对象带到缓存的成本、对象大小和频率。它是对贪婪对偶算法[57]的改进,只考虑大小和代价。在[4]中,当数据是分层的时,工作负载也会考虑延迟,也就是说,为了获取子项,必须首先获取它的前一项。
[53]中引入了一种与我们的方法相关的方法,它建议使用热列表来增强已知的缓存算法。这个列表显示了使用某种衰变机制的最流行的项目。热列表中的项优先于回收策略中的其他项。但是,是否退出缓存中的项的决定并不取决于该项与当前访问的项的相对频率。此外,必须维护一个包含n个项的显式列表。[53]中展示了这种方法,在一定程度上提高了各种缓存建议的命中率,但代价是大量的元数据开销。
总之,TinyLFU与上述建议相关联,它是一种可以用于增强其他缓存策略的机制,通过对大型历史数据进行近似统计来增强它们,同时提供快速访问时间和较低的元数据开销。
2.2 近似地计数体系
近似计数技术广泛应用于许多网络应用中。最初开发近似计数是为了维护每个流的网络统计数据。这些结构对于缓存也很有吸引力,因为它们提供了非常快的更新并且占用了紧凑的空间。
抽样方法[16,35,25]提供了较小的内存占用,但需要显式地表示所有的键。而且,它们通常会遇到较大的误差范围。因此,我们选择不使用它们,因为在我们的环境中,键的大小是总体成本的重要组成部分。其他方法,如计数器编织[42]减少元数据大小,但需要一个长解码操作,因此不适用于高速缓存。另一种方法是压缩计数器表示本身[52,34,54,20]。在TinyLFU中,我们设法用短计数器表示直方图,因此这些方法对我们没有帮助。
多哈希草图,如Spectral Bloom Filters(SBF)[17]和计数最小草图(CMSketch)[18]在我们的上下文中很有吸引力。由于这些草图隐式地关联键和计数器,因此不需要在频率直方图中存储键。然而,它们对我们的情况不是最佳的。特别地,SBF包括一个旨在实现可变大小计数器的复杂实现。在我们的示例中不需要如此复杂的实现,因为我们只需要很小的计数器。另一方面,CM-Sketch提供了一个简单的实现,但相对不准确,因此比计数Bloom Filter占用更多的空间[27]。
当所有增量都为正时,最小增量方案也被称为保守更新,它被用来提高Counting Bloom Filters的准确性[17,26,23]。该技术已成功应用于多个领域[46,50,5,32,7,6,41,31,30]。
2.3 有趣的缓存应用
数据缓存可以用作云服务[14,15]。MemcacheD[28]允许在内存中缓存数据库查询和与之相关的条目,它被许多现实生活中的服务广泛部署,包括Facebook和Wikipedia。
缓存也被用于路由器内部的数据中心的网络级别,使用一种称为网络内缓存的技术[49,10]。该技术允许显式地命名内容,并允许数据中心中的路由器缓存数据以增加网络容量。在对等系统中,TinyLFU还被用于加速Kademlia查找过程[24],有效地增加容量并减少延迟。
TinyLFU可以集成在上面所有的例子中。对于网络内缓存,TinyLFU非常有吸引力,因为它需要非常小的内存开销,并且可以在硬件上高效地实现。对于MemcacheD和云缓存服务,[28,15]的eviction策略是LRU的一种变体,不存在允许策略。如本文所示,在LRU驱逐策略中加入一个基于TinyLFU的允许策略可以大大提高其性能。
3. TinyLFU 架构
3.1 TinyLFU概览
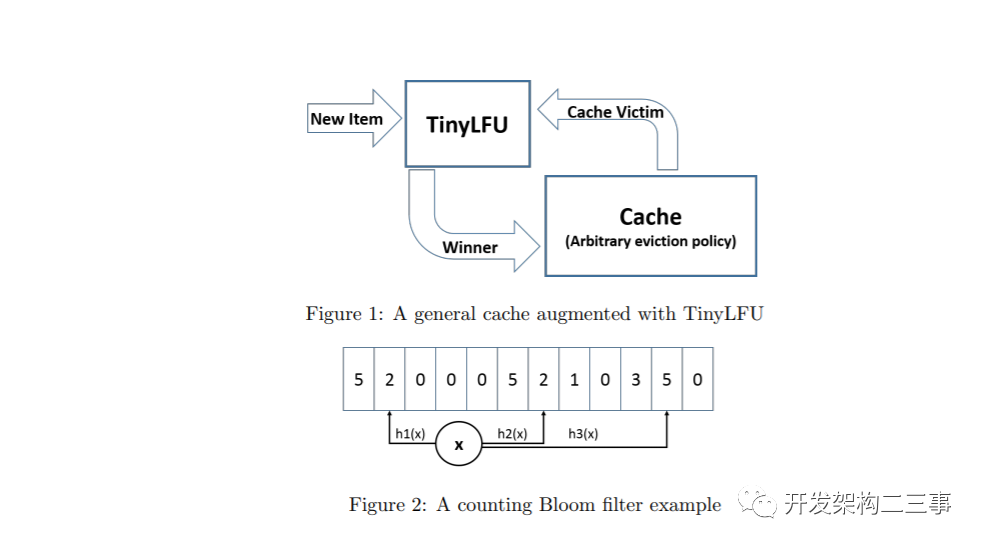
TinyLFU的架构如图1所示。在这里,缓存清除策略选择一个缓存驱逐对象,而TinyLFU决定是否用新项替换缓存驱逐对象以增加命中率。
为此,TinyLFU维护了一个相当大的近期历史上项目频率的统计数据。对于实际实现来说,存储这些统计数据被认为是非常昂贵的,因此TinyLFU以一种高效的方式逼近它们。在下面,我们将描述TinyLFU所使用的技术,其中一些是对已知的粗略计算技术的修改,而另一些则是特别为缓存上下文而创建的新思想。
让我们强调,我们面临两大挑战。第一个是保持一个新鲜机制,以保持最近的历史和删除旧的事件。其次是内存消耗开销,为了将其视为一种实用的缓存管理技术,应该对其进行显著改进。
3.2 近似计算概述
计数式布隆过滤器是一个其中矢量中的每一项都是一个计数器,而不是一个位的布隆过滤器。因此,这些条目在插入/添加操作中递增,而不是在对应于过滤器散列函数的索引处设置位。
最小增量CBF是一个增强计数布隆过滤器,它支持两种方法:添加和估计。估计方法是通过计算键的k个不同哈希值来执行的。每个散列值都被视为一个索引,并读取该索引处的计数器。这些计数器的最小值是返回值。Add方法还为键计算k个不同的散列值。但是,它读取所有k个计数器,只增加最小的计数器。例如,假设我们使用3个哈希函数,如图2所示。物品到达后,3个计数器被读取。假设我们读取了{2,2,5},Add操作只将剩下的两个计数器从2增加到3,而第三个计数器保持不变。直观地说,这个添加操作可以防止对大型计数器进行不必要的增量,并对高频项产生更好的估计,因为它们的计数器不太可能由大多数低频项进行增量。它不支持衰减,但经验表明,减少误差的高频计数[17]。
其他近似计数方案:如上所述,CM-Sketch是另一种流行的近似计数方案[18]。它提供了一个较低的精度每空间折衷。然而,人们普遍认为它的速度更快。下面我们描述的空间优化和老化机制也同样适用于CM-Sketch。下面对TinyLFU的描述忽略了计数布隆过滤器和CM-Sketch之间的选择。
3.3 保持新鲜的机制
据我们所知,仅在[19]中研究了保持近似草图新鲜的问题,其中滑动样本是通过保持m个不同草图的有序列表来获得的。新项目被插入到第一个草图中,在固定数量的插入之后,最后一个草图被清除并移动到列表的头部。这样,过去的事情就被遗忘了。
作为频率直方图,[19]方法不是很有吸引力,原因有二:首先,为了评估一个项目的频率,要读取m个不同的近似草图,导致许多内存访问和哈希计算。其次,这种方法增加了空间消耗,因为我们需要在m个不同的草图中存储相同的项目,并且每个项目被分配了更多的计数器。
相反,我们提出了一种新的方法来保持草图的新鲜度,重置(reset)方法如下所述。重置操作很简单,每当我们向近似图中添加一项时,我们就增加一个计数器。一旦这个计数器达到样本大小(W),我们将它和5近似图中的所有其他计数器除以2。这种划分有两个有趣的优点。首先,它不需要太多的额外空间,因为它增加的内存成本只是一个Log(W)位的计数器。其次,正如我们在分析和实验中所展示的,这种方法提高了高频项目的准确性。由于近似值草图的精度总是可以通过使用更多的空间来提高,我们证明,重置方法实际上降低了总空间成本,因为我们在相同的空间中得到了更精确的草图。
这个操作的缺点是一个昂贵的不频繁的操作,它会遍历近似方案中的所有计数器,然后将它们除以2。然而,用2除法可以有效地在硬件上使用移位寄存器实现。同样,在软件中,移位和掩码操作允许同时对多个(小)计数器执行此操作。最后,它的平摊复杂度是常数,这使得它在许多应用中都是可行的。
由于我们使用了整数除法,因此显示为3的计数器将被重置为1而不是1.5,从而导致截断错误。在下面的小节中,我们证明了复位操作的正确性,并评估了复位操作的截断误差。
3.3.1 重置正确性
在本节中,我们将分析TinyLFU操作,前提是计数基础设施能够准确工作。在结果部分中,我们将探讨需要多少空间来保持与精确计数技术相同的性能。

3.3.2 重置截断误差
由于我们的重置操作使用整数除法,它引入了截断错误。也就是说,在复位操作之后,计数器的值可能比浮点计数器的值低0.5。如果我们必须再次复位,在复位之后,前一个复位操作的截断误差除以0.25,但是我们积累了一个新的截断误差0.5,导致总误差为0.75。很容易看出,最坏情况下截断误差最多收敛到比项的准确率低一点。因此,截断错误对一个项目的记录发生率的影响在复位操作后高达2/w。这意味着样本容量越大,截断误差越小。
3.4 空间简化
我们的空间缩减是在两个独立的维度上获得的:首先,我们减少了近似草图中每个计数器的大小。其次,我们减少了由草图分配的计数器的总数。下面详细介绍了这些节省空间的优化。
3.4.1 很多小的计数器
简单地实现一个近似草图需要使用长计数器。如果一个草图包含W个唯一的请求,它就需要允许计数器计数直到W(因为在这样一个样本中,一个项原则上可以被访问W次),从而导致每个计数器的日志(W)位,这可能会非常昂贵。幸运的是,复位操作和下面的观察结果的结合大大减少了计数器的大小。
具体地说,频率直方图只需要知道缓存中已经存在的潜在缓存驱逐对象是否比当前被访问的项更受欢迎。然而,频率直方图不需要确定缓存中所有项之间的确切顺序。此外,对于大小为C的缓存,所有访问频率在1/C以上的条目都属于缓存(合理假设被访问的条目总数大于C),因此,对于给定的样本大小W,我们可以安全地将计数器设置为W/C。
请注意,这种优化是可能的,因为我们的老化机制是基于重置操作而不是滑动窗口的。滑动窗口,在一个访问模式之间的一些项目我交替W / C连续访问之后,W / C + 1访问其他项目,这可能发生,我将尽快驱逐滑动窗口的变化超出了至少最近W / C访问第i个条目即使第i个条目是最经常访问的缓存项。
为了感受一下计数器的大小,当W/C = 8时,每个计数器只需要3位,因为样本比缓存本身大8倍。为了比较,如果我们考虑一个样本大小为16K的2K个小缓存,并且我们不使用小计数器优化,那么所需的计数器大小为14位。
3.4.2 Doorkeeper(看门人机制)
在许多工作负载中,特别是在重尾部工作负载中,不受欢迎的项占所有访问的很大一部分。这一现象意味着,如果我们计算样本中每个唯一项出现的次数,那么大多数计数器将分配给那些在样本中不太可能出现多次的项。因此,为了进一步减小计数器的大小,我们开发了Doorkeeper机制,使我们能够避免向大多数尾部对象分配占多个bit的计数器。
看门人是一个放置在近似计数方案前面的规则布隆过滤器。物品到达后,我们首先检查该物品是否包含在门卫中。如果它不包含在门卫中(正如第一次计时器和尾项所期望的那样),则将该项目插入到门卫中,否则将插入到主结构中。在查询项目时,我们同时使用门卫和主结构。也就是说,如果该物品包含在Doorkeeper中,TinyLFU估计该物品的频率为其在主结构中的估计值加上1。否则,TinyLFU只返回来自主结构的估算值。
当执行复位操作时,除了将主结构中的所有计数器减半之外,我们还清除了看门人。这样做使我们能够删除所有关于第一次计时器的信息。需要注意的是,清理门卫也把对每一项的估计值降低了1,这也将截断误差增加了1。
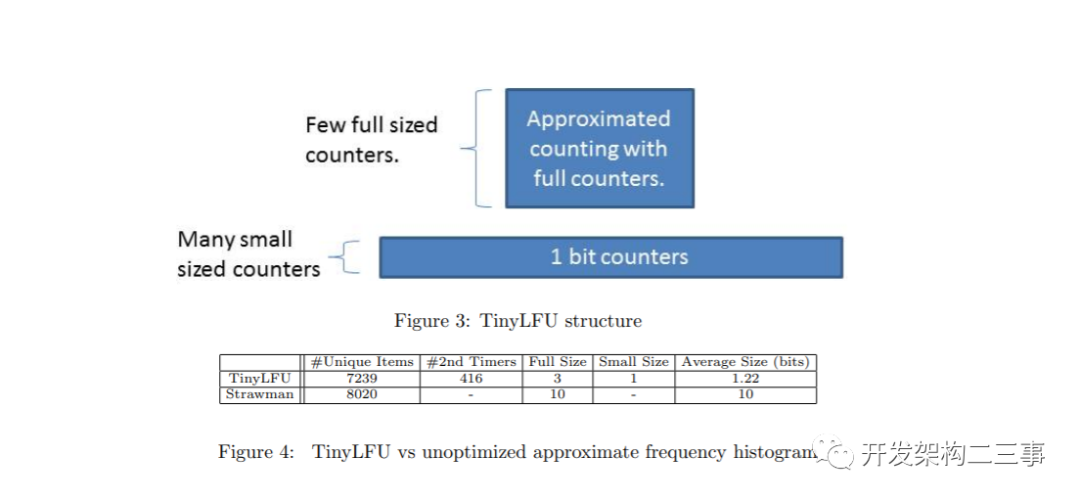
内存方面,尽管门卫需要额外的空间,但它允许主结构更小,因为它限制了插入到主结构的独特物品的数量。特别是,大多数尾项只分配1位计数器(在Doorkeeper中)。因此,在许多倾斜的工作负载中,这种优化显著减少了TinyLFU的内存消耗。TinyLFU和看门人如图3所示。我们注意到,类似的技术在网络安全的上下文中曾被提出过[9]。
3.5 测试用例:TinyLFU VS Strawman
为了证明TinyLFU的设计,我们将其与strawman进行比较。strawman相当于仅使用现有的近似计数建议构建频率直方图。为了使strawman保持新鲜,它使用了[19]中提出的滑动窗口近似。也就是说,strawman使用10种不同的近似计数草图来模拟滑动窗口。此外,strawman的计数器上没有看门人或上限,因此需要允许其计数器增长到最大的窗口大小。
我们的测试用例是一个1K项的缓存,增加了9K项的频率直方图。对于这个工作负载,TinyLFU要求它的计数器数到9。除了可以数到1的看门人之外,还可以使用可数到8的3位满计数器来获得此计数。strawman使用10个大约的计数草图,每个草图包含900个项目,它的计数器大小为10位。在本例中,我们考虑的是Zipf 0.9发行版,它是许多有趣的现实工作负载的特征,例如[8,51,29]。
我们在图4(见上图)中总结了这两个频率直方图的存储需求。可以看到,在这个工作负载中,TinyLFU需要存储的惟一值减少了大约10%,因为它使用的是一个大草图,而不是10个小草图。此外,在这个实验中,绝大多数物品只消耗了一个1位的小计数器。由于小计数器的优化,在这个示例中出现多次的频繁项被分配了一个额外的3位计数器。总的来说,对于这个工作负载,我们注意到TinyLFU将strawman的内存消耗减少了89。
3.6 连接TinyLFU到缓存
将TinyLFU连接到LRU和随机缓存,同时将缓存视为黑盒,这很简单。然而,由于TinyLFU使用了一种重置方法,使得条目的频率减半,我们不得不修改LFU缓存的实现,以便与TinyLFU正确地连接。特别是,我们必须同步TinyLFU的重置操作和缓存,并重置缓存项的频率。
4. W-TinyLFU的优化
TinyLFU被集成到开源的Java高性能缓存库[43]Caffeine中。在对这个库进行广泛的基准测试时,我们发现,尽管TinyLFU在源自Internet服务的轨迹和人工类似zipf的轨迹上表现良好,但在一些工作负载中,与先进的缓存策略相比,TinyLFU的表现并不好。这种情况主要发生在轨迹中,包括对同一对象的稀疏爆发(突然产生的流量,但积累的次数不够),这在存储服务器中很常见。也就是说,在这些情况下,属于新爆发产生的条目在被驱逐之前没有建立足够的频率来保持在缓存中,这导致了重复的缓存穿透。
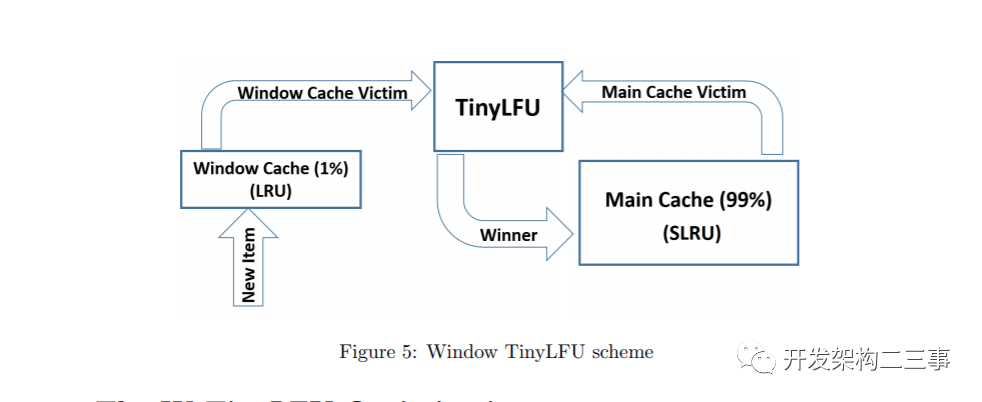
通过设计一个名为Window TinyLFU (W-TinyLFU)的策略,在我们的Caffeine集成中解决了这个问题,该策略包含两个缓存区域。主缓存使用SLRU驱逐策略和TinyLFU允许策略,而窗口缓存使用LRU驱逐策略,而不使用任何允许策略。SLRU策略在主缓存中的A1和A2区域被静态划分,因此80%的空间被分配给热项(A2),被驱逐者则从20%的非热项(A1)中选取。
任何到达的项总是允许进入窗口缓存,而窗口缓存的被驱逐者也有机会进入主缓存。如果它被承认,那么W-TinyLFU的被驱逐者就是主缓存的被驱逐者,否则就是窗口缓存的被驱逐者。W-TinyLFU方案如图5所示(见上图)。
在当前的Caffeine(2.0)版本中,窗口缓存的大小是总缓存大小的1%,主缓存的大小是99%。W-TinyLFU背后的动机是让该方案在处理LFU工作负载时表现得像TinyLFU一样,同时仍然能够利用LRU模式(比如突发)。因为99%的缓存分配给主缓存(使用TinyLFU),所以对LFU工作负载的性能影响可以忽略不计。另一方面,一些工作负载允许利用LRU友好的模式。在这些工作中W-TinyLFU比TinyLFU更好。正如我们在下面的第5部分所报告的,对于Caffeine的需求,W-TinyLFU是一种更广泛的工作量的首选选择,因此增加的复杂性是合理的。
TinyLFU作为一个迟到者被加入到Caffeine项目中。我们在这方面的经验表明,与其他最先进的方案相比,TinyLFU在质量上有一些好处。正如我们上面提到的,后者通常维护ghost条目,这增加了实现的复杂性。而且,它们会带来更高的内存开销。Caffeine中的W-TinyLFU的总体空间开销为每个缓存条目8字节,这明显低于ARC和LIRS的开销。另外,在TinyLFU(和W-TinyLFU)的情况下,开发时间要快得多,因为该策略的侵入性较低,因为不需要重新设计主要驱逐方案来考虑ghost条目对其他数据结构的污染。
5. 实验结果
5.1 方法论
在本节中,我们将研究TinyLFU作为一种实用的缓存允许策略的效用。我们的评估分为三个部分:首先,在5.2节中,我们研究了使用TinyLFU接纳策略增加三个基线驱逐策略(即LRU、Random和LFU)的影响。这一部分是使用Java原型执行的,该Java原型可以用给定的缓存大小(根据它可以存储的项的数量)实例化,一个包含访问轨迹的文件,以及上述缓存管理方案之一。然后,原型使用该文件,根据所选择的管理方案和缓存大小以及总体统计数据,返回每次访问的结果。原型使用计数布隆过滤器和所有优化描述在第1节。
我们在5.3节中报告的第二组评估使用实际的Caffeine实现[43]执行。在Caffeine的当前版本(2.0)中,TinyLFU直方图被维护为10倍于缓存大小的样本。此外,Caffeine使用CM-Sketch(与我们的空间优化和老化机制)而不是计数布隆过滤器,因为即使CM-Sketch如此大的样本,每个缓存项目只需要8字节,另一方面Caffeine的任务是高吞吐量(总的元数据大小会更大,因为LRU策略是作为一个队列来维护的,它带有向前和向后指针,为内存中的每个项添加两个指针)。我们比较了获得的大量缓存管理策略的命中率。然而,为了简洁起见,我们只报告表现最好的那些。在测量的第三组,在第5.4节我们探索由TinyLFU的各种机制积累的各种类型的误差以及总误差。
为了进行评估,我们使用了Zipf 0.7和Zipf 0.9(我们对其他几个偏态分布进行了实验,得到了非常相似的定性结果。)的常数分布和类似spc1的合成轨迹44[3]以及真实轨迹。在合成的Zipf轨迹中,按照对应的分布从100万个对象中选取项目。此外,缓存的预热时间很长(是样本大小的20倍),我们以最高的命中率呈现它们。类似spc1的轨迹除了随机访问之外还包含长顺序扫描,并且页面大小为4千字节[44]。在真实的轨迹中,缓存没有预热;由于分布是随时间逐渐变化的,所以不需要预热。
我们实际的工作负载来自各种来源,并表示多种类型的应用程序,如详细说明的那样
下图:
•YouTube: YouTube轨迹是从YouTube数据集[12]生成的。特别是[12]中的轨迹包括每周对每个视频访问次数的总结,而不是连续的请求时间线。因此,对于每个报告的周,我们都计算了相应的近似访问分布,并生成了每周遵循该分布的合成访问。•维基百科:包含2007年9月开始[55]两个月内10%的维基百科流量的维基百科追踪。•DS1:取自[44]的数据库轨迹。•S3:从[44]获取的搜索引擎轨迹。•OLTP: 对OLTP服务器[44]的文件系统的轨迹。需要注意的是,在典型的OLTP服务器中,大多数操作是在内存中的对象上执行的,因此不会直接反映磁盘访问。因此,大多数磁盘访问都是写入事务日志的结果。也就是说,轨迹主要包括顺序块访问的升序列表,由于偶尔的写重放或内存缓存丢失,零星存在一些随机访问。•P8和P12:两个windows服务器轨迹[44]。•Glimpse:Glimpse系统的一个轨迹,描述分析查询[36]的执行。此轨迹的主要特征是下划线循环以及其他类型的访问。•F1和F2: 来自两个大型金融机构运行的应用程序的轨迹,取自Umass轨迹存储库[1]。出于上面提到的相同原因,它们在结构上与OLTP轨迹非常相似。•WS1, WS2, and WS3: 另外三个搜索引擎轨迹,也取自UMass存储库[1]。
注意,DS1、OLTP、P8、P12和S3轨迹是由ARC[44]的作者提供的,它们代表了潜在的ARC应用。ARC[44]的作者也发现了类似spc1的合成痕迹。类似地,Glimpse轨迹由LIRS[36]的作者提供。
我们还使用了YouTube的工作负载来衡量动态分布对性能的影响。为了做到这一点,我们没有在一周内播放全部的视图,而是每周只播放一些样本。这些测试模拟工作负载非常动态时缓存的行为。
在我们的图中,LRU和Random指的是驱逐策略,而TLRU和TRandom分别指的是由TinyLFU增强的LRU和随机缓存。对于LFU缓存回收,我们测试了两个选项:同时使用LFU回收策略的WLFU和使用精确滑动窗口实现的LFU许可策略。TLFU是我们用TinyLFU扩展的LFU缓存的名字。此外,ARC代表ARC,LIRS代表LIRS,而W-TinyLFU代表W-TinyLFU方案(1%LRU窗口缓存,99%主缓存由TinyLFU允许策略和SLRU清除策略管理)。在我们研究W-TinyLFU不同窗口缓存大小的图中,窗口大小写在括号中,例如,W-TinyLFU(20%)表示一个窗口缓存消耗了总缓存大小的20%。
5.2 TinyLFU增强缓存的结果
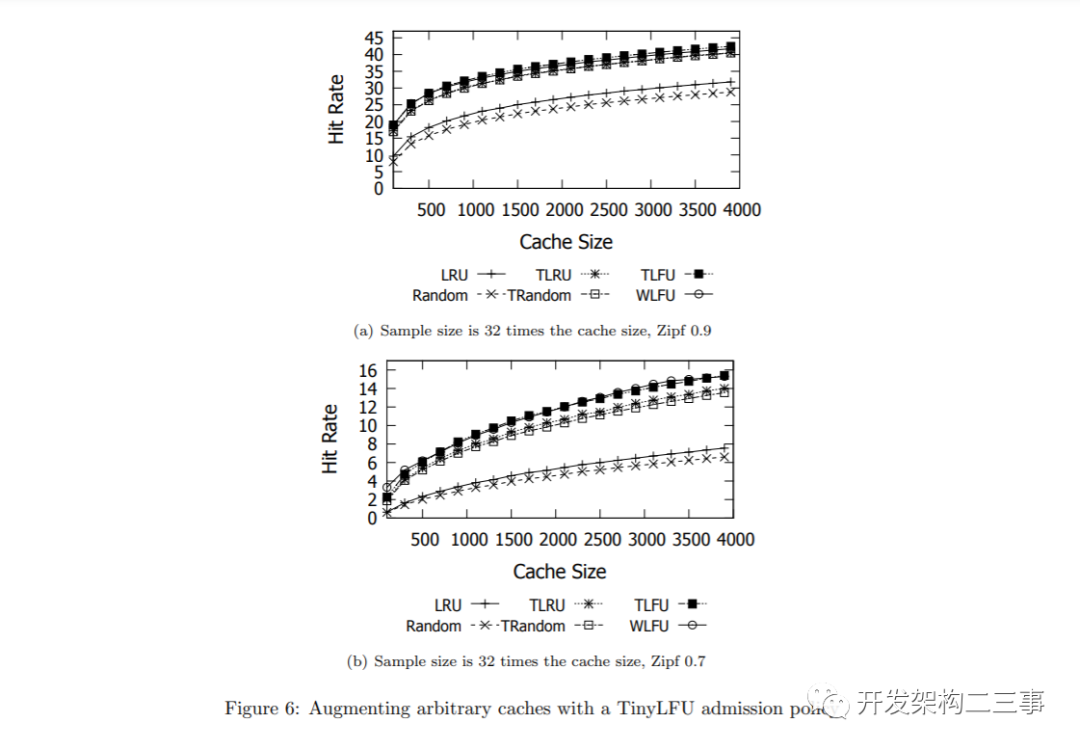
图6显示了TinyLFU录取策略在常量偏态分布下对上述几种驱逐策略性能的影响。可以看到,在常量分布下,所有使用TinyLFU增强的缓存都以类似的方式运行。令人惊讶的是,与TinyLFU增强LRU和随机技术相比,LFU缓存清除只产生了边际效益。让我们注意到,在这种倾斜分布中,无论缓存的大小如何,理论上最大缓存命中率都是有界的。直观地看,对于一个分布函数fi,这个界可以通过对max(0, fi -1)的积分(因为第一次出现总是错过)除以对fi的积分粗略地计算出来。
我们得出结论,对于常偏态分布,TinyLFU缓存允许策略是一个有吸引力的增强。虽然增加内存中的LFU会产生略高的命中率,但内存中的LFU的开销可能需要使用更简单的缓存回收策略。特别地,LRU和Random在命中率相当时需要的开销较低。
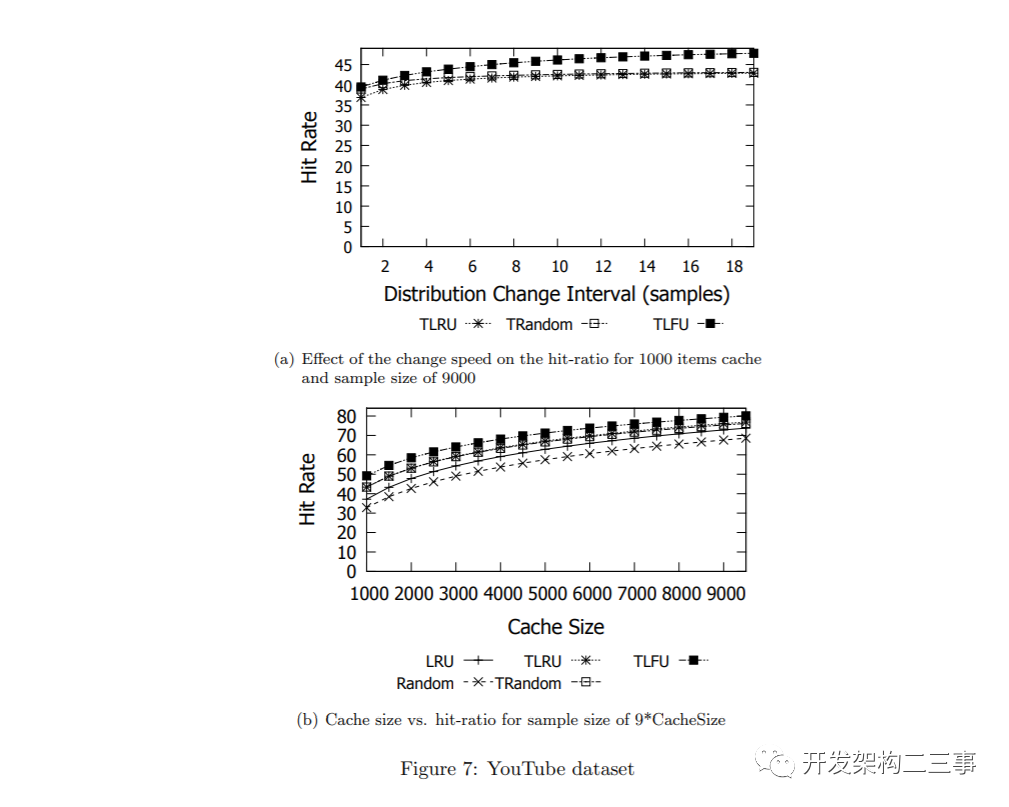
我们做的第二个实验是在一个动态发行版上测试增强的缓存。为此,我们使用了一个数据集来描述从2008年4月16日开始的21周内161K个新创建的YouTube视频的流行程度。我们评估了每个视频每周的近似频率,并创建了一个代表每周的分布。因此,我们的实验在每个给定数量的请求之间交换这些分布。
我们测量了两个指标:第一个是我们能以多快的速度改变分布,也就是说,我们从每周分布中执行的样本数量对TinyLFU增强缓存的命中率有什么影响。第二,当从轨迹中取分布变化速度时,缓存大小对所实现的命中率的影响。
实验结果如图7所示。可以看到,即使在动态工作负载中,TinyLFU在增加任意缓存方面也是有效的。此外,正如所有LFU缓存所期望的那样,当分布变化更慢时,好处更大。然而,在这个工作负载中,增加的随机缓存和增加的LRU缓存与真正的LFU缓存之间的差别更大。因此,在动态工作负载中选择正确的缓存被驱逐者似乎比在静态工作负载中更重要。
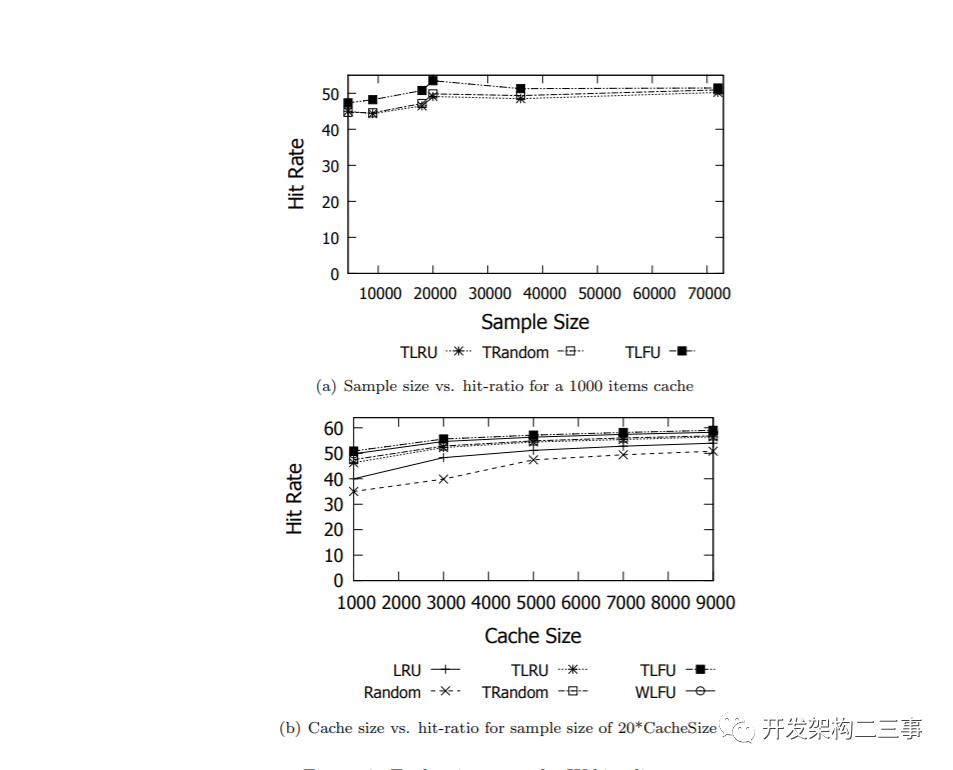
我们做的第三个测量是在维基百科访问追踪上进行的实验。首先,我们研究了样本大小和缓存大小之间的必要比例,样本为来自轨迹中不同点的1亿个连续请求。其次,我们使用找到的最佳比率,并在不同的缓存大小上测试它。这些结果如图8所示。与静态工作负载不同,现实生活中的工作负载会随着时间逐渐变化。因此,使用非常大的样本甚至可以降低获得的命中率,因为它降低了缓存适应工作负载的速度。
我们注意到,尽管WLFU和TLFU实现了几乎相同的命中率,但WLFU和TLFU之间的主要区别在于它们的元数据成本。例如,在YouTube工作负载中,每个样例元素只使用0.57字节。因为TinyLFU统计数据是为一个示例维护的9倍缓存大小,所以TinyLFU的总元数据成本是每个缓存条目9·0.57 = 5.13字节。如果我们考虑到每个缓存条目应该包含一个需要11字节的视频ID,我们得出的结论是,TinyLFU能够大约记住比缓存大9倍的历史统计信息,而空间开销比只存储所有缓存项的键所需的空间开销要小。
为了进行比较,WLFU需要记住比缓存内容大9倍的显式历史。即使在空间效率最高的实现中,维护这个历史记录也需要花费每个缓存条目99个字节。此外,为了快速操作,需要对这些项进行显式摘要,因为遍历窗口并计算缓存项和替换候选项的频率非常慢。即使我们忽略了这个额外的内存开销,WLFU的准入策略仍然需要比TinyLFU多20倍的空间。
5.3 Caffeine实验
5.3.1 对比分析
Databases
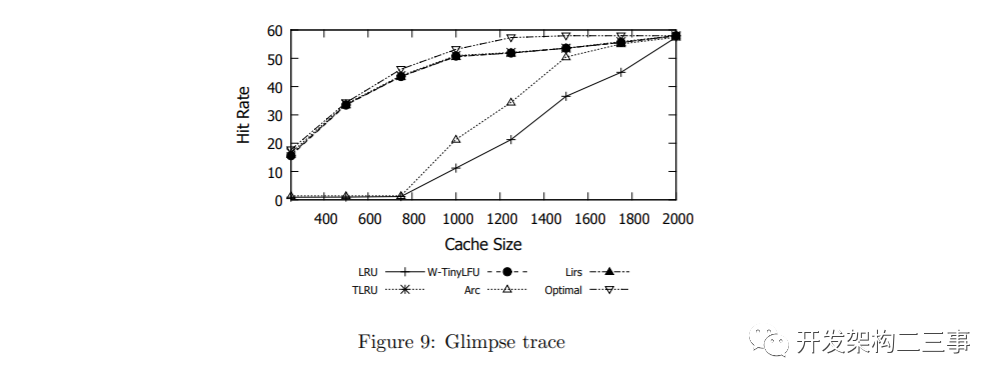
数据库图9和图10展示了TLRU和W-TinyLFU的命中率,并将其与ARC和LIRS最先进的方案进行了比较。在这两种轨迹中,TLRU和W-TinyLFU都提供了很好的结果。在Glimpse轨迹中,它们与LIRS相当,而在DS1轨迹中,TLRU和W-TinyLFU都优于所有其他策略。这表明TinyLFU方法对于各种类型的数据库都是一个可行的选择。
Windows File System
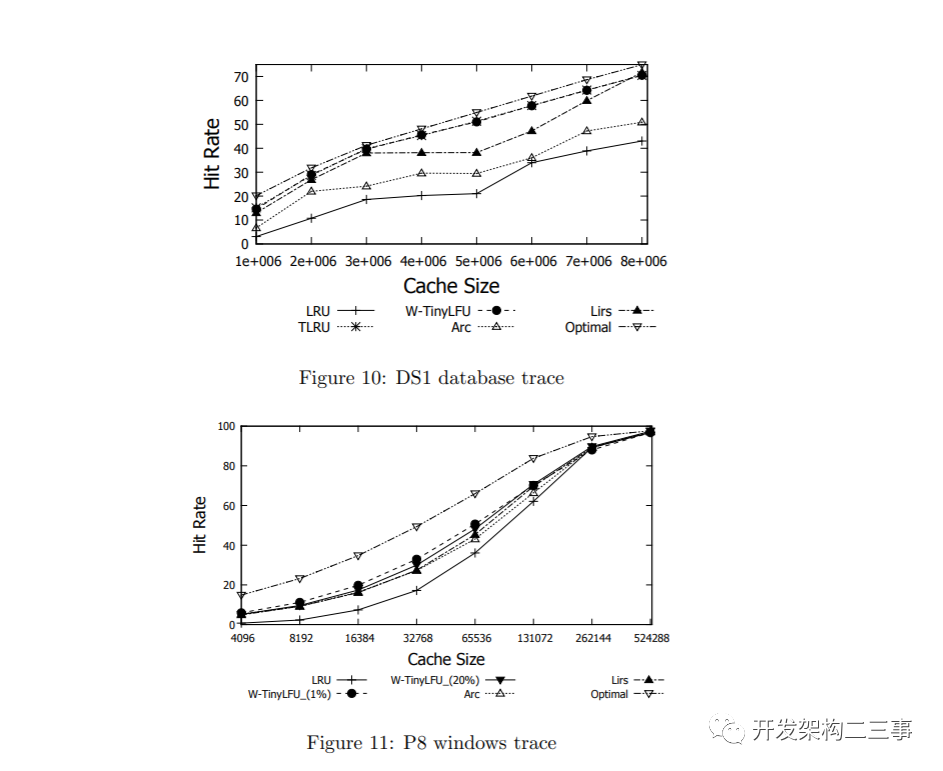
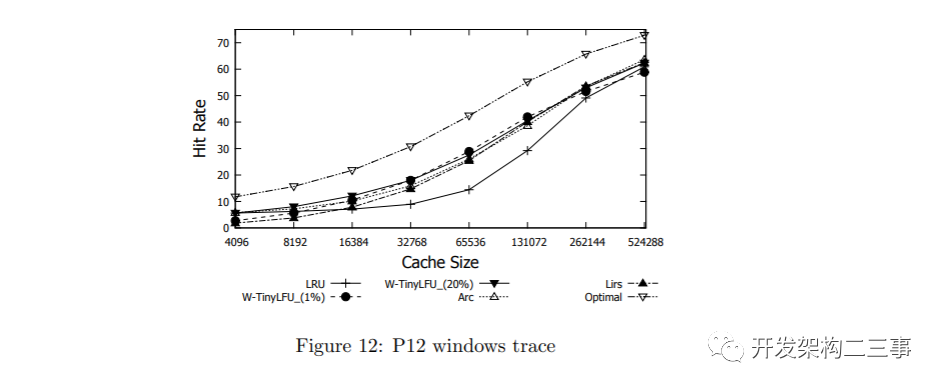
图11和12显示了windows工作站轨迹P8和P12[44]的结果。在这些轨迹中,我们使用1%的窗口缓存和20%的窗口缓存来评估W-TinyLFU。如图所示,除了最大数据点之外,这两种策略都实现了非常吸引人的命中率,并优于其他策略。在图12中,20%窗口缓存和1%窗口缓存的图形相交两次。这表明能够自适应地更改窗口缓存大小的潜在好处。
Disk Accesses in OLTP Systems
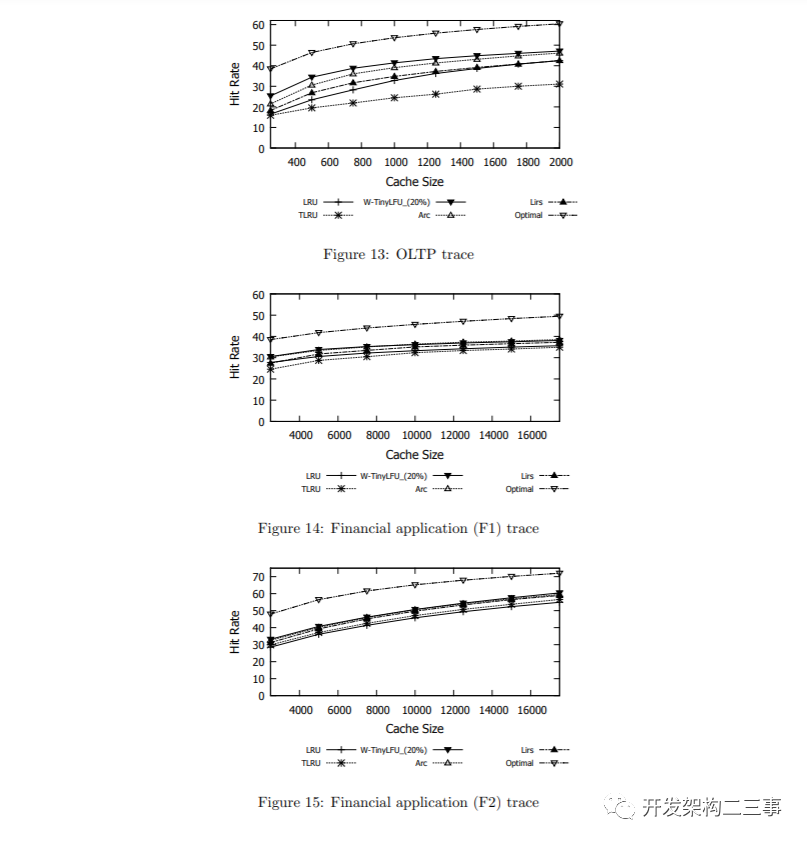
在图13所示的OLTP轨迹中,TinyLFU的表现很差,这是由于上述5.1节所报告的轨迹特性造成的。也就是说,顺序块访问的升序列表中散布了一些随机访问,这是由于偶尔的写重放或内存缓存丢失造成的。因此,TLRU不如其他的。图14和图15显示了来自运行金融应用程序[1]的服务器的两个额外OLTP轨迹的结果,暴露了类似的现象,但强度较低。也就是说,在最后两个数字中,所有方案之间的差异要小得多。
可以看出,在所有OLTP轨迹中,W-TinyLFU的性能可与先进水平相媲美。W-TinyLFU在这三个方面都优于LRU和LIRS。与ARC相比,W-TinyLFU在OLTP和F2轨迹略好,而在F1轨迹中,W-TinyLFU在较小的缓存大小上只比ARC好,两者之间有微小的差异。
SPC1-like
图16显示了从[44]获取的类似spc1的轨迹的结果。可以看到,TLRU和W-TinyLFU在该轨迹上的表现也优于所有其他策略。
Search Engine Queries
图17、18、19和20展示了W-TinyLFU和TLRU的行为以及来自[44,1]的各种搜索引擎轨迹。正如可以观察到的,在ARC和LIRS之间,ARC对于小的缓存更好,LIRS对于大的缓存更好。然而,TLRU和W-TinyLFU自始至终都比它们出色
在W-TinyLFU中调整窗口缓存大小
如上所述,对于大多数轨迹案例,W-TinyLFU具有窗口缓存,其大小为总缓存的1%,优于(或与)所有其他方案。相反,在OLTP、F1和F2中,TinyLFU通常性能不佳,尽管1%的窗口缓存大小提高了命中率,但它仍然不是性能最好的。在这些轨迹案例中,需要较大的窗口缓存。图21研究了窗口缓存和主缓存之间的缓存分配对W-TinyLFU在OLTP, F1和F2的命中率的影响。对于OLTP,我们测试了总缓存大小为1000项,而对于F1和F2,总缓存大小为2500项。正如可以观察到的,窗口缓存大小20 - 40%似乎在这些中表现最好。
5.4 误差的来源
TinyLFU中最明显的误差来源是由假阳性引入的近似精度。但是,在复位操作中执行整数除法而不是实数(浮点)除法也会导致截断错误。对于静态分布,测量采样误差也是可行的,也就是TinyLFU对下线分布的理解有多好。所有这些因素一起可以解释TinyLFU的(in)准确性。
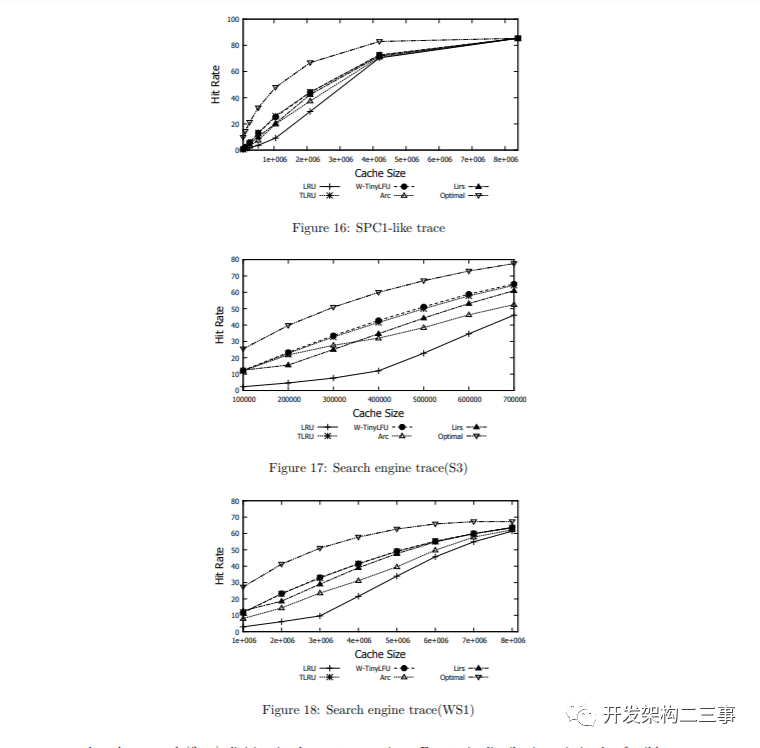
我们将采样误差定义为具有浮点计数器的精确TinyLFU的命中率与恒定分布下可达到的理想命中率之间的差。利用较大的样本容量可以降低静态分布的抽样误差。
接下来,截断错误是准确的TinyLFU(没有看门人和假正数)和浮点计数器与具有整数计数器的准确TinyLFU之间的命中率变化。这两种实现之间的唯一区别是在重置操作中执行的除法类型。通过允许计数器的更高计数(每个计数器的bit数更多),可以降低截断误差。
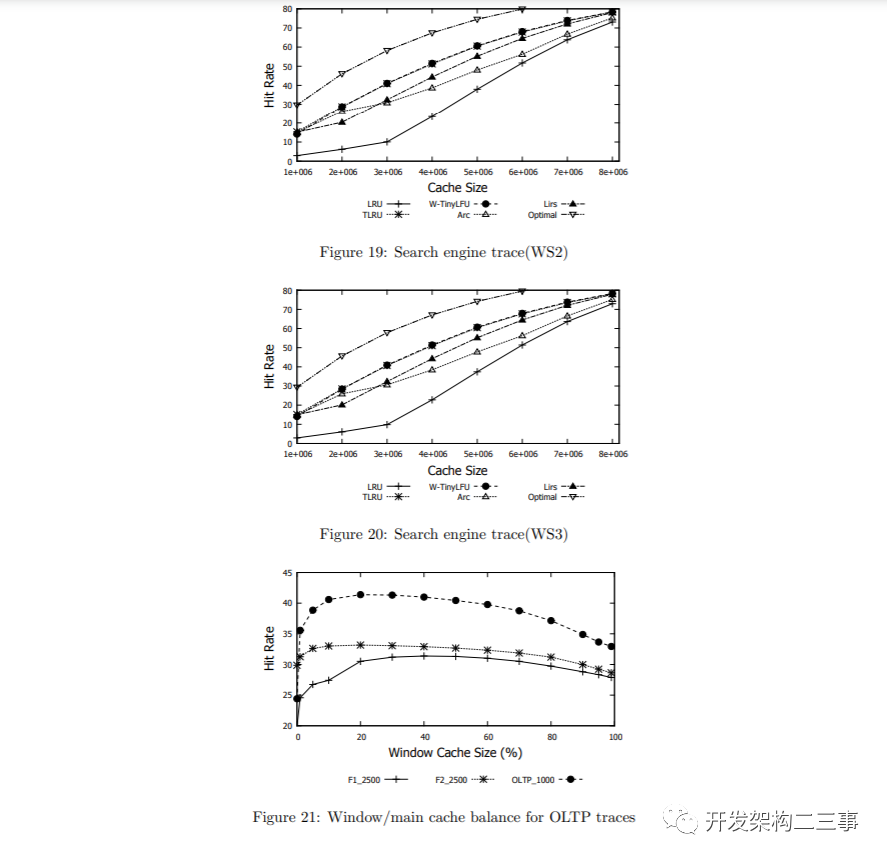
最后,近似误差是我们使用近似版本的TinyLFU(如本文所述)而不是精确版本获得的命中率之差。这意味着使用计数Bloom过滤器而不是散列表。命中率的差异是由于假阳性造成的,假阳性可能会扭曲采样,使不常见的项目出现频繁。
静态Zipf 0.9分布的结果显示在图22中。可以观察到,直到每个样本项有1.25字节时,近似误差才会出现。也就是说,TinyLFU的近似版本提供了与精确版本相同的命中率。正如预期的那样,在较小的样本容量下,截断误差更小,因此在9k个条目的样本中比在17k个条目的样本中更占优势。在17k样本中,截断误差几乎可以忽略不计。
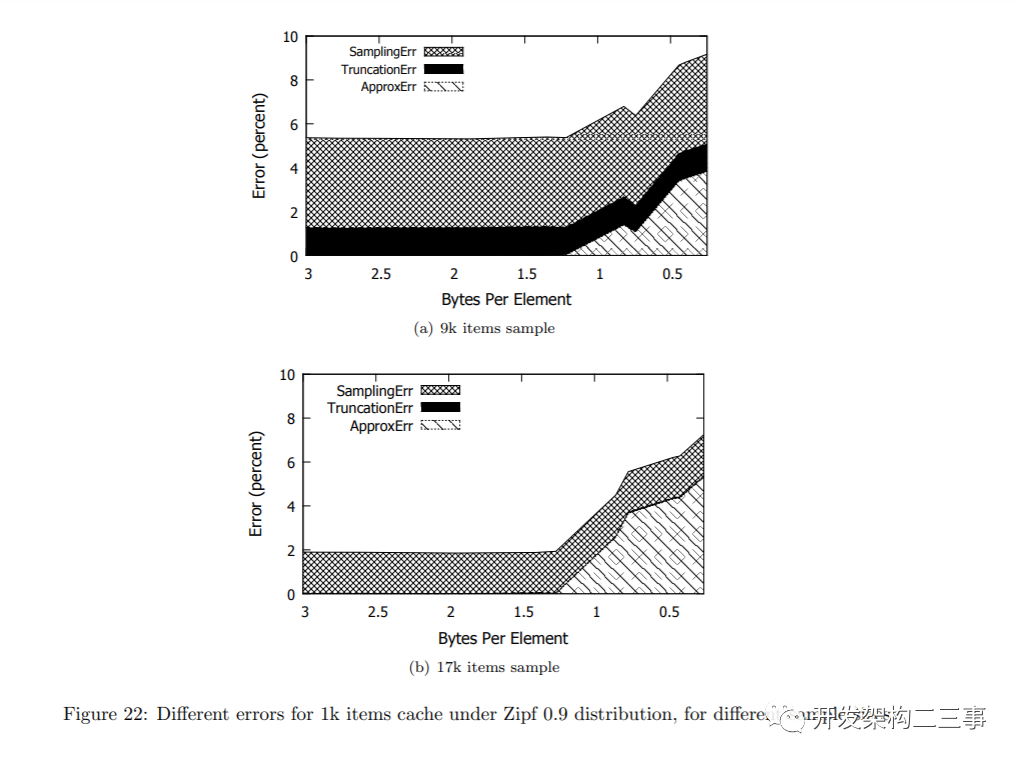
抽样误差是最棘手的一个,因为增加样本容量只有助于静态分布。样本容量越大,抽样误差越小。这种行为显然与实际工作负载不同,在实际工作负载中,样本量是根据经验的试错过程来选择的。
回想一下,TinyLFU在Caffeine中使用的是CM-Sketch,而不是计数Bloom过滤器。在其默认配置中,它为每个缓存条目分配8个字节,并维护一个示例大小是缓存大小的10倍。换句话说,每个元素使用0.8字节。通过将每个条目分配的空间加倍到16字节,在各种轨迹上获得的命中率增加了大约0.5%。换句话说,目前Caffeine的配置存在大约0.5%的近似误差。
结论
我们引入了TinyLFU,一种近似频率的缓存允许策略。我们证明了TinyLFU可以增加任意驱逐策略的缓存,并显著提高它们的性能。我们还优化了TinyLFU的内存消耗,使用了已知的近似计数技术和专门定制的新技术,以实现缓存的低内存占用。
与以前将ghost缓存条目合并到驱逐策略考虑事项的方案不同,在TinyLFU中,允许策略与驱逐策略是正交的。这种解耦遵循了关注点分离原则,简化了设计和实现,并允许分别进行优化。特别地,使用近似草图技术的录取策略能够维护一个相对大的样本的统计数据,而只消耗少量的元数据。
TinyLFU和它的变体W-TinyLFU的性能已经通过模拟进行了探索和验证,模拟使用了合成案例以及来自几个不同来源的多个真实世界案例。如前所述,TinyLFU是免费的开放源码,是CaffeineJava缓存项目[43]的一部分。展望未来,我们将研究一种基于简洁哈希表设计的改进实现[22,21]。
引用
•[1] Umass trace repository - http://traces.cs.umass.edu/index.php/Main/About.•[2] Martin Arlitt, Ludmila Cherkasova, John Dilley, Rich Friedrich, and Tai Jin. Evaluating content management techniques for web proxy caches. In In Proc. of the 2nd Workshop on Internet Server Performance, 1999.•[3] Martin Arlitt, Rich Friedrich, and Tai Jin. Performance evaluation of web proxy cache replacement policies. Perform. Eval., 39(1-4):149–164, February 2000.•[4] Hilla Atzmon, Roy Friedman, and Roman Vitenberg. Replacement policies for a distributed object caching service. In Confederated Int. Conf.s DOA, CoopIS and ODBASE, pages 661–674, 2002.•[5] G. Bianchi, E. Boschi, S. Teofili, and B. Trammell. Measurement data reduction through variation rate metering. In Proceedings IEEE INFOCOM, march 2010.•[6] G. Bianchi, S. Teofili, E. Boschi, B. Trammell, and C. Greco. Scalable and fast approximate excess rate detection. In Future Network and Mobile Summit, june 2010.•[7] Giuseppe Bianchi, Nico d’Heureuse, and Saverio Niccolini. On-demand time-decaying bloom filters for telemarketer detection. SIGCOMM Comput. Commun. Rev., 41(5):5–12, October 2011.•[8] Lee Breslau, Pei Cao, Li Fan, Graham Phillips, and Scott Shenker. Web caching and zipf-like distributions: Evidence and implications. In INFOCOM, pages 126–134, 1999.•[9] Yu Jin Cao, Jing, Aiyou Chen, Tian Bu, and Zhi-Li Zhang. Identifying high cardinality internet hosts. In IEEE INFOCOM, pages 810–818, 2009.•[10] Wei Koong Chai, Diliang He, Ioannis Psaras, and George Pavlou. Cache ”less for more” in information-centric networks. In Proceedings of the 11th international IFIP TC 6 conference on Networking, pages 27–40. Springer-Verlag, 2012.•[11] Kai Cheng and Yahiko Kambayashi. Lru-sp: A size-adjusted and popularity-aware lru replacement algorithm for web caching. In 24th IEEE Int. Computer Software and Applications Conf. (COMPSAC), pages 48–53, 2000.•[12] Xu Cheng, C. Dale, and Jiangchuan Liu. Statistics and social network of youtube videos. In 16th Int. Workshop on Quality of Service (IWQoS), pages 229–238, june 2008.•[13] Ludmila Cherkasova. Improving www proxies performance with greedy-dual-size-frequency caching policy. Technical report, In HP Tech. Report, 1998.•[14] Gregory Chockler, Guy Laden, and Ymir Vigfusson. Data caching as a cloud service. In Proc. of the 4th ACM International Workshop on Large Scale Distributed Systems and Middleware (LADIS), pages 18–21. ACM, 2010.•[15] Gregory Chockler, Guy Laden, and Ymir Vigfusson. Design and implementation of caching services in the cloud. IBM Journal of Research and Development, 55(6):9:1–9:11, 2011.•[16] Baek-Young Choi, Jaesung Park, and Zhi-Li Zhang. Adaptive random sampling for load change detection. SIGMETRICS Perform. Eval. Rev., 30(1):272–273, June 2002. 20•[17] Saar Cohen and Yossi Matias. Spectral bloom filters. In Proc. of the ACM SIGMOD Int. Conf. on Management of data, pages 241–252, 2003.•[18] Graham Cormode and S. Muthukrishnan. An improved data stream summary: The count-min sketch and its applications. J. Algorithms, 55:29–38, 2004.•[19] Xenofontas Dimitropoulos, Marc Stoecklin, Paul Hurley, and Andreas Kind. The eternal sunshine of the sketch data structure. Comput. Netw., 52(17):3248–3257, December 2008.•[20] G. Einziger, B. Fellman, and Y. Kassner. Independent counter estimation buckets. In IEEE Conference on Computer Communications (INFOCOM), pages 2560–2568, 2015.•[21] G. Einziger and R. Friedman. Tinyset - an access efficient self adjusting bloom filter construction. In 24th International Conference on Computer Communication and Networks (ICCCN), Aug 2015.•[22] G. Einziger and R. Friedman. Counting with TinyTable: Every bit counts! In 17th International Conference on Distributed Computing and Networking (ICDCN), 2016.•[23] Gil Einziger and Roy Friedman. A formal analysis of conservative update based approximate counting. In International Conference on Computing, Networking and Communications (ICNC), pages 255–259, 2015.•[24] Gil Einziger, Roy Friedman, and Yoav Kantor. Shades: Expediting kademlias lookup process. In Euro-Par, Lecture Notes in Computer Science, pages 391–402. 2014.•[25] Cristian Estan, Ken Keys, David Moore, and George Varghese. Building a better netflow. SIGCOMM Comput. Commun. Rev., 34(4), August 2004.•[26] Cristian Estan and George Varghese. New directions in traffic measurement and accounting. SIGCOMM Comput. Commun. Rev., 32(4):323–336, August 2002.•[27] Li Fan, Pei Cao, Jussara Almeida, and Andrei Z. Broder. Summary cache: a scalable wide-area web cache sharing protocol. IEEE/ACM Trans. Netw., 8(3):281–293, June 2000.•[28] Brad Fitzpatrick. Distributed caching with memcached. Linux J., 2004(124):5–, August 2004.•[29] Phillipa Gill, Martin Arlitt, Zongpeng Li, and Anirban Mahanti. Youtube traffic characterization: a view from the edge. In Proc. of the 7th ACM SIGCOMM Conf. on Internet measurement (IMC), pages 15–28, 2007.•[30] Amit Goyal, Hal Daum´e, III, and Graham Cormode. Sketch algorithms for estimating point queries in nlp. In Proc. of the Joint Conf. on Empirical Methods in Natural Language Processing and Computational Natural Language Learning, pages 1093–1103, 2012.•[31] Amit Goyal and Hal Daumea´e; III. Lossy conservative update (lcu) sketch: Succinct approximate count storage. In Proc. of the 25th AAAI Conf. on Artificial Intelligence, 2011.•[32] Amit Goyal, Jagadeesh Jagarlamudi, Hal Daum´e, III, and Suresh Venkatasubramanian. Sketching techniques for large scale nlp. In Proc. of the 6th NAACL HLT Web as Corpus Workshop, WAC, pages 17–25, 2010.•[33] John L. Hennessy and David A. Patterson. Computer Architecture - A Quantitative Approach (5. ed.). Morgan Kaufmann, 2012.•[34] Chengchen Hu, Bin Liu, Hongbo Zhao, Kai Chen, Yan Chen, Chunming Wu, and Yu Cheng. Disco: Memory efficient and accurate flow statistics for network measurement. In Proc. of the 30th IEEE International Conference on Distributed Computing Systems, ICDCS, pages 665–674, 2010.•[35] Chengchen Hu, Sheng Wang, Jia Tian, Bin Liu 0001, Yu Cheng, and Yan Chen. Accurate and efficient traffic monitoring using adaptive non-linear sampling method. In INFOCOM, pages 26–30. IEEE, 2008. 21•[36] Song Jiang and Xiaodong Zhang. Lirs: An efficient low inter-reference recency set replacement policy to improve buffer cache performance. ACM SIGMETRICS, pages 31–42, 2002.•[37] Theodore Johnson and Dennis Shasha. 2q: A low overhead high performance buffer management replacement algorithm. In Proc. of the 20th Int. Conf. on Very Large Data Bases (VLDB), pages 439–450, 1994.•[38] G. Karakostas and D. N. Serpanos. Exploitation of different types of locality for web caches. In Proc. of the 7th Int. Symposium on Computers and Communications (ISCC), 2002.•[39] Ramakrishna Karedla, J. Spencer Love, and Bradley G. Wherry. Caching strategies to improve disk system performance. IEEE Computer, 1994.•[40] Anirban Ketan Shah and Mitra Dhruv Matani. An o(1) algorithm for implementing the lfu cache eviction scheme. Technical report, 2010. ”http://dhruvbird.com/lfu.pdf”.•[41] Piotr Kolaczkowski. Memory efficient algorithm for mining recent frequent items in a stream. In Proc. of the international conference on Rough Sets and Intelligent Systems Paradigms, RSEISP, pages 485–494, 2007.•[42] Yi Lu, Andrea Montanari, Balaji Prabhakar, Sarang Dharmapurikar, and Abdul Kabbani. Counter braids: a novel counter architecture for per-flow measurement. In Proc. of the ACM SIGMETRICS Int. Conf. on Measurement and modeling of computer systems, pages 121–132, 2008.•[43] Ben Manes. Caffeine: A high performance caching library for java 8. https://github.com/benmanes/caffeine.•[44] Nimrod Megiddo and Dharmendra S. Modha. Arc: A self-tuning, low overhead replacement cache. In Proc. of the 2nd USENIX Conf. on File and Storage Technologies (FAST), pages 115–130, 2003.•[45] Nimrod Megiddo and Dharmendra S. Modha. System and method for implementing an adaptive replacement cache policy. US Patent 6996676, February 7, 2006.•[46] S. Narayanasamy, T. Sherwood, S. Sair, B. Calder, and G. Varghese. Catching accurate profiles in hardware. In The 9th International Symposium on High-Performance Computer Architecture (HPCA), pages 269 – 280, feb. 2003.•[47] Elizabeth J. O’Neil, Patrick E. O’Neil, and Gerhard Weikum. The lru-k page replacement algorithm for database disk buffering. ACM SIGMOD Rec., 22(2):297–306, June 1993.•[48] Stefan Podlipnig and Laszlo B¨osz¨ormenyi. A survey of web cache replacement strategies. ACM Comput. Surv., 35(4):374–398, December 2003.•[49] Ioannis Psaras, Wei Koong Chai, and George Pavlou. Probabilistic in-network caching for information-centric networks. In Proceedings of the second edition of the ICN workshop on Information-centric networking, pages 55–60. ACM, 2012.•[50] Frederic Raspall and Sebastia Sallent. Adaptive shared-state sampling. In Proceedings of the 8th ACM SIGCOMM conference on Internet measurement, IMC, pages 271–284, 2008.•[51] Dimitrios N. Serpanos and Wayne H. Wolf. Caching web objects using zipf’s law. pages 320–326, 1998.•[52] Rade Stanojevic. Small active counters. In 26th IEEE Int. Conf. on Computer Communications (INFOCOM), pages 2153–2161, 2007.•[53] Geetika Tewari and Kim Hazelwood. Adaptive web proxy caching algorithms. Technical Report TR-13-04, ”Harvard University”, 2004.•[54] Erez Tsidon, Iddo Hanniel, and Isaac Keslassy. Estimators also need shared values to grow together. In INFOCOM, pages 1889–1897, 2012. 22•[55] Guido Urdaneta, Guillaume Pierre, and Maarten van Steen. Wikipedia workload analysis for decentralized hosting. Elsevier Computer Networks, 53(11):1830–1845, July 2009.•[56] Stephen Williams, Marc Abrams, and Charles R. Standridge. Removal policies in network caches for world-wide web documents, 1996.•[57] Neal Young. On-line caching as cache size varies. In Proc. of the second annual ACM-SIAM symposium on Discrete algorithms (SODA), pages 241–250, 1991•http://highscalability.com/blog/2016/1/25/design-of-a-modern-cache.html
References
[1]
CountMin Sketch: http://dimacs.rutgers.edu/~graham/pubs/papers/cmsoft.pdf[2]
8: 以更大的元数据为代价[3]
44: 如下所示为spc1






