PriorityQueue是比较特殊的队列,它继承自Queue的接口,但是它并不是FIFO先入先出,它是经过排序过的队列,
也就是最大(或者最小)值是放在队列的队头处,具体面对的场景是求Top K的问题;
对于PriorityQueue,它依然有add,poll这些接口,和其他的Queue一样,但是和util包的大多数类一样,也是线程不安全的;
下面分析一下PriorityQueue的源码。
1.堆的数据结构实现
PriorityQueue的接口是Queue的,但是其实现的数据结构却是一个堆,可以这么说,“挂着羊头卖狗肉”,
使用堆的目的是为了解决优先队列当中的“优先”问题,因为堆的作用就是求这一串值中的最大值和最小值,
当为最大值的时候,这个堆就是最大堆,当为最小值的时候,这个堆就是最小堆;
我们可以来看一个最小堆的实例:
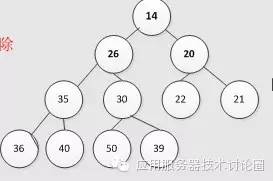
这就是一个典型的堆,
使用数组来表示就是Object array[] = {14,26,20,35,30,22,21,36,40,50,39};按照顺序来进行表示
之所以称之为堆,是因为其满足下列的公式:
ki≤K2i且ki≤K2i+1(最小堆) 或 (2)Ki≥K2i且ki≥K2i+1 (最大堆)
上述的意思也就是只要是父节点,肯定比起两个子节点要小,===》而这也是堆的特性;
一定注意的一点是,最小堆不能保证你的左子树比右子树要小,可以看到上图中的堆,右子树20,22,21比左子树最小的都小,
但这个数据结构仍旧是一个最小堆,
===》这里再一次证明了,最小堆数据结构的本意在于,就是选出一个最小的做为父节点,而不管兄弟节点的大小;
===》因此,最小堆保证了,从上到下都是逐步增大的,这个趋势是肯定保证的,而最小的节点在最顶部;
PriorityQueue通过最小堆这种数据结构,来实现优先队列,也正是利用其 Top K这一个概念;
对于堆的存储结构,使用的就是普通的数组:

为什么不使用链表呢?
==》毕竟链表作为Node节点组装成一个堆,肯定是没有问题的,
但是,堆中大量的调整排序堆化等操作,这些操作都是需要递归遍历的
这种方式的效率很低;
如果换做是用数组的话,可以看一下程序,例如求一个节点的父节点:
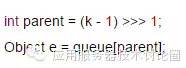
直接通过数组的位移直接可以定位到父节点,这仅仅是一个例子,
除此之外很多定位完全可以通过位运算和位移搞定,效率极高,这也就是数组经常被用于优先队列的原因;
我们来看一个从Collection中导入到优先队列的构造方法:

根据传入的参数类型,一共分成三种情况,
a.如果是已经排序过的SortSet,不但能满足堆的需求,而且还能保证左子树比右子树要小,这个是平衡二叉排序树的需求了,
如果是这种情况的话,那么直接将Set,使用Arrays.copy进行拷贝到queue数组中;
b.如果就是PriorityQueue的话,没啥可说的,那么直接就可以进行赋值,
c.如果连排序的Collection都不是的话,那么就需要首先堆化,这个也就是调用的heapify方法了;
所谓的堆化,实质就是堆排序,以最大堆的算法为例:
1)将初始待排序关键字序列(R1,R2....Rn)构建成大顶堆,此堆为初始的无须区;
2)将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n];
3)由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
上述的思路其实很简单,目的是最大堆,那么每一次划分两个区域,先将栈顶放到最后,然后调整除了栈顶的其余的元素,进行siftUp,挨个比较
直到在这个区域确定一个最大的,再和原来的栈顶进行比较,哪个大将哪个放到最终的栈顶位置,===》这样第一轮就可以确定栈顶,也就是最大的元素;
其次,逐步按照这个思路,每一次确定一个其次最大的,再其次最大的... ...
这样下来,整个堆的雏形也建立起来了,这就是堆化;
具体的实现的思路是:

heapify的每一轮直接确定一个最小的位置,调用的方法是siftDown方法,传入的是最后一个节点
siftDown方法含有一个比较器的方法,另外一个是默认的最小堆的算法
siftDownComparable是最小堆的算法,while循环,每一次把除了最后一个节点的剩余的节点中,找到一个最小值,
赋值给queue[k],这样就确定了一个位置,
上述的流程循环往复,每一次不断的确定位置,这样确定位置的元素越来越多,一直到最终只剩1个节点,那么最后这个节点肯定就是最大的;
到此为止,堆化完成,整个数据结构就是一个最小堆;
2.add
既然堆结构应完成了,那么就看看如何在堆的结构下,来完成队列的相关实现逻辑;
下面分析一下增加元素,add:

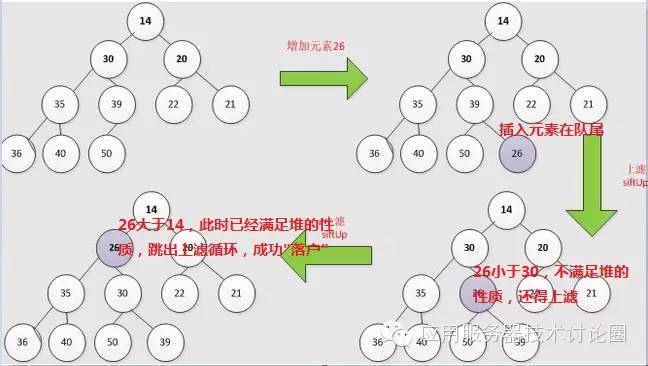
整个add方法的思路主要在siftUp上,它的作用首先是将元素插到队尾,然后不断的进行“上滤”操作,
也即是当前插入元素不断的与父节点比较大小,
因为堆的性质务必保证父节点比子节点小,只要当前节点小于父节点,说明还得继续调整堆,
一直到当前插入节点比父节点大才行,这个时候当前节点就已经成功"落户",插入完成;
这个思路可以使用下面的图来进行描述:
3.poll/peek/remove
peek方法是查看一下堆顶元素,但是不删除堆顶元素,直接返回,这个比较简单:

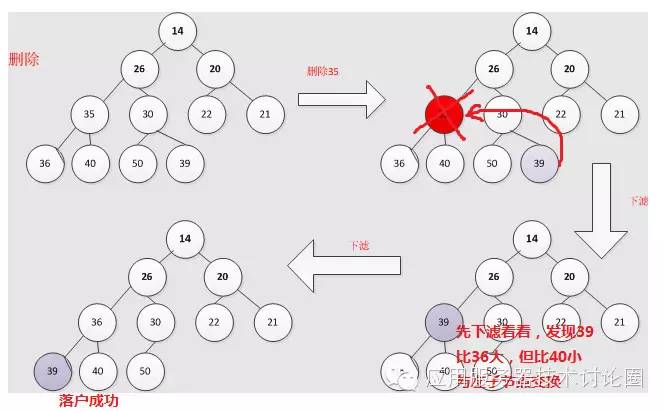
比较复杂的是poll出队,因为堆顶元素弹出之后,堆不完整了,这个时候算法是把最后一个元素填补到栈顶,
因为这个时候队尾元素肯定非常大,它现在在栈顶,这个时候堆已经不是堆了,
必然不满足最小堆的条件,所以需要得进行堆化,
按照这个思路推断,整体思路和堆化差不太多:

这里和heapify几乎差不多,因为栈顶元素比较大,所以需要的是siftDown操作,已经分析过其实现,
整体的示意图为:
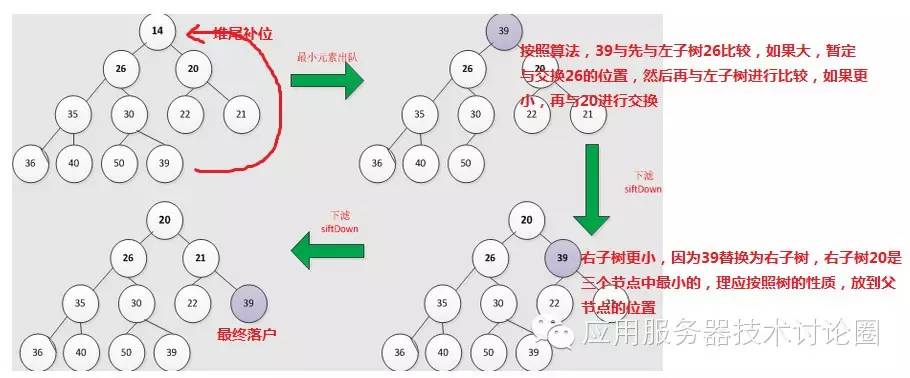
对于而需要与add方法区分的是,siftDown是栈顶元素偏大,所以需要向下比较,一直到当前节点比两个子节点都小,那么落户成功;
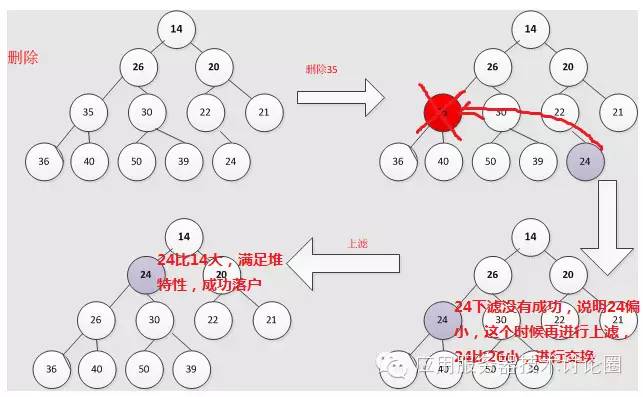
而siftUp是当前节点在队尾,队尾元素偏小,需要向上比较,一直到合适的成功的位置;
这两个运动是相反的,整体思路其实都差不多,就是比较,当当前比较节点与父节点或者两个子节点,在局部满足堆的特性,比较结束,节点落户;
这一次的整个操作就相对结束了;
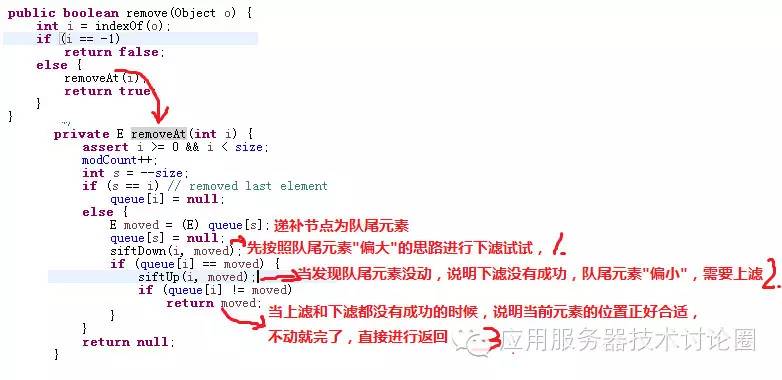
对于删除节点来说,也就是remove方法,思路和前面一样,也是队尾元素补进来,
但是因为删除的节点可能在堆的中间位置,堆的特性只是满足堆顶元素是最大值或者最小值,
但是不能满足左右子树的大小关系均匀,也就是说左子树第2层的节点可能比右子树的第n层节点还大,
这种情况导致的因为删除元素可能有两种情况,
a.删除节点的递补队尾元素偏大
b.删除节点的递补队尾元素偏小
这两种情况,因此基于上述情况,一个是进行上滤,一个是进行下滤,可以分析源码:
整体的示意图为:
第一种情况为:
第二种情况:
关于add,peek,poll,remove这几个方法是堆相关的算法,也是优先队列最为关键的方法,务必掌握,
其他的几个方法,如index

就是逐个对queue数组进行遍历,和contains,甚至iterator都差不多,这里就不再进行缀余;
5.线程不安全
最后,值得一提的还是线程不安全,因为在util包中,大多数数据结构都还是单线程运作,
前面分析源码中的:
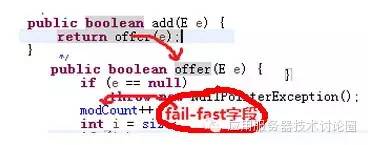
modCount字段,和其他的数据结构类似,也是在迭代的过程中进行修改,会产生并发修改异常,
可以看一下这个优先队列中的迭代器实现:
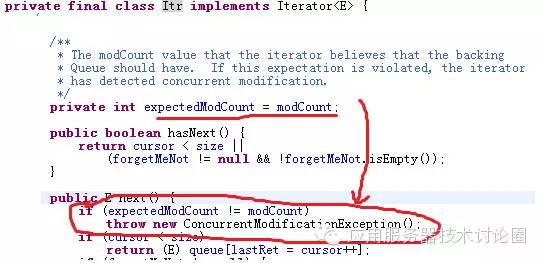
在Util包中的解决办法,还是使用Collections的同步方法,因为优先队列是Collection,所以使用:
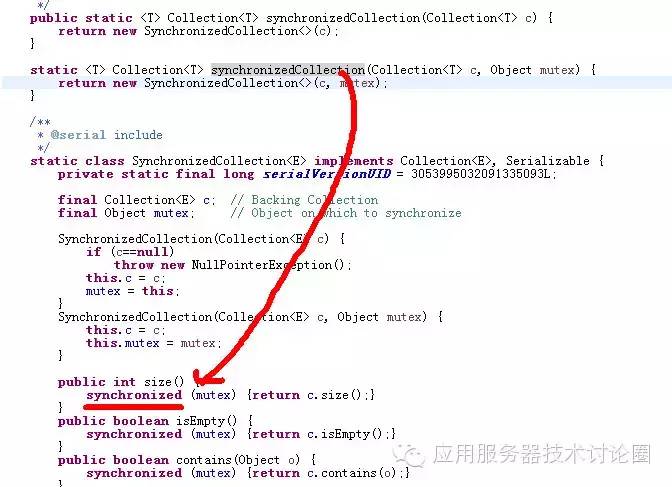
思路也是代理模式,用synchronized进行包装;
替代方案,也是并发包中的Concurrent优先队列
总结:
PriorityQueue是用最小堆来实现队列,
利用最小堆的栈顶元素肯定是整个序列中最小的来满足"优先"的需求!






