哈夫曼树的定义
给树中结点赋予一个表示某种意义的数组,称为该结点的权。
从树根到任意结点的路径长度(经过的边数)与该结点上权值的乘积,称为该结点的带权路径长度。
一棵树中的所有叶子结点的带权路径长度之和称为该树的带权路径长度(WPL)。
带权路径长度WPL最小的二叉树称为哈夫曼树,也叫最优二叉树。
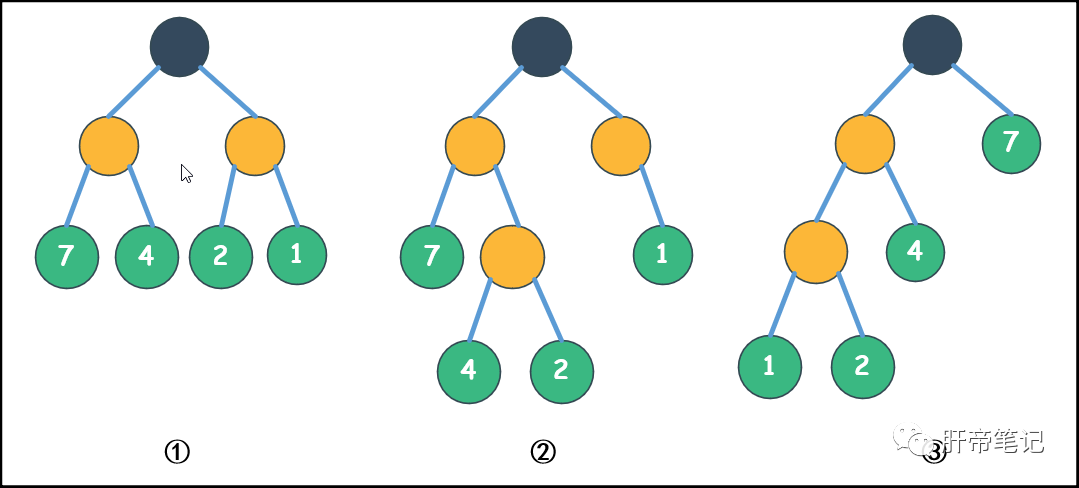
① WPL:7 × 2 + 4 × 2 + 2 × 2 + 1 × 2 = 28
② WPL:4 × 3 + 2 × 3 + 7 × 2 + 1 × 2 = 34
③ WPL:1 × 3 + 2 × 3 + 4 × 2 + 7 × 1 = 24
第三个二叉树是哈夫曼树,也就是最优二叉树。
哈夫曼树的构造
给定一些结点,根据其权值构造一个哈夫曼树。
构造步骤
给定一个数组{ 20, 25, 2, 3, 6, 7, 10, 45 }
,构建一个哈夫曼树。下面是步骤:
先将结点池中的结点按照权值从小到大排序:{ 2, 3, 6, 7, 10, 20, 25, 45 }
。
先拿出权值最小的两个结点出来,组成一棵树。然后将这两个结点的权值相加,作为父结点的权值。最后将父结点放到结点池中。
>>步骤1<<:拿出2和3,创建一个新的结点权值为2 + 3 = 5,组成一棵树。再将父结点权值放入池中,此时:{ 5, 6, 7, 10, 20, 25, 45 }
。
>>步骤2<<:拿出5和6,父结点5 + 6 = 11。放入池中:{ 7, 10, 11, 20, 25, 45 }
。
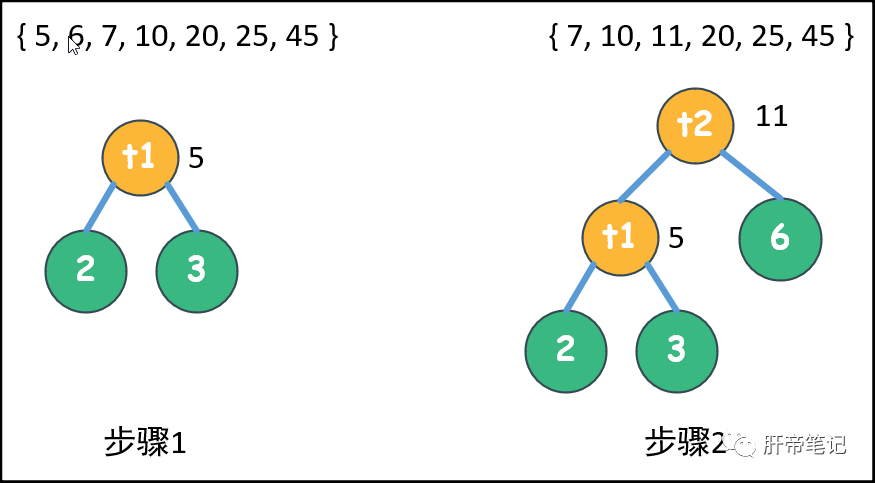
>>步骤3<<:拿出7和10,父结点17,放入池中。{ 11, 17, 20, 25, 45 }
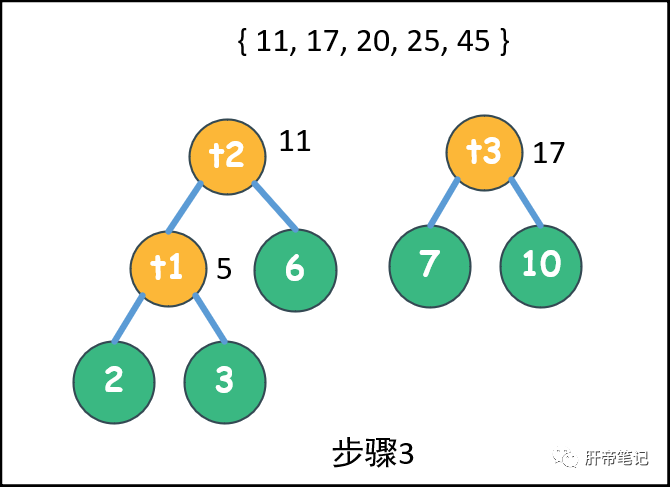
>>步骤4<<:拿出11和17,父结点28,放入池中:{ 20, 25, 28, 45 }
。
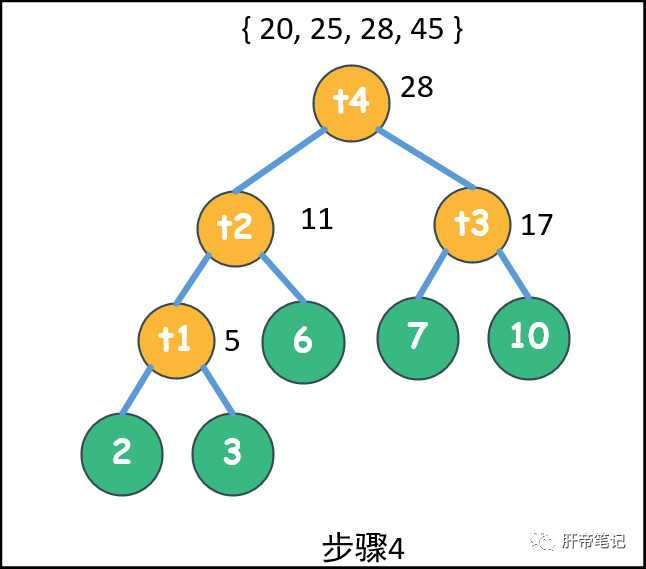
>>步骤5<<:拿出20和25,父结点45,放入池中:{ 28, 45, 45 }
。
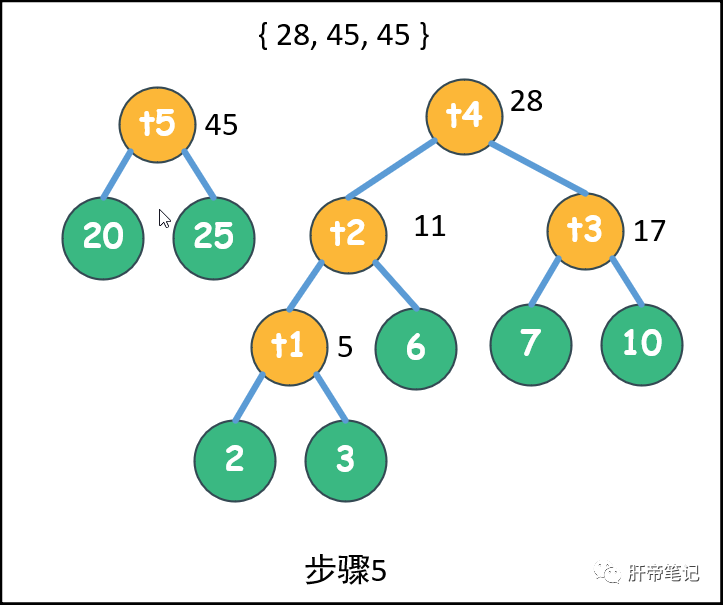
>>步骤6<<:获取28和45,父结点73,放入池中:{ 45, 73 }
。
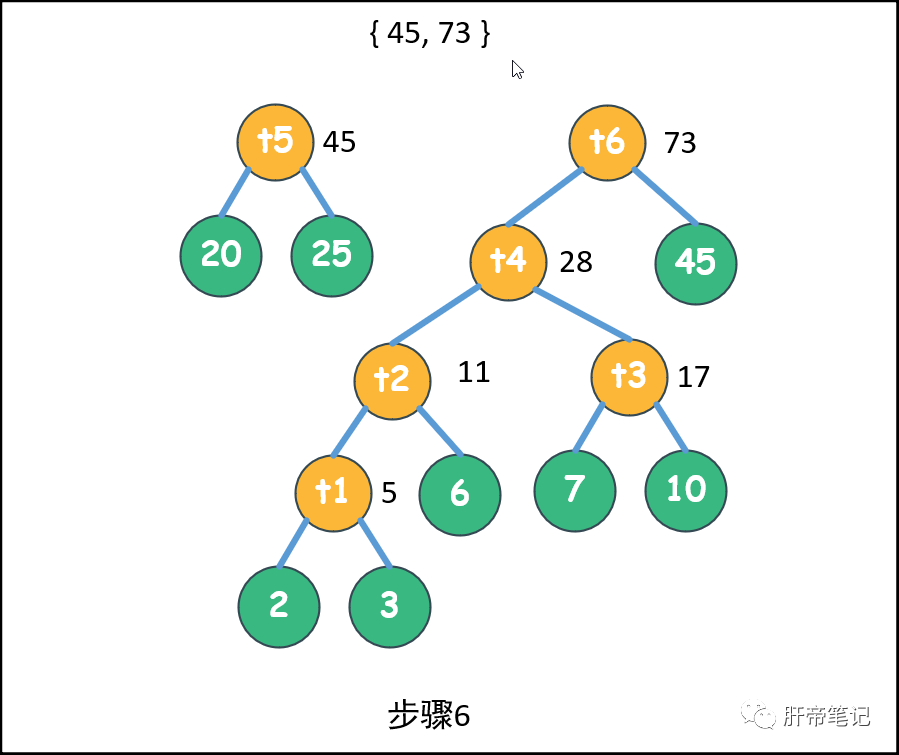
>>步骤7<<:拿出45和73,父结点118,放入池中:{ 118 }
。此时池中只有一个元素,那么哈夫曼树构造完毕,最后一个元素就是树根了。
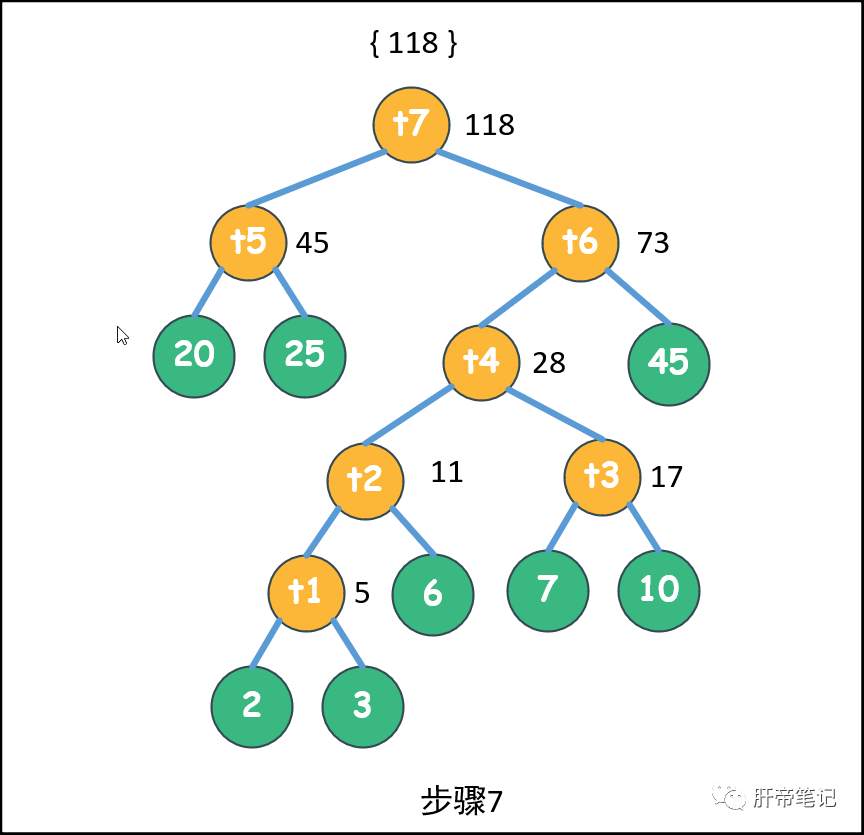
❝哈夫曼树的形态不止一种,但是他们的WPL都是最小的。
代码实现
>>结点对象<<
实现Comparable接口,是为了方便我们对集合按照权值大小进行排序。
/**
* 二叉树的结点对象
*/
class TreeNode implements Comparable<TreeNode> {
/**
* 权值
*/
private int weight;
/**
* 左子树指针
*/
private TreeNode left;
/**
* 右子树指针
*/
private TreeNode right;
/**
* 该结点表示的字符
*/
private char value;
// 省略get set
// 省略构造方法
/**
* 按照权值升序
*/
@Override
public int compareTo(TreeNode node) {
return this.weight - node.weight;
}
}
>>构造哈夫曼树的方式一<<
/**
* 给定一个int数组,构造一个哈夫曼树
* 使用List集合,但是需要自己排序
* {19,21,2,3,6,7,10,32}
*
* @param array
* @return
*/
public void buildHuffmanTree1(int[] array) {
// 初始化结点
ArrayList<TreeNode> nodes = Arrays.stream(array)
.mapToObj(TreeNode::new)
.collect(Collectors.toCollection(ArrayList::new));
// 当nodes集合中只剩下最后一个结点时,表明哈夫曼树构建成功
while (nodes.size() > 1) {
// 先将集合按照从小到大排序
Collections.sort(nodes);
// 拿出最小的两个元素,并将其删除
TreeNode left = nodes.remove(0);
TreeNode right = nodes.remove(0);
// 创建一个新的结点
TreeNode father = new TreeNode(left.weight + right.weight);
father.left = left;
father.right = right;
// 将新的结点放入集合中
nodes.add(father);
}
// 哈夫曼树的根结点
root = nodes.remove(0);
}
>>构造哈夫曼树的方式二<<
什么?还要用List自己排序,太麻烦了,使用优先队列PriorityQueue吧!
**
* 给定一个int数组,构造一个哈夫曼树
* <p>
* 什么 还要用List自己排序,太麻烦了,使用优先队列{@linkplain java.util.PriorityQueue}吧
* {19,21,2,3,6,7,10,32}
*
* @param array
* @return
*/
public void buildHuffmanTree2(int[] array) {
// 初始化结点 放到优先队列中,添加元素到该队列会自动按照实现的Comparable接口排序出队
PriorityQueue<TreeNode> queue = Arrays.stream(array)
.mapToObj(TreeNode::new)
.collect(Collectors.toCollection(PriorityQueue::new));
while (queue.size() > 1) {
// 拿出两个元素
TreeNode left = queue.poll();
TreeNode right = queue.poll();
// 创建一个新的结点
TreeNode father = new TreeNode(left.weight + right.weight);
father.left = left;
father.right = right;
// 将新的结点放入优先队列中
queue.offer(father);
}
// 哈夫曼树的根结点
root = queue.poll();
}






