如何实现归并排序

今天介绍归并排序，归并排序采用经典的分治法思想，将大规模的待排序数组，划分为小规模进行排序。

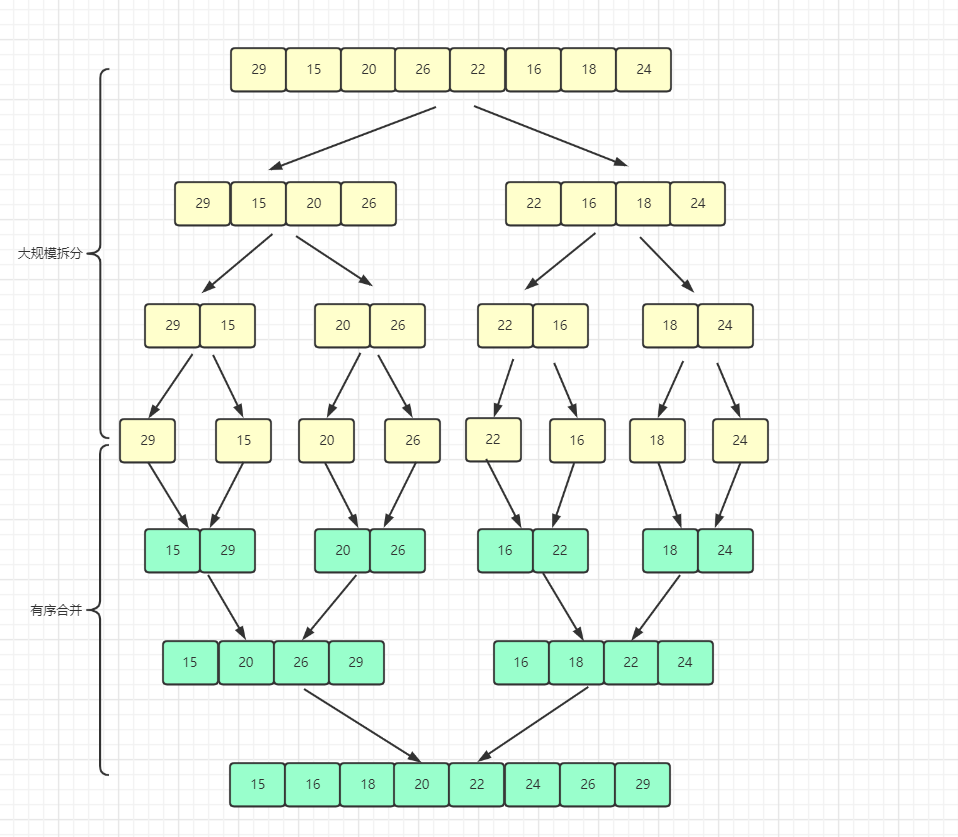
先将数组二分，直到只剩下一个元素时，不用再划分，因为一个元素是有序的。

然后向上合并，合并的新规模也是有序的，直到合并至原规模大小，此时数组已有序。

归并排序不是原地算法，因为在合并时，需要借助额外的数组空间来完成合并操作。

在合并两个子数组时，需要的额外数组空间最大为左子数组的长度。

所以在初始化数组空间时，需要注意长度，预留足够的空间。

例如数组长度为10，需要预留多少的额外空间呢？

根据第一次二分数组得出左子数组坐标从0到4，4是通过（0+9）/2得出。所以预留的长度应该是5。

如果数组长度为9，又需要预留多少的额外空间呢？

根据二分数组得出左子数组坐标从0到4，4是通过（0+8）/2得出。所以预留的长度也是5。

也就是预留长度是数组长度除于2并向上取整。

而length>>1是向下取整，所以我们可以通过(length+1>>1)进行向上取整。

对于整个归并排序，核心的步骤还是在于合并的阶段。

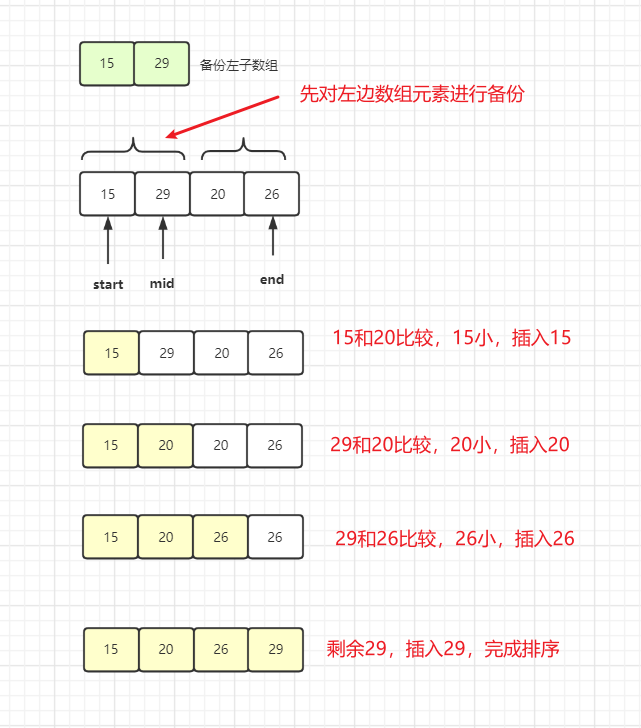
先进行左子数组的备份，因为后面进行比较时，都将数组从左开始填充。

遍历的结束是遍历完左子数组，那右子数组不需要遍历完吗？

当遍历完左子数组时，说明左子数组都被填充完了，此时右子数组的元素肯定都比填充的大，而且右子数组原本就有序，就不用再遍历了。

什么时候从左子数组中取出元素进行填充呢？

当右子数组都遍历完或者遍历的右子数组元素比左子数组的元素大时，使用左子数组遍历的元素进行填充。

归并排序的时间复杂度为O(nlogn)，因为需要额外空间，且与待排序的数组规模有关，空间复杂度为O(n)。