论文学习笔记：FLOD

写在前面

今天分享一篇论文学习笔记。

论文：

《FLOD:Oblivious Defender for Private Byzantine-Robust Federated Learning with Dishonest-Majority》

作者：董业

链接：Cryptology ePrint Archive: Report 2021/993

https://eprint.iacr.org/2021/993.pdf

在联邦学习在即解决拜占庭问题同时也要保护隐私数据是一个矛盾的问题。一方面，隐私数据保护要求禁止访问单个模型数据，或者说不能够区分各个模型之间的数据；而解决拜占庭问题则需要对全体模型数据进行数学分析从而将异常数据从正常数据中区分出来。此外现有的这方面技术也是基于诚实大多数场景假设的。本文提出了FlOD方法，基于汉明距离的方法实现对异常数据的处理，同时使用基于布尔秘密分享的方法实现安全的的两方聚合方案，从而实现了在恶意大多数场景下对上述矛盾问题的解决。经实验验证本方案在能够抵抗现有的拜占庭攻击同时损失很小的精度，此外相比较于ABY-AHE方案在离线阶段有两倍的性能提升，相比较于FLGuard有167倍以上的通信开销和3.1倍以上的运行时间开销。

预备知识

基本知识

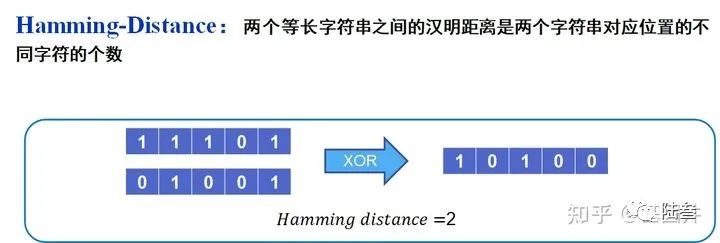
预备知识包括联邦学习、推理攻击、拜占庭攻击和汉明距离，联邦学习、推理攻击和拜占庭攻击相信大家已经很熟悉了，所以在这里给大家简单介绍汉明距离，如下图所示：

此外还需要了解一下SignSGD：

最后还要了解一下前人的工作FLTrust：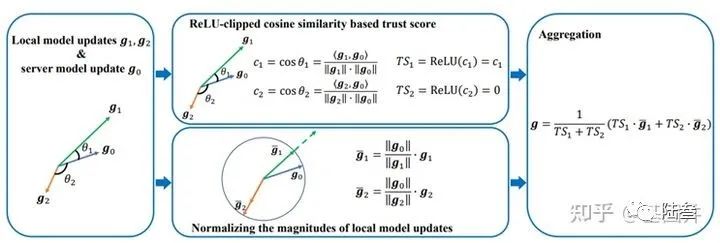

密码学知识：

包括2PC的安全计算和同态加密的基本知识。

FLOD方案

FLOD和FLTrust类似，依旧再服务器端保存一部分的训练数据Root Dataset，这个训练集可以很小，但是必须是干净的，目的就是提供一个绝对安全的参考值用来判定其他梯度向量是否异常。而且FLOD方案是可以抵御恶意大多数的拜占庭攻击的。接下来就来看看基础方案的整体设计：

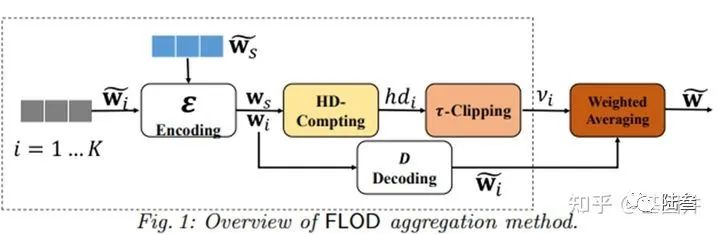
Encoding：

这里是将客户端的上传的梯度更新  和服务器自己训练出来的  先使用SignSGD进行了量化，然后再进一步编码映射到    上，一方面是便于后面计算汉明距离  ，另一方面是为了后面为整个方案使用密码学工具做铺垫，具体映射方法如下：

e.g. 原始的梯度值为：   客户端本地先将其取符号为：   ,然后再经过Enconding变为：  。

需要特别说明的是这里是将   中的    变为   ，  中的    变为  ，主要是为了再后面 Deconding 时使用减法操作，如果之间把   中的    变为  ，就需要进行判断操作，这一操作在后续应用了密码学工具的框架中相比于减法操作是昂贵的。

HD-Computing：

对上述Encoding的结果分别与服务器端梯度更新的结果运算来计算两者的汉明距离，具体如下：

得到的结果就是汉明距离，后面会以汉明距离为基础来判定数据是否异常，那么为什么汉明距离能够其作用呢？文中也给出了证明如下：对于已经使用SignSGD的梯度向量  和  )使用Eqn(1),Eqn(2)得计算向量之间的余弦距离得：

证明表明，余弦距离和本文使用得汉明距离是具有线性关系得，因此可以使用汉明距离直接替换汉明距离。

  -Clipping:

这一步就类似于 FLTrust 中的 Relu() 函数那一步骤，也就是根据超参    来将汉明距离转化为后面对梯度参数加权平均的参数，具体如下：

也就是如果汉明距离大于等于    则权重值赋为0，否则赋予一个相应的非零值。这样再后面的加权平均中，如果属于汉明距离大的则通过与权重相乘就被剔除掉，也就是Oblivious Defender。

Weight Average：

这一步就很简单了，就是将客户端的数据乘上   -Clipping 中得到的权重然后进行求和取平均即可。具体如下：

随后用结果更行自己的模型参数，并将结果发送给每个客户端即可。

至此，我们已经了解了整体的FLOD模型框架，但是已依然还没有添加密码学工具来保护数据隐私，下面就来介绍如何将密码学工具应用到FLOD框架中。本文的方法呢就是将FLOD部署再两方的服务器  上，并假设两方服务器是半诚实的。其中  保有服务器端的Root Dataset和模型，因此  也就完全拥有了服务器的参考梯度更新向量。接下来先了解整体框架：

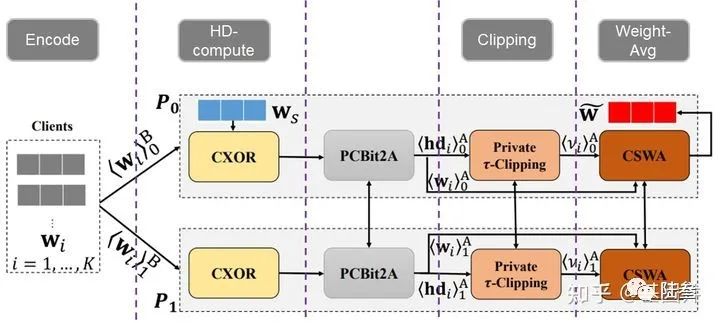
依然先是Encode编码为  上的比特串，这一步和总体框架的过程相同，这里就不再次赘述，编码后的结果客户端用Boolean sharing的方式将结果发送给两个服务器，接下来就是服务器进行的求汉明距离的操作：

Correlated XOR (CXOR)：

这一步的就是在不泄露用户梯度数据的情况下计算原始梯度更新与服务器参考的梯度更新之的汉明距离，并将结果依旧用Boolean sharing的方式保存再两方服务器上，具体方法如下：

  拥有  ，同时  拥有  ，所以两方都可以再本地分别计算   和   。同时可以看到的是  与  依然是  的一个Boolean sharing。所以如此一来本步骤的计算就已经完成。

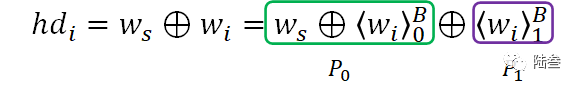
Partial Correlated Bit to Arithmetic Conversion (PCBit2A) ：

因为后面   和CSWA 都需要进行加法、乘法操作。而再目前我们的数据持有方式是布尔分享的，而再此分享上做加法和乘法操作相比较算数分享是昂贵的，因此为了减少通信和计算开销，就需要将布尔分享转化为算法分享，然后再进行后续计算。此步骤就是进行此操作。具体功能如下：

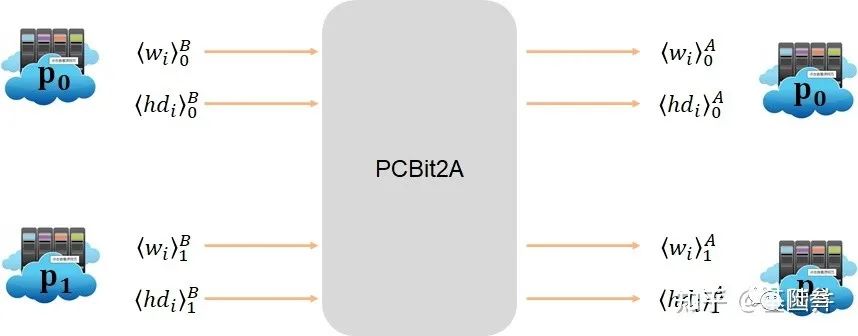
在实现方面，使用了部分元组的方法来进行的，如下图：

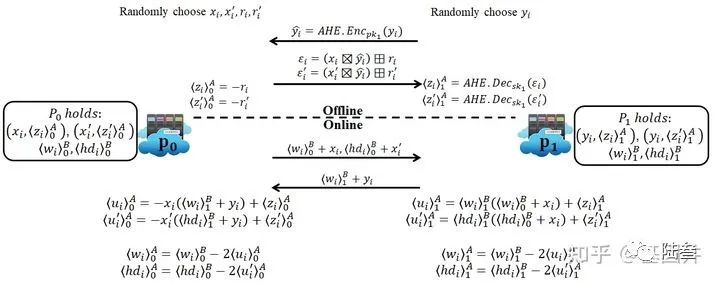
图中  因为在  端  ，所以可以令  ，从而进一步减小通信开销。

Private  -Clipping:

此步骤和最开始一样，进行裁剪，对于汉明距离超过    的，权重赋值为零，其他的则分别赋值一些非零值。以便在最后的加权平均的时候进行剔除。方案如下：

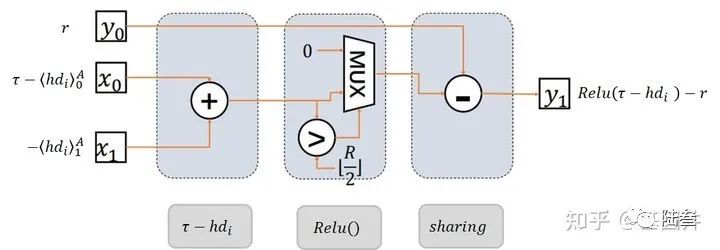
此过程运行过后,    分别持有某一个更新梯度向量的一个算术秘密分享值，其中  持有权重  ，  持有权重   。

Correlated Secure Weighted Aggregation(CSWA)：

该模块功能很简单，就是根据前面得到的梯度更新参数向量以及private  -Clipping得到的对应权重进行加权求和即可：

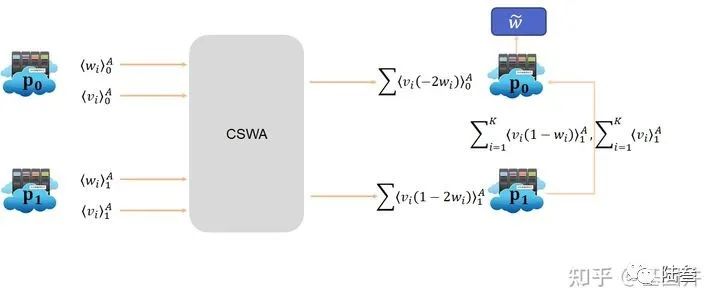
需要特别说明的是，最终的聚合结果将由  完成，因为   需要用结果梯度去更新自己的维护的服务器端的模型，以和各客户端保持一致。具体算法流程如下：

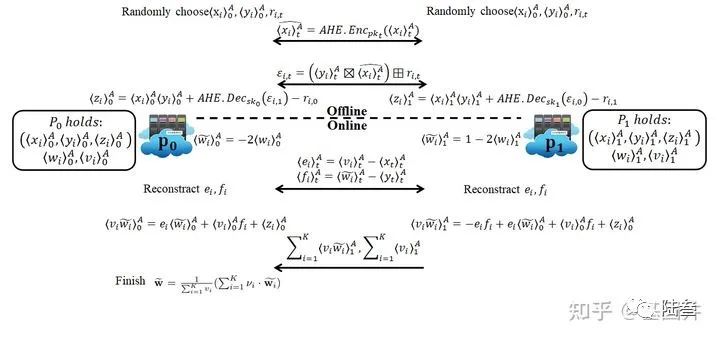
离线阶段是生成   的算数分享三元组，以用来后续进行乘法计算。相比于普通的Beaver 三元组的方法求乘法，该方案的一个改进就是复用  ，从而使得通信和计算效率的提升。

Evaluations

首先是在MNIST和CIFAR10数据集上对无恶意用户场景下与FedAvg、SIGNSGD的比较，可以看出本文的方法在该情境下的精确度表现非常好，和FedAvg相比仅有很小的差距。

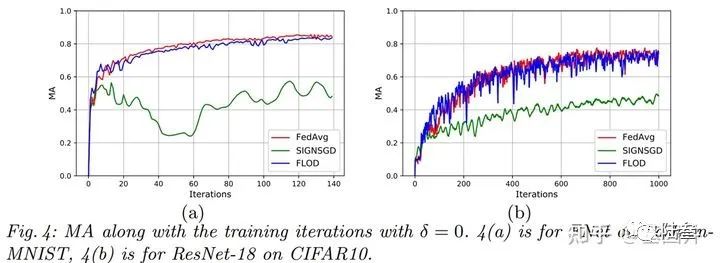
接下来是在不用恶意用户比率下与现有的一些方法作比较,其中(a)图是在高斯攻击下的实验，(b)图是在标签反转攻击下的实验。可以看出，本文的方案是非常有效的，并且很明显的看出本文的方法是可以解决恶意大多数下的拜占庭将军问题。

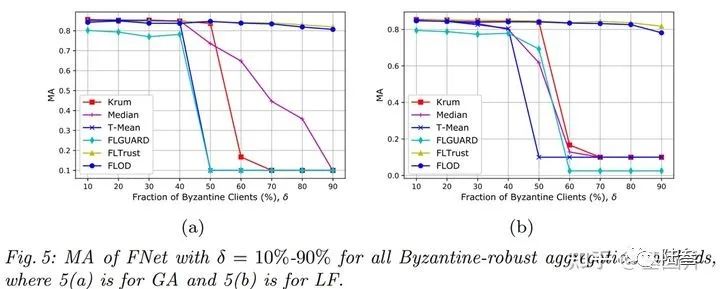
接下来就就需要考虑方案的计算复杂性和通信复杂性，因为隐私保护的很多方案不能够被使用的原因就在于高昂的通信和计算消耗，所以衡量方案的通信和计算消耗很有必要：

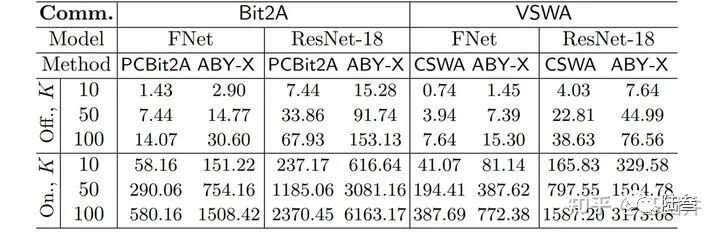
首先是PCBit2A 与 ABY-AHE中的B2A 和 CSWA 与 ABY-AHE中的乘法在通信复杂度上作比较，可以看出无论是在线还是离线状态，都有2倍或以上的提升。而且计算消耗具有同样的情况，具体可以看原文实验。

Summary

拜占庭鲁棒性：

提出一个基于汉明距离的联邦学习算法，该方案可以在恶意大多数场景下解决拜占庭鲁棒性问题。

隐私保护：

在半诚实假设下，在设计了在两方上使用 FLOD 方案来完成聚合过程，从而保护用户数据隐私。

实验性能：

1、在很小的精度损失和收敛速率损失下能够抵抗所有现有的拜占庭攻击.

2、相比于ABY-AHE方法，该方法在 B2A 转化上离线阶段性能提升2倍以上。

3、相比于FLGUARD算法，总体的在线运行时间和通信时间分别提升3.1倍和167倍以上。

参考文献

[1] Bernstein J, Wang Y X, Azizzadenesheli K, et al. signSGD: Compressed optimisation for non-convex problems[C]//International Conference on Machine Learning. PMLR, 2018: 560-569.

[2] Cao X, Fang M, Liu J, et al. FLTrust: Byzantine-robust Federated Learning via Trust Bootstrapping[J]. arXiv preprint arXiv:2012.13995, 2020.

[3] Nguyen T D, Rieger P, Yalame H, et al. FLGUARD: Secure and Private Federated Learning[J]. arXiv preprint arXiv:2101.02281, 2021.

[4] Demmler D, Schneider T, Zohner M. ABY-A framework for efficient mixed-protocol secure two-party computation[C]//NDSS. 2015.

[5] agdasaryan, E., Veit, A., Hua, Y., Estrin, D., Shmatikov, V.: How to backdoor federated learning. In: International Conference on Artificial Intelligence and Statistics. pp. 2938–2948. PMLR (2020)

[6] Bookstein, A., Kulyukin, V.A., Raita, T.: Generalized hamming distance. Information Retrieval 5(4), 353–375 (2002)

往期内容：

满足差分隐私约束的深度学习系统详解

全同态加密框架

差分隐私的定义、直观理解与基本性质

MPC协议之简图

FALCON: 面向诚实大多数场景的恶意安全深度学习框架

论文笔记：IJCAI 2021 Decentralized Federated Graph Neural Networks

欢迎投稿

邮箱：kedakeyin@163.com

参与更多讨论，请添加小编微信加入交流群