作者简介:
冯浩哲, 浙江大学计算机学院,CAD&CG国家重点实验室三年级博士生,导师陈为教授。主要研究方向为迁移学习,无监督表征学习,以及隐私保护的模型训练。以第一作者身份在AAAI/ICML/TKDE上发表多篇论文。知乎:捡到一束光
在文章《差分隐私的定义、直观理解与基本性质》中,我们简单介绍了欧盟隐私保护条例,即个人对数据具有知情权,拒绝权,修正与遗忘权,以及对于自动决策过程的选择权。差分隐私对于数据分析过程提出了严格的隐私保护定义,即对于数据库数据的任何分析,以及根据分析结果与其他信息进行的进一步的合并加工,都不会泄露个人隐私。通俗而言,就是对于任何数据分析员,要求分析员在对数据库进行分析后,对数据库中每一个个体的了解不会超过其在分析开始之前的了解。差分隐私的基本原理是控制单个数据对于整个分析结果的影响,对于简单的数据处理过程(如计算平均工资,统计性别比例),通过在数据分析结果中增加高斯噪声,可以令数据分析的机制满足差分隐私的约束。但是,对于需要多轮训练的复杂深度学习系统,构建差分隐私保护则更为困难。本文主要介绍基于高斯机制的差分隐私深度学习系统:通过在训练过程中施加高斯噪声,构建满足差分隐私要求的深度学习训练系统,并对所得深度模型计算隐私开销。此外,我们也将以Opacus这一基于pytorch的差分隐私训练库为例进行代码讲解。
本文主要参考的文献为
A Tutorial to Differentially Private Machine Learning, Neurips17
Deep learning with differential privacy
Rényi differential privacy
Subsampled Rényi Differential Privacy and Analytical Moments Accountant
Rényi Differential Privacy of the Sampled Gaussian Mechanism
The Composition Theorem for Differential Privacy
Introducing Opacus: A high-speed library for training PyTorch models with differential privacy
A general approach to adding differential privacy to iterative training procedures
差分隐私深度学习系统的基本框架
深度学习的训练与推断流程通常由四步组成:构建深度模型并初始化模型参数;输入训练数据并计算梯度;用梯度下降法更新模型直到收敛;将收敛的模型用于数据预测。最直接的隐私保护方法是对模型预测直接添加噪声,由于深度学习的模型参数非常容易获取,因此仅仅在预测阶段添加噪声往往无法达到隐私保护的目的。利用差分隐私的传递性特征,即对于满足
首先,我们定义深度学习系统中的差分隐私如下:
(Definition 1. Differential Privacy in Deep Training System) 记数据集为
在该定义下,数据集中的单个数据对于模型的影响被控制在一定的范围内,实现了在模型层面对于差分攻击的“不可分辨性”。此外,为了叙述方便,我们提前引入差分隐私的一个变种——Rényi Differential Privacy (RDP)。我们将在计算隐私开销时体会到RDP的威力。
(Definition 2. Rényi Differential Privacy in DL-system) 对于Definition 1中所述的训练机制
(Proposition 1. From RDP to DP) RDP和DP可以进行直接转换,如果训练机制
在深度学习的训练中,模型参数采用梯度下降法进行更新,即
其中
(Definition 3. Gaussian Mechanism) 假设存在一个确定函数
利用高斯机制,我们对梯度分三个步骤增加差分噪声:首先,对每一个样本对应的梯度裁剪到一个固定范围
然后,对裁剪后的梯度增加高斯噪声
完整算法如下图所述:

模型一共进行了
Subsample:用采样率对隐私进行Amplify,降低差分隐私损失
在深度学习的训练过程中,由于数据量比较大,我们往往采用基于随机采样的梯度下降法,即每次选取一个Batch,在该Batch上计算平均梯度,采用它们的平均梯度进行梯度下降。那么,这种基于采样的方法对隐私损失会有什么样的影响呢?我们先不加证明地给出一个结论,即采样会增强隐私保护的力度,降低隐私损失。首先对Subsample给出如下的定义:
(Definition 4. Subsample) 给定一个含有
考虑先对数据集
当


在这些Bound中,某些情况下
Composition Theorem:计算整个训练系统的差分隐私损失
深度学习系统在经过一轮由Subsample,梯度计算,梯度裁剪,高斯加噪组成的训练后,得到了一组满足
一般而言我们取
对于
因此,我们对
简写为
因此,训练系统
那么,如何利用隐私随机变量  的一阶矩(
的一阶矩(
此外,利用
因为差分隐私界需要遍历所有的相邻数据集
利用最大值的性质,我们有
因此,
(Proposition 2 Moments Accountant and RDP) 对于任意的  时刻具有随机性的训练机制
时刻具有随机性的训练机制
(Proposition 3 From Moments Accountant to
在
给定
给定
利用Proposition 3,我们可以从概率角度对差分隐私进行新的理解:给定相邻数据集
也就是说,此时
在上文中,我们讨论了整个训练系统的差分隐私损失计算,并介绍了Moments Accountant这一具备很多良好性质的武器。但是,
(Proposition 4. Calculations of Moments Accountant with Gaussian Mechanism) 考虑具有随机Subsample的高斯机制,其中高斯机制的噪声乘子(noise multiplier)为方差
注意到此时
此时,对于任意正整数
将其代入则可得到
此外,文献[2]还给了一个近似上界,即
综上所述,对于一个使用高斯机制的深度学习训练系统,计算隐私损失大概可以分为三步(这也是Tensorflow的Moments Accountant官方库中的计算方法):
确定给定的噪声乘子
对某个范围的
确定
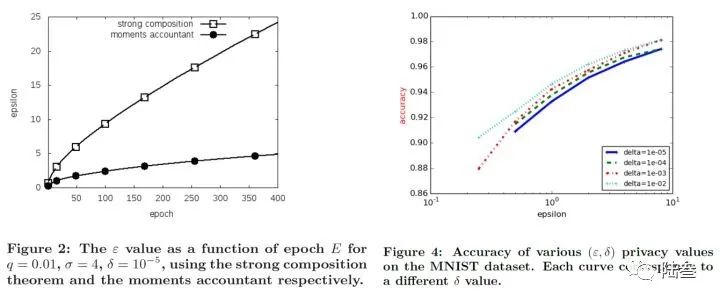
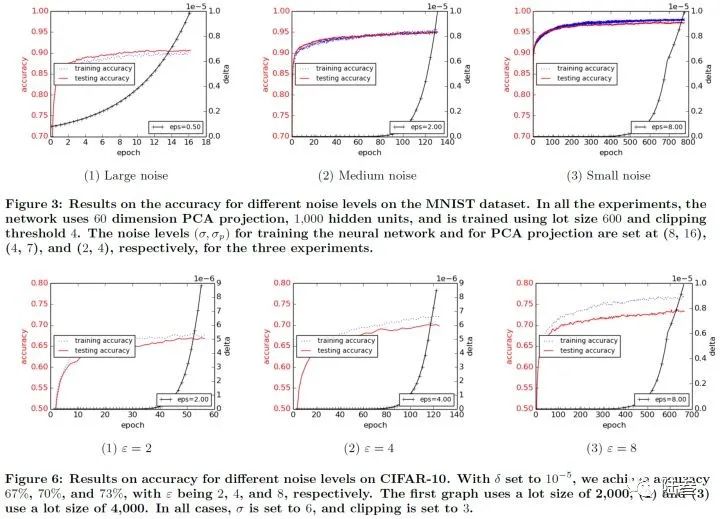
文献[2]在MNIST和Cifar上都进行了实验,比较基于Moments Accountant的方法与Strong Composition定理在隐私界上的扩展,以及各个参数对模型性能的影响,如下所述:
Opacus库:基于Pytorch框架的隐私保护库
Opacus是一个高性能,高速的用于训练具有差分隐私的PyTorch模型的函数库。Opacus库提供了主要类函数PrivacyEngine
,作用于Pytorch中提供的优化器optimizer
上,主要代码如下所示:
model = Net()
optimizer = torch.optim.SGD(model.parameters(), lr=0.05)
privacy_engine = PrivacyEngine(
model,
batch_size=32,
sample_size=len(train_loader.dataset),
sample_rate = 0.01,
alphas=range(2,32),
noise_multiplier=1.3,
max_grad_norm=1.0,
)
privacy_engine.attach(optimizer)
其中,PrivacyEngine
以torch.Module
作为模型输入,alpha
是RDP中所使用的 noise_multiplier
是高斯机制中的 max_grad_norm
是梯度裁剪范围 sample_size
确定了数据总量 batch size
与sample_rate
用于计算采样率 batch_size
大小的数据,在上面计算梯度,最后将多个batch
汇总成一个Lots
进行梯度加噪与参数更新,即L = sample_size*sample_rate
,此时q=sample_rate
。注意sample rate
是一个可选参数,如果不给定sample rate
,那么模型就会令Lots=batch_size
,此时模型每次计算完一个Batch就进行梯度更新。
此外,为了计算隐私开销,Opacus提供了get_privacy_spent
函数,它在给定
epsilon, best_alpha = optimizer.privacy_engine.get_privacy_spent(delta)
训练过程主要采用高斯噪声对梯度进行加噪,噪声方差为
def _generate_noise(
engine, max_grad_norm: float, grad: torch.Tensor
) -> torch.Tensor:
if engine.noise_multiplier > 0 and max_grad_norm > 0:
return torch.normal(
0,
engine.noise_multiplier * max_grad_norm,
grad.shape,
device=engine.device,
generator=engine.random_number_generator,
)
return torch.zeros(grad.shape, device=engine.device)
训练过程中的Subsample与MiniBatch
在DP-SGD的实现算法中,模型参数更新以Lots
为单位,即在所有的训练集中按比率 Lots
,然后对于Lots
中的每个样本计算梯度,然后汇总梯度依次进行gradient clip
、noise adding
以及SGD
。但是,在常见训练过程中,我们往往以batch
为单位计算梯度并进行模型更新。虽然我们确实可以将Lots
的大小设置为与batch size
等同,此时q
无限趋向于0(当然这其实也没有什么大问题,也是一个常见的设置),但是在某些场景下,q
并不是越小越好。比如,提前依据下文中公式 Lots
所增加的噪声方差都会很大,因此我们往往会将Lots
的大小设置为batch size
的若干倍。为了在这种场景下进行更新,Opacus
引进了virtual_step
函数,它只会对当前batch
的梯度进行gradient clip
,并将裁剪后的梯度向量放入一个容器,在汇总k个batch
后,对于整个Lots
的数据再调用step
函数进行更新,它将存储在容器中的梯度依据k*batch_size
计算平均值并调用SGD
。基本代码如下所示:
Example:
Imagine you want to train a model with batch size of 2048, but you can only
fit batch size of 128 in your GPU. Then, you can do the following:
>>> for i, (X, y) in enumerate(dataloader):
>>> logits = model(X)
>>> loss = criterion(logits, y)
>>> loss.backward()
>>> if i % 16 == 15:
>>> # accumulate the gradients of a lot and perform SGD.
>>> optimizer.step()
>>> optimizer.zero_grad()
>>> else:
>>> # store the gradients into a gradient accumulator
>>> optimizer.virtual_step() # this will call privacy engine's virtual_step()
对模型参数进行分组裁剪与加噪
差分隐私模块需要对计算后的参数梯度进行裁剪并增加高斯噪声。但是,深度模型的参数所提取的特征与层数有关,不同层对应不同尺度的特征,也对应不同尺度的梯度和方差(如深度卷积网络的浅层提取纹理特征,深层提取语义特征)。因此,对于参数进行分组,对每一个组的梯度单独采用一组
首先,我们将模型参数 Lots
的L个训练数据,我们记第
我们说该过程满足
此外,我们可以将
此时要求
利用梯度函数的性质
我们可以先将输入的向量进行放缩为
由于后处理不改变差分隐私界,因此
将噪声乘子  看成是各层隐私噪声乘子
看成是各层隐私噪声乘子 的一个二次调和平均数。
的一个二次调和平均数。
在Opacus中,通过对原有的nn.optimizer.step
函数进行加噪实现差分隐私,对应的代码实现如下:
def step(self, is_empty: bool = False):
"""
Takes a step for the privacy engine.
Args:
is_empty: Whether the step is taken on an empty batch
In this case, we do not call clip_and_accumulate since there are no per sample gradients.
Notes:
You should not call this method directly. Rather, by attaching your
``PrivacyEngine`` to the optimizer, the ``PrivacyEngine`` would have
the optimizer call this method for you.
"""
self.steps += 1
params = (p for p in self.module.parameters() if p.requires_grad)
for p, clip_value in zip(params, clip_values):
if self.rank == 0:
# 噪声只添加一次,并由第一个线程添加
noise = self._generate_noise(clip_value, p.grad)
# 如果用均值损失,那么噪声也要对应除以均值
if self.loss_reduction == "mean":
noise /= batch_size
p.grad += noise
此外,在Tensorflow中,通过采用NestedQuery
类,可以实现分组的加噪与隐私计算。
超参数选择与采样策略
(超参数选择) 对于一个差分隐私训练过程,如何选取合适的
使用一个先验的全局尺度
统计数据集中对每一个梯度向量的大小,从小到大选取
采用超参数选择法,微调
(采样策略) 在初始的DP-SGD算法中,要求Lots
的选取是i.i.d的,在这种分布下,训练过程可以通过Moments Accountant
计算隐私损失。这种采样策略可以通过无放回采样从训练集中采样一个固定大小的子集完成。但是,在实际使用的过程中,Lots
往往由若干个Batch
组成,而各个Batch
大小相同,彼此没有交集,本质上是一种随机划分。在这种场景下,我们往往也沿用Moments Accountant
的隐私计算,但是Moments Accountant
并不是该采样策略的确界,而关于确界的研究仍然未知。
PySyft + Opacus:结合差分隐私与联邦学习
PySyft
是国际隐私保护开源社区OpenMined所构建的基于联邦学习的多方加密计算方法。联邦学习是一种隐私保护的分布式机器学习流程,它允许多个本地客户端在一个中央服务器的调度下,在多个分布式存储的数据库上训练全局模型,同时保持数据的本地化。联邦学习一般由两个步骤组成,本地模型的训练与中央服务器的聚合。本地模型经过若干个Epoch
的训练,上传模型的更新参数,然后中央服务器对来自各个客户端的参数更新采用多方安全计算(Secure Multi-Party Computation, MPC)进行同态加密(Homomorphic Encryption),在加密后的数据上进行联邦平均(Federated Average),得到全局模型,再将参数发还给本地。联邦学习可以确保用户的数据不出域,但是不能保证模型本身不泄露用户信息。因此,在分布式训练中采用联邦学习,然后在本地训练中采用差分隐私,可以令训练系统达到更高级别的隐私保护。
PySyft
就是利用这一思想,在本地计算时,对模型的训练过程采用DP-SGD算法加入差分隐私机制,然后在联邦学习过程采用多方安全计算,通过联邦平均得到全局模型。这种思想非常简单,几乎可以自己实现(注:在科研论文中,我们往往直接进行联邦平均而不考虑安全性,对于加法与乘法同态的MPC已经是成熟的技术,因此仅在工程中添加)。PySyft
给出了一个简单的代码实现:
# 本地模型添加差分隐私
models, dataloaders, optimizers, privacy_engines = [], [], [], []
for worker in workers:
model = make_model()
optimizer = th.optim.SGD(model.parameters(), lr=0.1)
model.send(worker)
dataset = train_datasets[worker.id]
dataloader = th.utils.data.DataLoader(dataset, batch_size=128, shuffle=True, drop_last=True)
privacy_engine = PrivacyEngine(model,
batch_size=128,
sample_size=len(dataset),
alphas=range(2,32),
noise_multiplier=1.2,
max_grad_norm=1.0)
privacy_engine.attach(optimizer)
models.append(model)
dataloaders.append(dataloader)
optimizers.append(optimizer)
privacy_engines.append(privacy_engine)
# 联邦学习
def send_new_models(local_model, models):
with th.no_grad():
for remote_model in models:
for new_param, remote_param in zip(local_model.parameters(), remote_model.parameters()):
worker = remote_param.location
remote_value = new_param.send(worker)
remote_param.set_(remote_value)
def federated_aggregation(local_model, models):
with th.no_grad():
for local_param, *remote_params in zip(*([local_model.parameters()] + [model.parameters() for model in models])):
param_stack = th.zeros(*remote_params[0].shape)
for remote_param in remote_params:
param_stack += remote_param.copy().get()
param_stack /= len(remote_params)
local_param.set_(param_stack)
我们能做的开放性问题
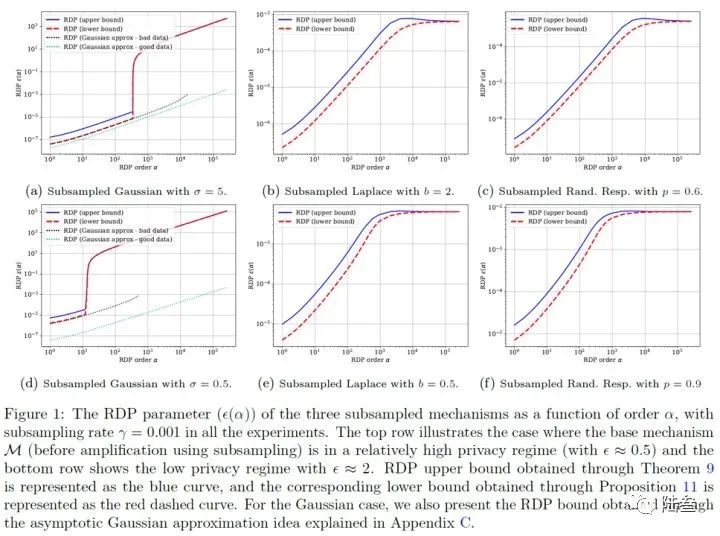
在本节中,我们主要介绍了以高斯机制作为噪声来源,以Moments Accountant作为隐私损失估计的差分隐私深度学习训练系统。但是,这套方法所给出的隐私损失与具体的数据集或是模型都无关,可以看作是任意数据集与任意模型上的一个隐私损失上界。而在实际的应用场景中,考虑特定的数据与特定的模型,我们往往可以设计隐私损失更小的训练方法。文献[4]为基于RDP的差分隐私损失设计了一个上界和一个下界,并巧妙设计了两个数据集场景:
Bad Case,在这种场景中,总是存在两个相邻数据集
, 因此当
Good Case,在这种场景中,前一半数据的查询结果总是
在这两种场景中,Bad Case的RDP总是接近Lowerbound,而Good Case的RDP则比上界要低很多很多,这告诉我们,对于具体的数据集,它的实际隐私损失要大大小于计算出的上界。因此,如何做modle specific,data specific的隐私保护是一个值得研究的问题。实际上,PATE(Private Aggregation of Teacher Ensembles等框架利用一部分有标签数据与大量无标签数据进行半监督学习,在多个模型上进行知识蒸馏,可以大大减小隐私损失。在下一期隐私保护+深度学习的专题研讨中,我们将对这些Data Specific, Model Specific的先进隐私保护方法进行介绍。
Appendix:Rényi 散度的基本性质与RDP的比较优势
(Rényi Divergence). 给定两个满足离散分布的随机变量
其中
扩展到两个离散分布
对于Rényi散度已经有很多研究,推荐阅读Rényi散度与KL散度的关系。Rényi散度有如下几个性质:
对于两个正态分布
定义
定义
注意这条性质的证明实际上有点复杂,需要先用
再利用积分中值定理
代入后就是
定义
RDP的总结与比较优势
RDP是DP的一种自然的推广,当
RDP与DP共享了很多特性,而RDP的计算更加简单,将复杂的遍历计算归结于一个散度计算,这使得RDP可以在实际中使用。
RDP在高斯机制下的计算很简单,结论更加有用。
在相同的隐私损失下,RDP能够添加更小的噪声,使得查询更加准确。
Appendix:Moment Generating Functions
一个随机变量
注意到
因此
如果
矩生成函数一般用于计算多个独立随机变量的和的分布,如果
往期内容:

欢迎投稿
邮箱:kedakeyin@163.com
参与更多讨论,请添加小编微信加入交流群