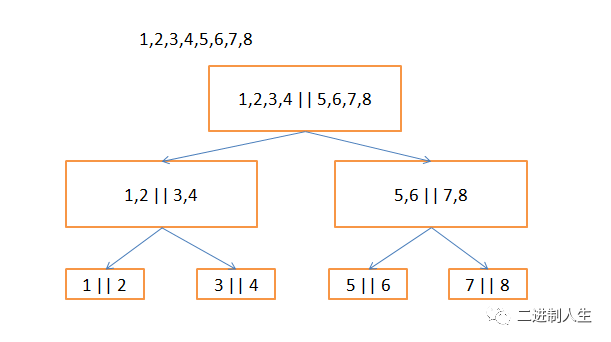
分治:分而治之,把一个复杂的问题分解成很多规模较小的子问题,然后解决这些子问题,把解决的子问题合并起来,大问题就解决了。
二分查找是我们最早接触分治思想的例子,在一个有序数组中查找指定数,暴力的做法就是拿指定数和数组里面每个数比较一下,相同的话就返回下标,这个是大问题。可以把有序顺序以中间数为分水岭分成两部分,待查数比中间数小,说明待查数在前面部分,否则,在后面部分,这样就把一个大问题分解成两个小问题,而每个小问题都可以继续分解,直至找到答案或者不能再分解为止。
条件
当然各个思想都有它的使用领域,所以玩这场分治游戏就要遵守它的游戏规则。
① 求解问题确实能够分解成若干个规模较小的子问题,并且这些子问题最后能够实现接近或者是O(1)时间求解。
② 各个子问题之间不能有依赖关系,并且这些子问题确实能够通过组合得到整个问题的解。
步骤
通过上面对分治的说明,可以看到分治分三步走:
① 分解: 将问题分解成若干了小问题。
② 求解: O(1)的时间解决该子问题。
③ 合并: 子问题逐一合并构成整个问题的解。
我们来看看运用分分治思想解决的几个经典问题。
Top1--第K问题
输入一个无序数组,找到第K小的数。
这就是经典的第K问题,或者说是Topk问题,比如在1000个考生中找分数排名前K的人。
解题思路:
在本质上和快速排序一样,在数组中随便取一个数作为基准base,一般取第一个数,调整数组,将比base小的数放在base的左边,比base大的数放在base的右边,最后记录base的新下标mid(从0开始)。
如果mid刚好等于k-1,那就达到我们的目的了,因为它就是第k小元素。
一般不会那么巧,但是无形中我们已经把这个问题拆解成了两个小问题。如果mid<k,说明第k小元素就在右边那一拨,相反,则在左边那一拨。
那就继续采取同样的办法将这一拨数据重新分成两拨,直到mid=k为止。如果这样一直分下去直到最后一拨的数据只剩一个,那这就是快速排序了。
#include <sys/time.h>
#include <stdio.h>
#define N 20
void getData(int d[], int n)
{
time_t t;
srand((unsigned) time(&t)); /* 设置随机数起始值 */
int i;
for(i=0; i < n; i++)
d[i] = rand() % 100; /* 获得0-99之间的整数值 */
}
void result_output(int a[])
{
int i;
for (i = 0; i < N; i++)
printf("%d ", a[i]);
printf("\n");
}
int split(int a[], int low, int high)
{
int part_element = a[low];
for (;;) {
while (low < high && part_element <= a[high])
high--;
if (low >= high) break;
a[low++] = a[high];
while (low < high && a[low] <= part_element)
low++;
if (low >= high) break;
a[high--] = a[low];
}
a[low] = part_element;
return high;
}
int select(int a[], int low, int high, int k)
{
int middle;
for(;;) {
middle = split(a, low, high);
if(middle == k)
return a[k];
else if(middle < k)
low = middle+1;
else /* if(middle > k) */
high = middle-1;
}
}
int main(void)
{
int a[N], k, r;
getData(a, N); /* 获得数据放入数组a中 */
printf("datas: \n");
result_output(a);
scanf("%d", &k);
if(k >= 0 && k <= N-1) {
r = select(a, 0, N - 1, k-1);
printf("result=%d\n", r);
} else
printf("input error: k=%d\n", k);
return 0;
}
Top2—归并排序
归并排序是分治法的一个典型的应用。先使每个子序列有序,再将两个有序子序列合并成一个有序表。
如图所示就是归并排序的基本步骤。首先利用函数递归,将原数组不断分割直至变成不可分割的,只含一个元素的子序列,此时每个子序列都能被看成是有序的子序列。然后进行合并,每一轮合并将逆着拆分的过程逐渐在原数组中形成有序。下面这张图很形象的描述了归并排序的过程。
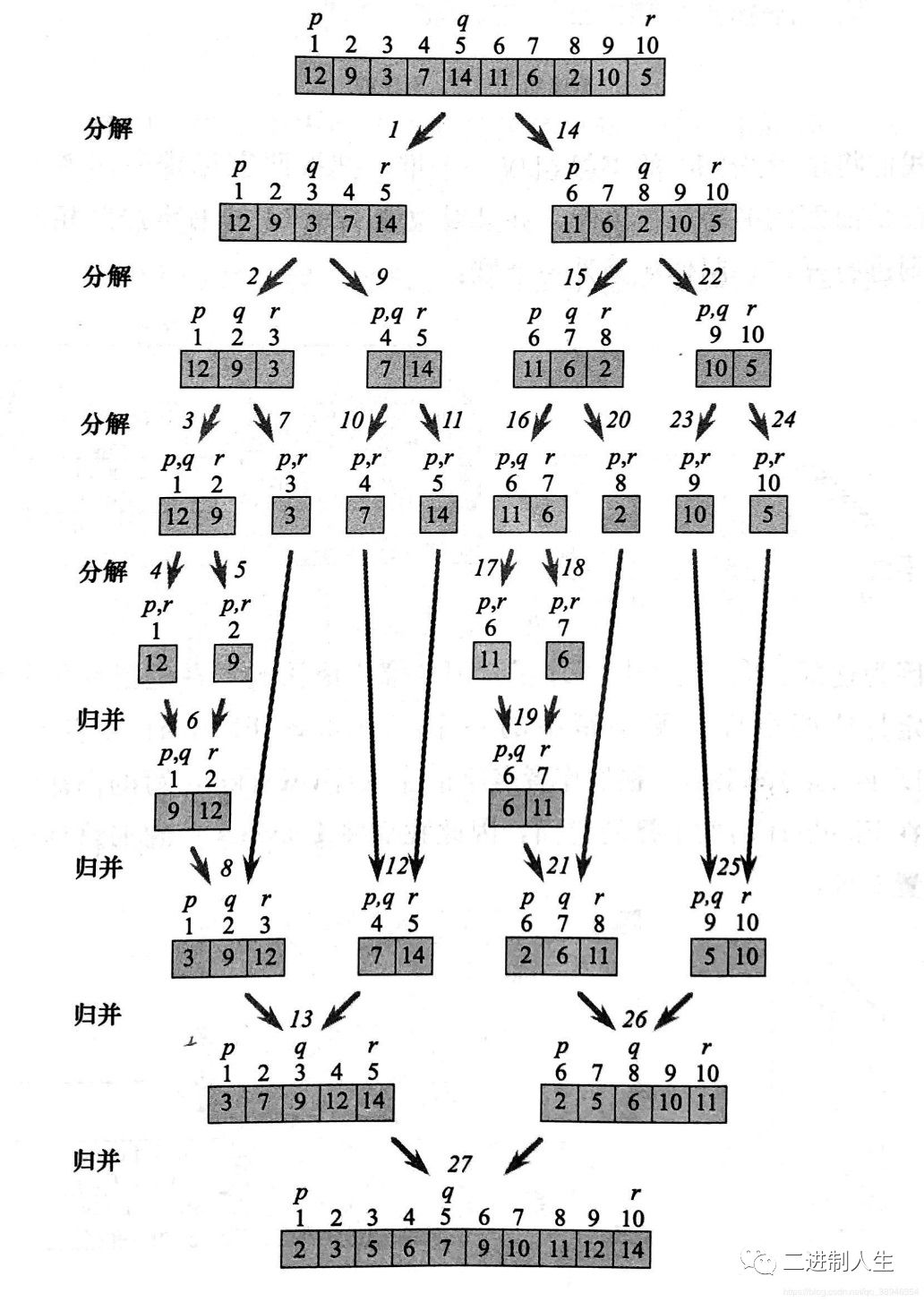
复杂度:
平均、最好、最坏的时间复杂度都为:O(n*log n)。在数据量较大时,归并排序是一种效率很高的方法,使用时需要注意内存空间利用的问题,因为递归次数太多容易造成爆栈;在数据量较小比如数组中只有50个元素要排序时,其速度甚至低于冒泡排序。
void MergeArray(int a[], int start, int mid, int end, int temp[]){
int i = start, j = mid + 1, k = 0;
while(i <= mid && j <= end){ //合并两个数组时,将两个数组的元素逐个比较,
较小的放在临时数组的前面形成有序,一个数组复制结束后就退出if(a[i] < a[j]) temp[k++] = a[i++];
else temp[k++] = a[j++];
}
while(i <= mid){ //若此时左端数组未复制完,就将左端数组未复制完的部分直接连
在临时数组后面temp[k++] = a[i++];
}
while(j <= end){ //若此时右端数组未复制完,
就将右端数组未复制完的部分直接连在临时数组后面temp[k++] = a[j++];
}
for(i = 0; i < k; i++){ //将临时数组中已排序的好的元素复制到原数组对应位置
a[start + i] = temp[i];
}
}
void MergeSort(int a[], int start, int end, int temp[]){
if(start >= end) return; //只有一个元素了,不用再分解
int mid = (start + end) / 2;
MergeSort(a, start, mid, temp); //递归拆分
MergeSort(a, mid+1, end, temp); //递归拆分
MergeArray(a, start, mid, end, temp); //合并
}
int main()
{
int a[20] = {5,32,6,4,8,9,23,16,67,13,65,78,12,15,68,45,21,34,54,78};
int b[20];
MergeSort(a,0,19,b);
for(int i=0;i<20;i++)
printf("%d,",b[i]);
}
Top3—快速排序
将第K问题稍作修改,即得到快排。
void split(int a[], int low, int high)
{
int base = a[low];
int tmp = high;
for (;;) {
while (low < high && base <= a[high])
high--;
if (low >= high) break;
a[low++] = a[high];
while (low < high && a[low] < base)
low++;
if (low >= high) break;
a[high--] = a[low];
}
a[low] = base;
if(low-1>0)
split(a,0,low-1);
if(low+1<tmp)
split(a,low+1,tmp);
}
我们顺便来分析下快排的复杂度。因为很多人不理解nlogn是怎么来的。实际上,严谨的写法应该是nlog2n,注意2是底数,这里没写成下标。
快速排序的基本思想是:每次从无序的序列中找出一个数作为中间点(可以把第一个数作为中间点),然后把小于中间点的数放在中间点的左边,把大于中间点的数放在中间点的右边;对以上过程重复log(n)次得到有序的序列。
快速排序的时间复杂性分析:排序的大体如下图所示,假设有1到8代表要排序的数,快速排序会递归log(8)=3次,每次对n个数进行一次处理,所以他的时间复杂度为n*log(n)。所以排序问题的时间复杂度可以认为是对排序数据的总的操作次数。