引言:本文是《统计数据会说谎》这本经典之作的总结笔记。英文书名(How to Lie with Statistics)像是要教你如何用统计数据说谎,实则是要帮助你如何戳穿谎言。本文将用大量案例,帮你快速了解本书的精华,学会戳穿统计数字背后的各种谎言。
马克·吐温有一句统计名言:
世界上有三种谎言:谎言、该死的谎言、统计数字。
There are three kinds of lies: lies,damned lies,and statistics.

表达的意思就是:看似客观科学的统计数字背后,其实隐藏着很多陷阱。
比如最近我在网上看到的这样一则新闻:
腾讯财报显示,截至2021年6月30日公司有94,182名员工,期间总酬金成本为人民币443.88亿元,按6个月计算,腾讯员工平均每月工资为7.85万元。(新闻链接:https://www.sohu.com/a/484315185_120800259)
这里先提出一个思考题:你觉得新闻里的这个7.85万的平均月薪统计得有问题吗?这其中包含了哪些陷阱?
或许读完本文能给你些启发。
一、统计数字有哪些陷阱
1.带有偏差的样本
案例:
某高校调查某年毕业生平均年薪25W。
分析:
这些数据是如何得到的?样本多大?调查样本具有代表性吗?
实际上,愿意参与调查可能只是问卷调查设计人群的20%。还有部分人虚荣心作祟,虚报薪水状况,导致所调查年薪偏高。
其实样本偏差总会存在,只能做到尽量减少偏差。
如果你上街做随机调查,就会因遗漏了宅男宅女而产生偏差;
如果你挨家挨户做上门调查,就会遗漏大多数白天上班的人;
如果你转而改为晚上做上门调查,又会遗漏晚上在电影院和夜总会的人。
2.精挑细选的平均数
“不会游泳的小明身高1.3米,走过平均水深0.8米的小河,有没有危险?”
这个应该都知道,当然会有危险,因为平均水深0.8米的小河,往往最深处可能有2米以上。
平均数的陷阱是存在多种平均数算法:算术平均数、中位数、众数
这几个平均数可能差别很大,如下图所示:
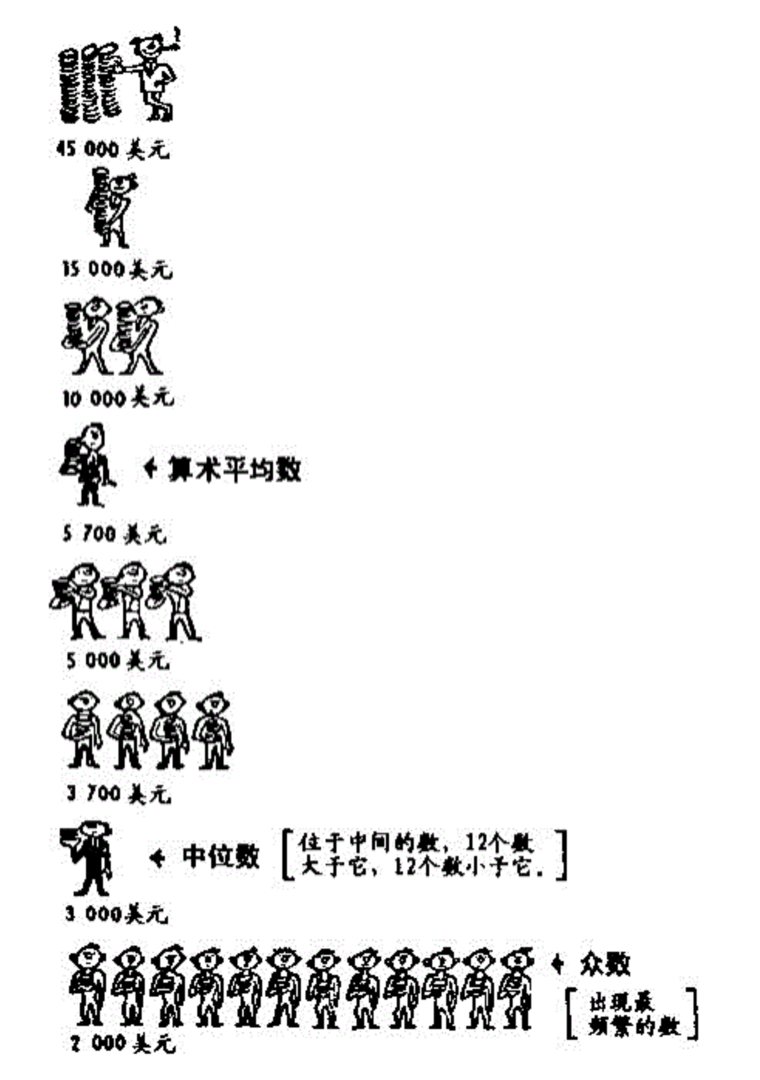
(一个公司的员工薪酬分布)
3.没有透露的小小数
案例1:
某公司开发一款牙膏,宣称治疗蛀牙效果明显,可以使蛀牙减少23%。
分析:
事实上公司采用了12人的实验样本,如此小的实验样本误差肯定偏大,不能反馈真实情况。
案例2:
几年前,有个小儿麻痹症疫苗实验。一个社区中有450名儿童接种了疫苗,680名儿童作为对照组没有接种疫苗。
不久,该区域感染了流行病,接种疫苗的所有儿童都未患上小儿麻痹症,而对照组的儿童也没有患病。这是怎么了?
分析:
忽略了该病的低发生率,这种规模的人群预计只会产生2名以下患者。
实验从一开始便注定是毫无意义。将实验规模扩大到20倍,才能产生足具说服力的结果。
一个更简单的例子,抛了10次硬币,得到8次正面,就能证明正面朝上的概率是80%?
身边案例还有很多,比如会预测足球比赛的章鱼保罗、宣称年化收益50.96%的炒股大师。。。

4.惊人的图形
通过改变图形的坐标轴,可以达到惊人的效果。
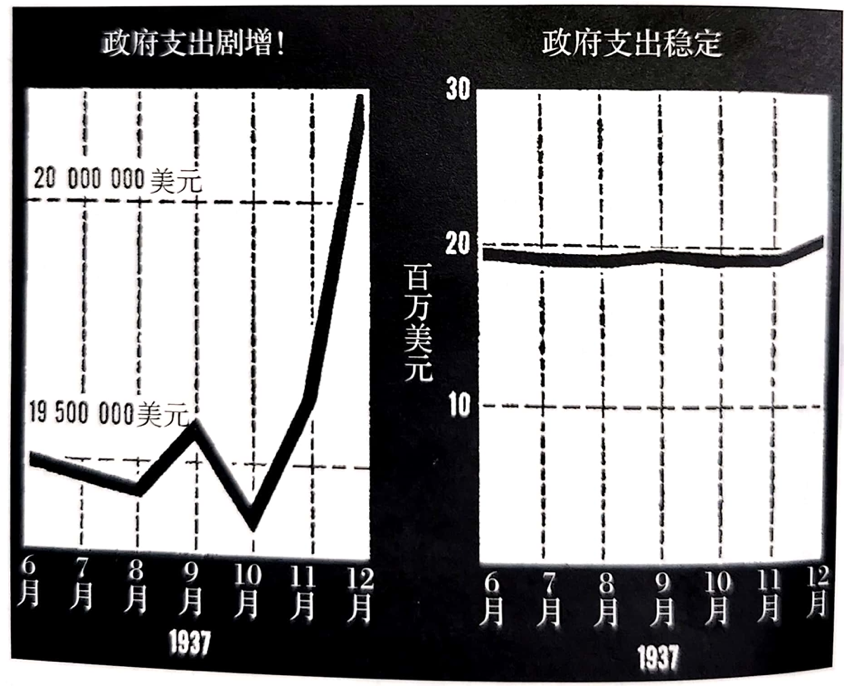
上面两张图都来自同一份数据,1937年美国政府支出趋势:1950万到2000万,增长2.6%
为何左边的看起来增长迅猛,而右边看起来走势平稳?
原因就在于左图的纵坐标不是从0开始,截了一段,就显得增长迅猛了。
5.看似相关的数据
案例:
1898年“美西战争”期间,美国海军的死亡率是9‰,而同期纽约市市民的死亡率为16‰
海军征兵部门的人就拿这个数据来说明待在部队更安全。
分析:
海军的主要构成人员是年轻人。而市民包含了婴儿、老年人、病人等。这些人不管在哪里都是高死亡率的人群。
6.因果颠倒
相关关系≠因果关系
案例:
有篇医学报告得出结论:爱喝牛奶的人更容易得癌症。
新英格兰和瑞士等地的癌症患者人数不断增加,这些地方是牛奶的主要生产和消费区。但是在斯里兰卡得癌症的人却不多,因为在这里牛奶很稀缺。
分析:
癌症主要在中老年人群发生,实际是瑞士等国家的人均寿命相对较长,所以癌症发病人数也更多。
二、如何操纵统计
案例1:平均数的算法
美国普查局调查某年美国家庭的平均收入是3100美元,但是同年有一则新闻中报出的家庭平均收入却为5005美元,为何这两组数字相差如此大?
分析:
新闻中的5005美元用了这样的算法:将美国居民总收入除以总人数,得到人均1251美元,于是一个四口之家的平均总收入为1251*4=5005美元。
这种奇怪的算法在两方面进行了夸张:
1.使用了均值,而非更具代表性的中位数
2.它假设了家庭收入和家庭人口数成正比,实际并非如此
这个案例也说明:对于那些未经解释的平均值,我们根本不用在意!
案例2:为使统计数据看上去更精确,使用小数
询问100个人昨晚的睡眠时间,加总后求均值,得出结论:人们平均每天睡眠7.831小时。这个数字听上去就比平均睡眠8小时左右更加精确。
分析:
这种数据从一开始就不可能很精确,人们不可能精确到分地说出昨晚的睡眠时间,每个样本跟实际相差15分钟都很正常,这种数据使用小数毫无意义。
案例3:基数变换
一个促销商品,先打50%的折扣,再优惠了20%折扣,实际一共打了几折?
分析:
听上去像打了70%的折扣,其实只有60%,因为后面20%的折扣是按五折后的价格计算的。
案例4:将不可直接相加的百分比错误地直接相加
图书价格的上涨主要是由于生成和原材料的成本上升造成的:
加工成本上涨了11%;材料成本上涨了9%;销售及广告上涨了10%。将所有这些加起来总成本只是上涨了30%。
分析:
每项成本都上升10%左右,总成本其实也只会上升10%。
案例5:
假设去年一瓶牛奶10美元,一条面包10美分。
今年牛奶价格降至5美元,而面包价格升至20美分。
问:
物价指数上升了?
物价指数下降了?
还是根本没有变化?
分析:可以通过不同的统计方法得出各种结果
// 想证明物价指数上升:
选择去年为基数,今年牛奶价格降低为50%,面包价格升高为200%。
50%和200%求平均得125%,与去年相比,今年上涨了25%。
// 想证明物价指数下降:
选择今年为基数,去年牛奶价格是今年的200%,而面包价格是今年的50%,求平均得125%,就是说去年比今年上涨了25%,今年价格下降了。
// 想证明物价指数没有变化:
用几何平均数,选择去年为基数,今年牛奶价格降低为50%,面包价格升高为200%,50%乘以200%再开平方根,得100%,价格没有变化。
三、如何揭穿陷阱
1.是谁这么说?
是哪个专家说的?
这专家到底是不是权威人士,还是只和权威沾了点边。
2.他怎么知道的?
调查的样本是否存在偏差?相关性是否显著?
3.漏掉了什么?
平均数和中位数有着本质差别
有没有对比数据
只给出百分数,却没有给出原始数据,是否隐藏了重要信息
4.有人偷换概念了吗?
要注意在原始数据和最终结论之间有没有什么地方被偷换了概念,导致前后数据口径不一致,名词定义混乱。
5.这是否合乎情理?
能让人印象深刻的精确数据可能与常识相悖的。
(如:纽约的一份报纸称,一个职业女性每周至少需要挣够40.13美元才能养家糊口。然而,维持生活的花费不可能精确计算到美分。)
警惕外推法:截至目前的趋势或许是事实,但是未来的趋势不过是预测者的猜测。
(外推法:比如美国股市持续上涨了10多年,未来10年是否会延续上涨真的不一定。)
总结如下图:
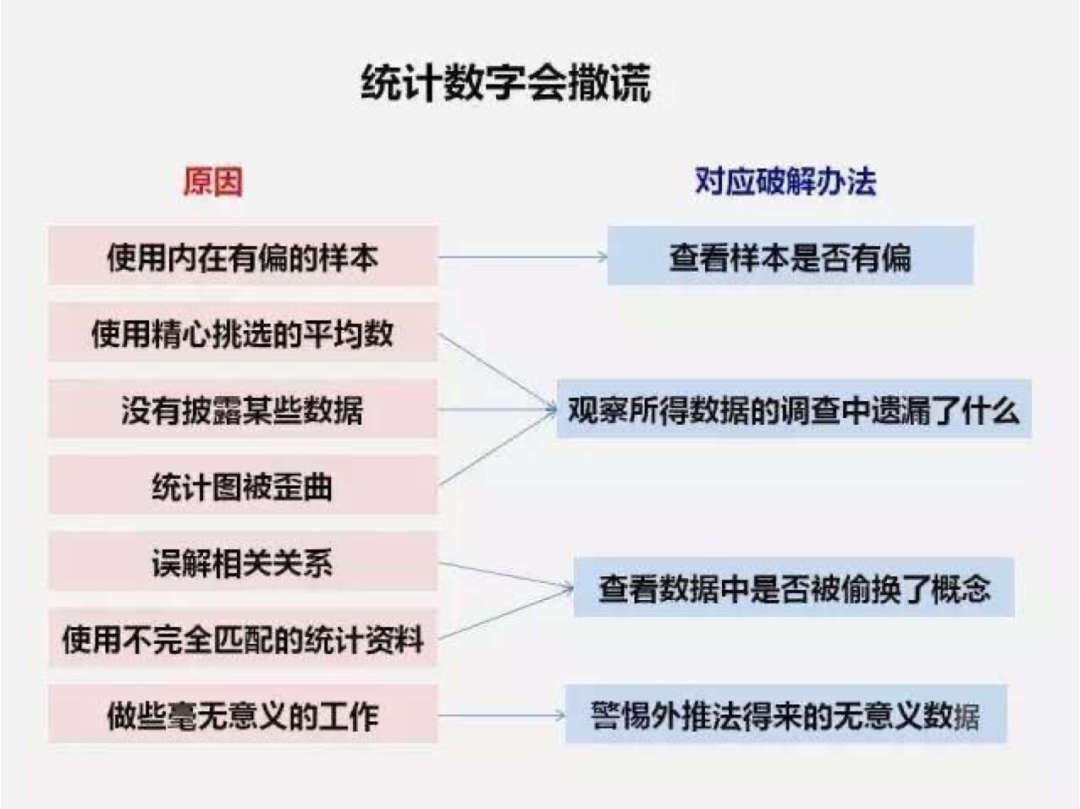
这里,让我们再回到文章开头的那个新闻:

在我看来这里面有2个陷阱:
1.一个是偷换概念
将平均薪酬成本偷换为平均月薪。
财报里给出的薪酬成本,除了工资外,还包含:社保五险一金、餐补、交通补助、差旅费用等其他人工成本。
总薪酬成本除以总人数,明明是平均薪酬成本,偷换概念成平均月薪。
2.另一个是平均数陷阱
这里用了算数平均数而非中位数。
实际上,根据腾讯2020年年报披露,腾讯13位高层(包括执行董事在内)2020年总酬金大约31.64亿元(公司半年总酬金443.88亿元),只这13个高层就占了总薪酬的很大的比例,这样取平均值会产生严重偏差。更准确描述的话应该用中位数。
希望这篇《统计数据会说谎》的总结笔记能给你有所启发~






