上周承诺大家本周会推出一篇逻辑回归项目实战的文章,终于和大家见面啦
 。
。
在Python中如何实现逻辑回归建模
1.1 调用sklearn库
1.2 逻辑回归常用参数详解
逻辑回归建模项目实战
2.1 导入基本库并设置文件存放路径
2.2 导入待建模的数据
2.3 分析数据基本情况
2.4 用IV挑选变量
2.5 建立模型
2.6 把模型转成评分卡的形式
一、在Python中如何实现逻辑回归建模

1 调用sklearn库
from sklearn.linear_model import LogisticRegression as lr
2 逻辑回归常用参数详解
逻辑回归函数中有很多参数,可以根据自己的数据进行相应调整。如果觉得纯看参数解释会有点枯燥,可以先看本文第二部分项目实战,有需要的时候再回过头来看这部分。
LogisticRegression( solver='lbfgs', penalty='l2', class_weight=None, tol=0.0001, random_state=None, C=1.0, fit_intercept=True, intercept_scaling=1, dual=False, max_iter=100, multi_class='auto', verbose=0, warm_start=False, n_jobs=None, l1_ratio=None)
1.liblinear:使用开源的liblinear库实现,内部使用坐标轴下降法来迭代优化损失函数,适用于小数据集。
2.lbfgs:拟牛顿法的一种,利用损失函数二阶导数矩阵(海森矩阵)来迭代优化损失函数。
3.newton-cg:牛顿法家族中的一种,利用损失函数二阶导数矩阵(海森矩阵)来迭代优化损失函数。
4.sag:随机平均梯度下降,是梯度下降法的变种,和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度,适合于样本数据多的时候。
5.saga:线性收敛的随机优化算法的的变种,适用于大数据集。
注1:对于常见的多元逻辑回归(OvR)和(MvM),一般(MvM)比(OvR)分类相对准确一些,但是liblinear只支持(OvR)不支持(MvM)。这意味着我们需要相对精确的多元逻辑回归时,不能选择liblinear,从而也不可以使用优化算法只能选择liblinear的L1正则。
注2:sag每次仅仅使用了部分样本进行梯度迭代,所以当样本量少的时候最好不要选择它。而如果样本量非常大,比如大于10万,sag是第一选择。但是sag不能用于L1正则化(没有连续导数)。如果你有大量的样本,同时模型的特征非常多,想要用L1正则化让模型系数稀疏化,这时就需要进行取舍。要么通过对样本采样来降低样本量 ,要么通过特征筛选提前挑选出重要变量,要么回到L2正则化。
1.样本高度失衡。比如在第三方支付公司的欺诈领域,由于欺诈商户是极少一的部分,绝大部分的商户是正常商户。在建立欺诈模型的时候,99901个商户是正常商户,99个商户是欺诈商户。即0.1%的商户是欺诈商户,99.9%的商户是正常商户。如果我们不考虑权重,把所有商户都预测成正常商户,那么模型的预测准确率为99.9%,但是这种预测结果是没有任何意义的,没有抓到任何欺诈商户  。
。2.误分类代价很高。如果我们将欺诈商户分类为正常商户,可能会带来上万的损失。这时,在模型上我们可能愿意误判一些正常商户,让监控运营进行甄别,尽可能多地识别出欺诈商户,减少资金损失。

想根据这批历史数据训练逻辑回归模型,得到模型参数,预测未来新申请的客户逾期概率。从而决定新申请人是通过、转人工核验还是拒绝。
1 导入基本库并设置文件存放路径
# coding: utf-8import os #导入设置路径的库import pandas as pd #导入数据处理的库import numpy as np #导入数据处理的库os.chdir('F:/微信公众号/Python/19.逻辑回归/项目实战数据') #把路径改为数据存放的路径os.getcwd() #看下当前路径
2 导入待建模的数据
data = pd.read_csv('testtdmodel.csv',sep=',',encoding='gb18030')
UnicodeDecodeError: 'utf-8' codec can't decode byte 0xb6 in position 2: invalid start byte
3.1用head函数看下数据表头和前几行数据
data.head(2)
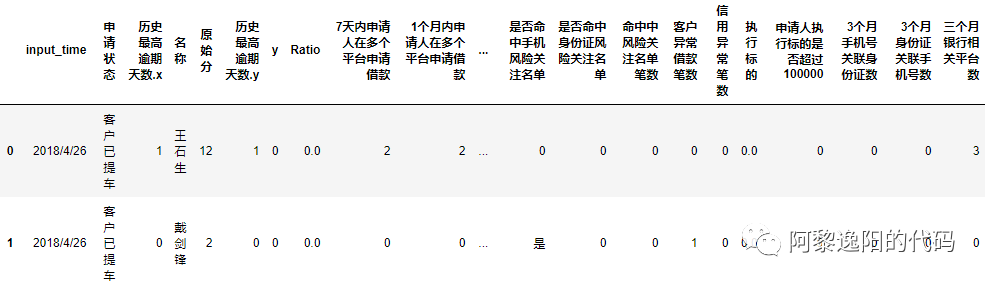
3.2用value_counts函数观测因变量y的数据分布
在信贷中,有些客户因为忘记了还款日期、或者资金在短期内存在缺口(不是恶意不还),可能会导致几天的逾期,在催收后会及时还款。
在本文把逾期超过20天的客户标签y定义为1(坏客户),没有逾期和逾期不超过20天的客户标签y定义为0(好客户)。
data.y.value_counts()
结果:
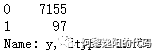
本文总计样本数量为7252,其中7155个样本是好客户,97个样本是坏客户。说明0和1的分布很不均匀,我们统计一下占比:
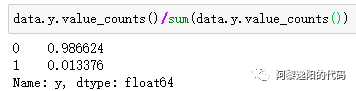
 。
。3.3用describe函数查看数据分布
data.describe()
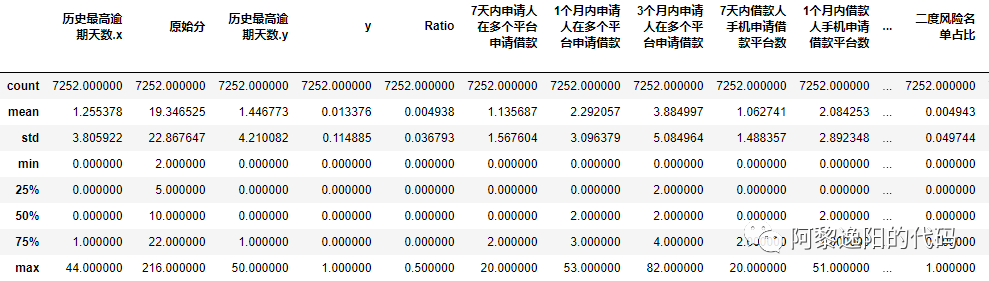
1.甄别变量是否存在缺失值。count的结果是该变量中非空值的个数,如果某个变量count值和样本个数不等,说明该变量存在缺失值,样本个数和count值的差值即为该变量缺失值个数。 2.判断某个变量是否存在数据错误。由于describe中有变量最小值和最大值的信息,可以分析该值是否符合常识来判断变量是否正确。比如人的年龄不可能是个负数,如果年龄中存在负数说明该变量数据出现错误。
3.分析样本在某个变量上是不是有集中性。比如上图中历史最高逾期天数这个变量,从describe结果可发现50%分位数的值为0,75%分位数的值为1,最大值为44。说明50%以上的客户从未逾期,75%的客户从未逾期或逾期不超过1天,说明在该变量上,样本集中在没有逾期这一档。
4.分析好坏客户的样本分布是否差别很大。可以把数据集分成标签为1和0的子集,分别看子集中describe的结果。
 ,本文着重讲逻辑回归的实现,故后文不再在细枝末节处做过多说明。有小细节需要注意的地方,我会在后续文章中分专题详细阐述。
,本文着重讲逻辑回归的实现,故后文不再在细枝末节处做过多说明。有小细节需要注意的地方,我会在后续文章中分专题详细阐述。4 用IV挑选变量
等频计算IV的函数如下:
#等频切割变量函数def bin_frequency(x,y,n=10): # x为待分箱的变量,y为target变量.n为分箱数量total = y.count() #1 计算总样本数bad = y.sum() #2 计算坏样本数good = total-bad #3 计算好样本数if x.value_counts().shape[0]==2: #4 如果该变量值是0和1则只分两组d1 = pd.DataFrame({'x':x,'y':y,'bucket':pd.cut(x,2)})else:d1 = pd.DataFrame({'x':x,'y':y,'bucket':pd.qcut(x,n,duplicates='drop')}) #5 用pd.cut实现等频分箱d2 = d1.groupby('bucket',as_index=True) #6 按照分箱结果进行分组聚合d3 = pd.DataFrame(d2.x.min(),columns=['min_bin'])d3['min_bin'] = d2.x.min() #7 箱体的左边界d3['max_bin'] = d2.x.max() #8 箱体的右边界d3['bad'] = d2.y.sum() #9 每个箱体中坏样本的数量d3['total'] = d2.y.count() #10 每个箱体的总样本数d3['bad_rate'] = d3['bad']/d3['total'] #11 每个箱体中坏样本所占总样本数的比例d3['badattr'] = d3['bad']/bad #12 每个箱体中坏样本所占坏样本总数的比例d3['goodattr'] = (d3['total'] - d3['bad'])/good #13 每个箱体中好样本所占好样本总数的比例d3['WOEi'] = np.log(d3['badattr']/d3['goodattr']) #14 计算每个箱体的woe值IV = ((d3['badattr']-d3['goodattr'])*d3['WOEi']).sum() #15 计算变量的iv值d3['IVi'] = (d3['badattr']-d3['goodattr'])*d3['WOEi'] #16 计算IVd4 = (d3.sort_values(by='min_bin')).reset_index(drop=True) #17 对箱体从大到小进行排序cut = []cut.append(float('-inf'))for i in d4.min_bin:cut.append(i)cut.append(float('inf'))WOEi = list(d4['WOEi'].round(3))return IV,cut,WOEi,d4
columns_x =['7天内申请人在多个平台申请借款','1个月内申请人在多个平台申请借款','3个月内申请人在多个平台申请借款','7天内借款人手机申请借款平台数','1个月内借款人手机申请借款平台数','3个月内借款人手机申请借款平台数','7天内借款人身份证申请借款平台数','1个月内借款人身份证申请借款平台数','3个月内借款人身份证申请借款平台数','7天内关联P2P网贷平台数','1个月内关联P2P网贷平台数','3个月内关联P2P网贷平台数','7天内申请人关联融资租赁平台数','1个月内申请人关联融资租赁平台数','3个月内申请人关联融资租赁平台数','1个月内申请人关联一般消费分期平台数','3个月内申请人关联一般消费分期平台数','风险名单占比','一度关联节点个数','二度关联节点个数','一度风险名单个数','二度风险名单个数','一度风险名单占比','二度风险名单占比','X3个月内申请人手机号作为第二联系人手机号出现的次数','X3个月内申请人手机号作为前三联系人手机号出现的次数','是否命中法院执行模糊名单','是否命中法院结案模糊名单','是否命中手机风险关注名单','是否命中身份证风险关注名单','命中中风险关注名单笔数','客户异常借款笔数','信用异常笔数','执行标的','申请人执行标的是否超过100000','3个月手机号关联身份证数','3个月身份证关联手机号数','三个月银行相关平台数'] #自变量名称X = data[columns_x] #生成自变量数据框Y = data['y'] #生成因变量y
再用调用等频法算IV的函数,计算单个变量的IV值,并打印结果。
IV,cut,WOEi,d4 = bin_frequency(X['1个月内申请人在多个平台申请借款'], Y)print('IV=',IV)d4
得到结果:
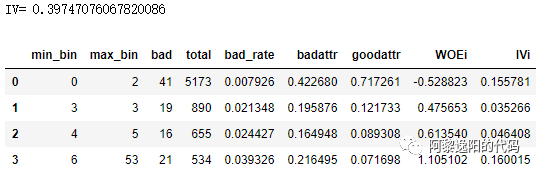
可以用如下语句批量计算变量的IV值,并打印每个变量的分箱woe情况:
ivs=[]for i in columns_x:print(i)IV,cut,WOEi,d4 = bin_frequency(X[i], Y)print('IV=', IV)ivs.append(IV)print(d4)
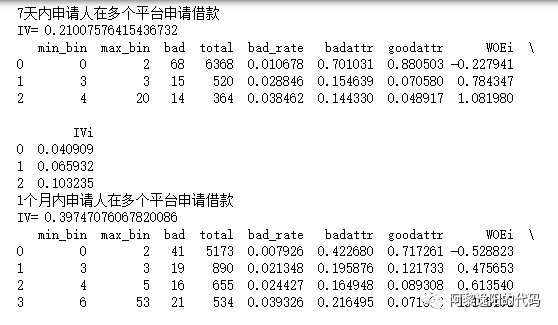
IVi=pd.DataFrame({'name':columns_x, 'IV':ivs}).sort_values('IV',ascending = False)IVi.to_csv("IV.csv")
得到结果(部分截图):
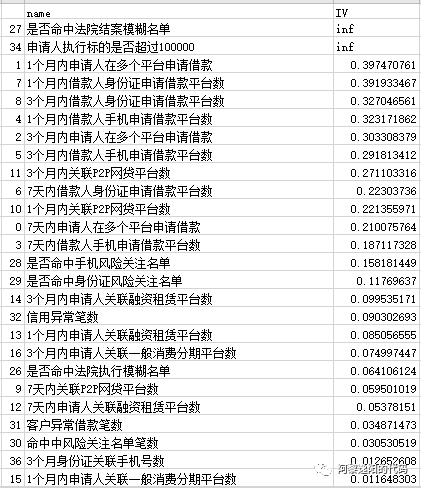
columns_model = ['1个月内借款人身份证申请借款平台数','7天内关联P2P网贷平台数','3个月内关联P2P网贷平台数','3个月手机号关联身份证数','3个月内申请人关联融资租赁平台数','二度风险名单个数','是否命中身份证风险关注名单','原始分','一度风险名单个数']X_model = data[columns_model] #生成入模自变量y = data['y'] #生成入模因变量 from sklearn.linear_model import LogisticRegression as lr #导入逻辑回归库lr_model_1 = lr() #调用逻辑回归lr_model_1_y = lr_model_1.fit(X_model, y) #用样本数据训练逻辑回归模型y_proba_model_1 = lr_model_1_y.predict_proba(X_model) #用训练好的模型预测y_proba_model_1
得到结果:
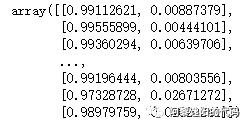
可以用如下语句得到模型的系数和截距:
lr_model_1_coef = pd.DataFrame(lr_model_1_y.coef_)lr_model_1_coef.columns = columns_model

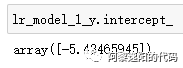
在建完原始模型后一般要把变量转成woe后,再用逻辑回归训练一次变量,得到相应的系数。因为把变量转成woe后变量具有更好的鲁棒性,模型会更加稳定。
由于篇幅问题,在本文中只给转出转woe后建模的结果:
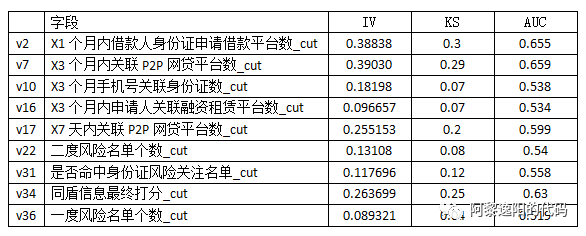
把变量转成woe后,可以根据分箱情况和逻辑回归的结果,通过转换把变量变成评分卡的形式:
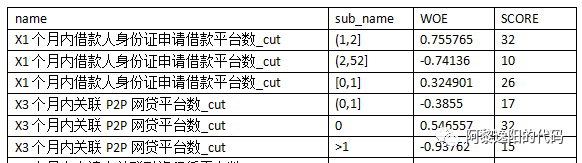
 。
。https://blog.csdn.net/lc574260570/article/details/82116197https://blog.csdn.net/laobai1015/article/details/80512849https://blog.csdn.net/weixin_41712499/article/details/82526483https://blog.csdn.net/qq_27972567/article/details/81949023?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-4&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-4







