
我的新课《C2C 电商系统微服务架构120天实战训练营》在公众号儒猿技术窝上线了,感兴趣的同学,可以长按扫描下方二维码了解课程详情:
课程大纲请参见文末

Leetcode算法题哟~
简介 金融里的二叉树 树的所有概念a. 树的三大特点b. 树的五大品种c. 高度和深度 看树的角度a. 三种 DFS
遍历方式b. 两种BFS
遍历方式c. 四种视图
简介
在这片森林里,最常用的还是「二叉树」
二叉树,是由很多个 TreeNode
构成的这种树形的数据结构,
class TreeNode { int value; TreeNode left; TreeNode right;}
就像链表中的 ListNode
。
二叉树并不一定非得是“二叉”的,而是说每个节点最多有两个孩子,叫 left
和 right
,但也可以没有。
当每个节点都只有一个孩子的时候,就退化成了链表。
所以链表就是一棵特殊的树,而树是一个特殊的图。
金融里的二叉树
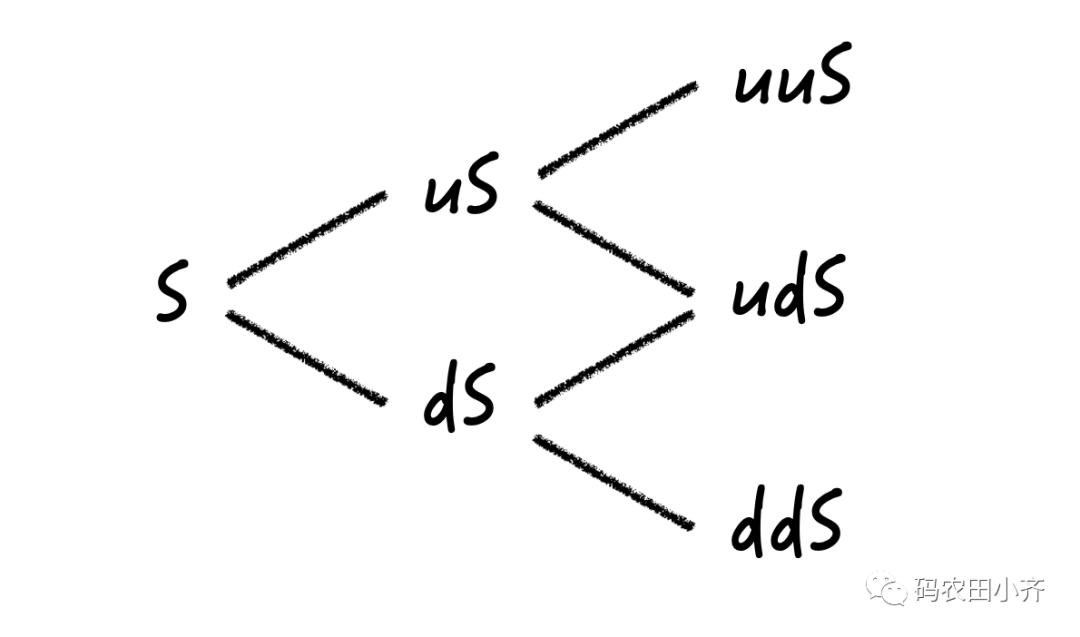
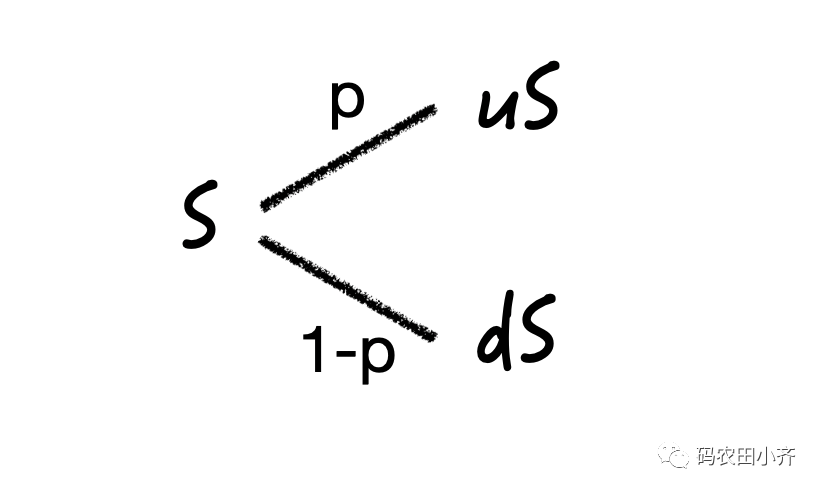
S,那我们想知道未来某个时刻比如
t 时刻的价格,股价有可能上涨也有可能下跌,还可能不变呢。
p的概率上涨至
uS,有
1-p的概率下跌至
dS.
p并不是在真实世界里股票上涨的概率,而是一个在风险中性世界里的上涨概率,所以
树的所有概念
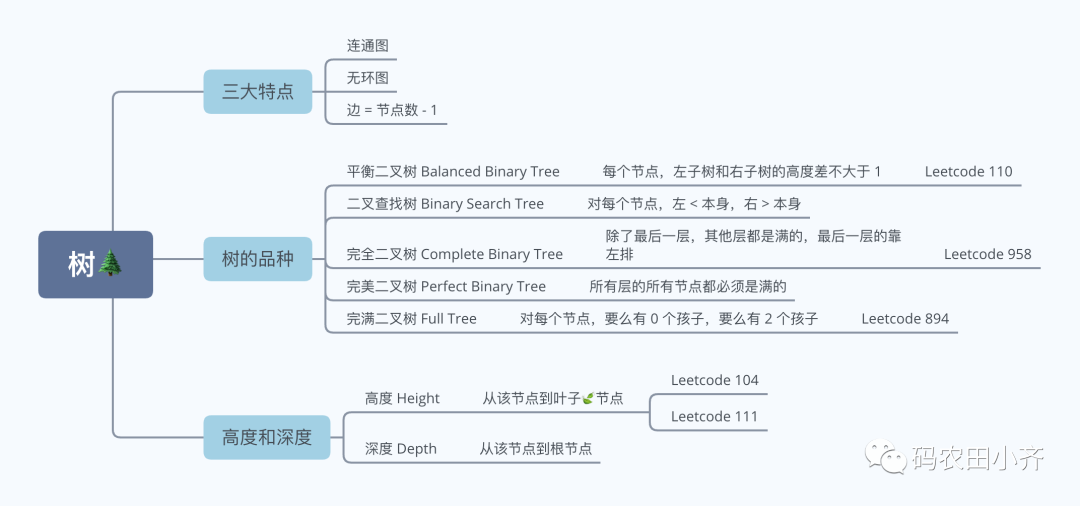
1. 三大特点
如果把树看成一个无向图,那么它是一个连通图 connected graph
.树是一个无环图。 树的节点个数和边的个数之间的关系是固定的。如果树上有 n
个node
,那么它有n-1
条边。因为除了根节点,其他的节点都会有一条边指向它。
2. 树的品种
Balanced Binary Tree:
定义:对于这棵树里的每个节点,它的左子树和右子树的高度差不大于 1。
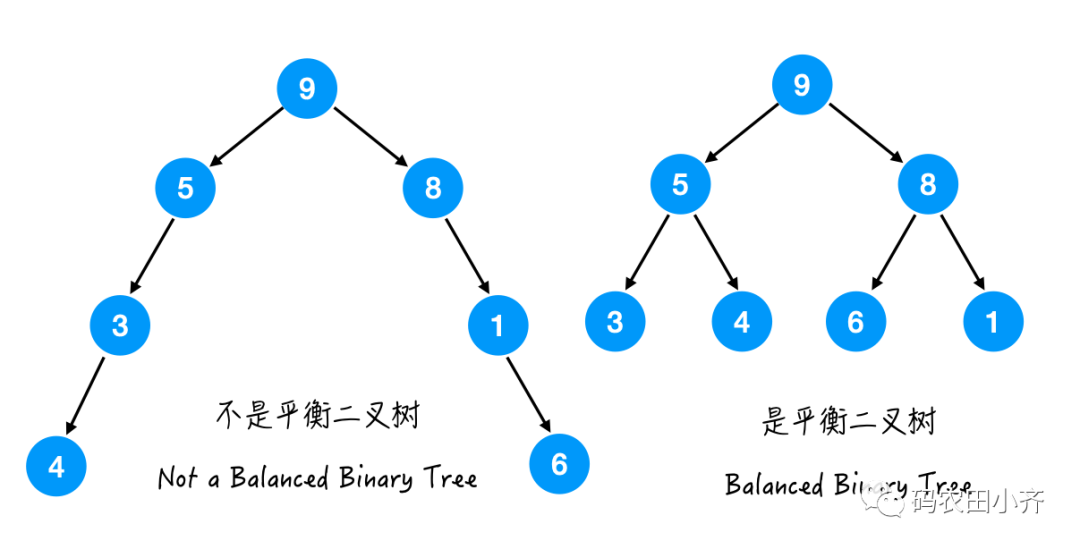
AVL-Tree就是平衡二叉树,准确说是自平衡二叉查找树。
Binary Search Tree定义:对于这棵树里的每个节点, 它左子树里的每个节点的值都小于它的值; 它右子树里的每个节点的值都大于它的值。
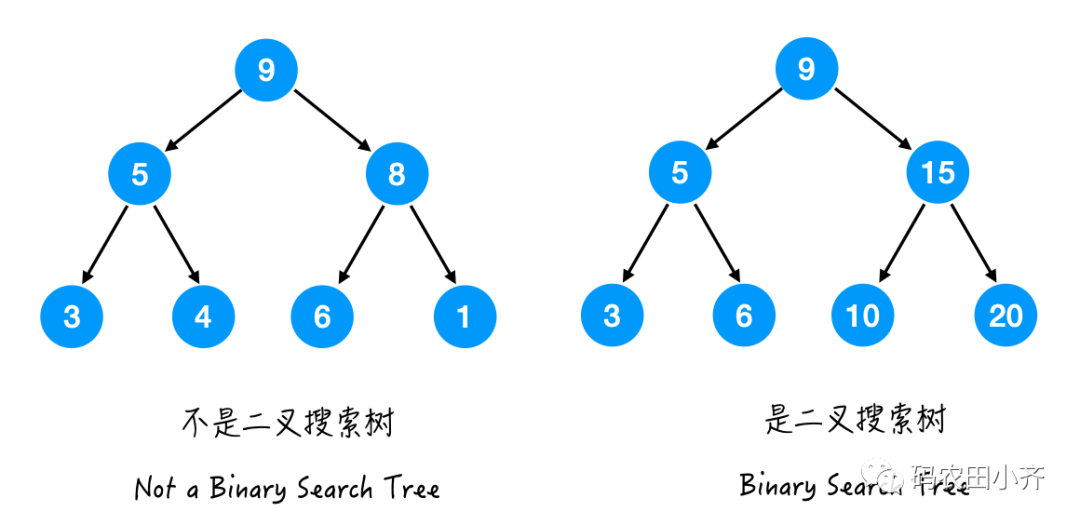
Complete Binary Tree:
定义:除了最后一层,其他层都是满的,那么最后一层的节点要靠左排列且中间不允许有气泡。
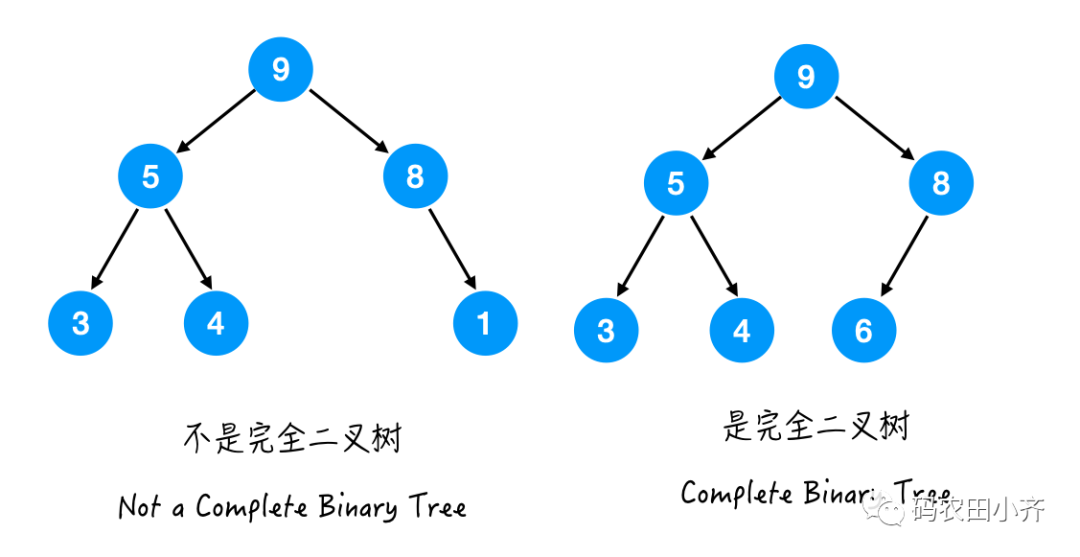
Perfect Binary Tree定义:所有层的所有节点都必须是满的。
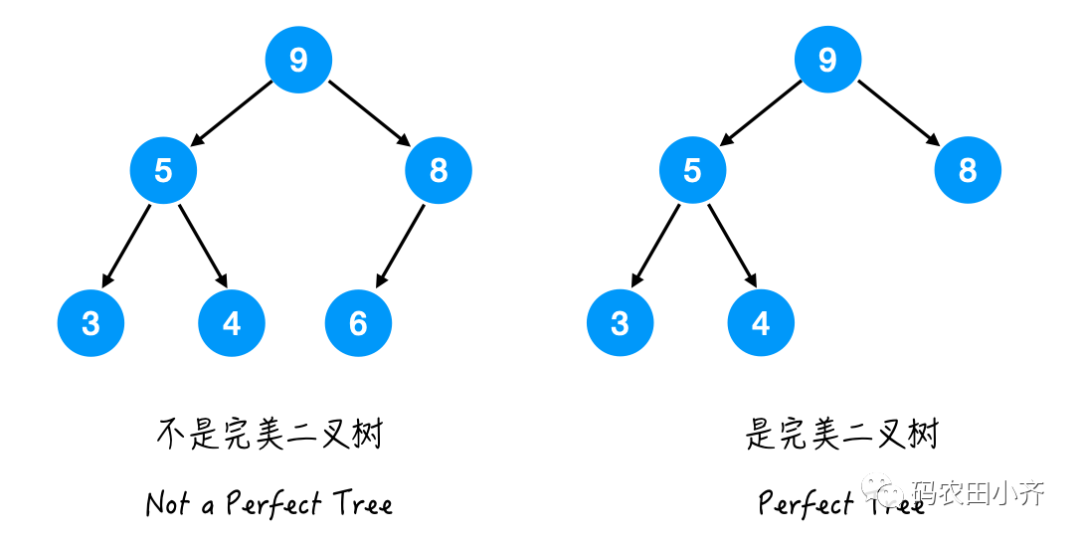
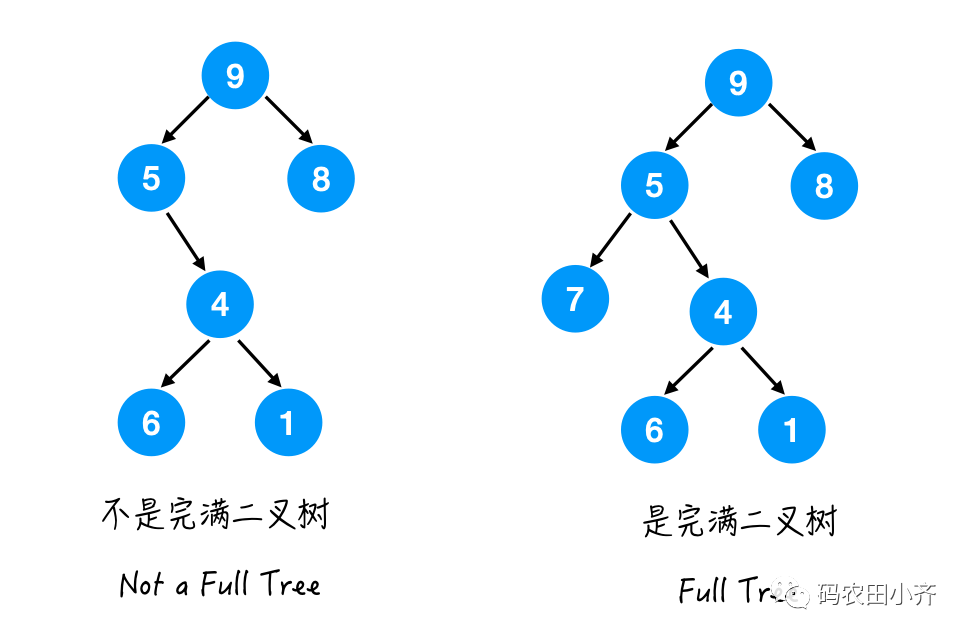
Full Tree定义:对于这棵树的每个节点而言,要么有 0 个孩子,要么有 2 个孩子。
3. 高度和深度
height和深度
depth是两个非常重要的概念,比如 Leetcode 104 和 111 就是专门求树的高度的。
高度是从当前节点到叶子 🍃 节点的; 深度是从当前节点到根 🌲 节点的。
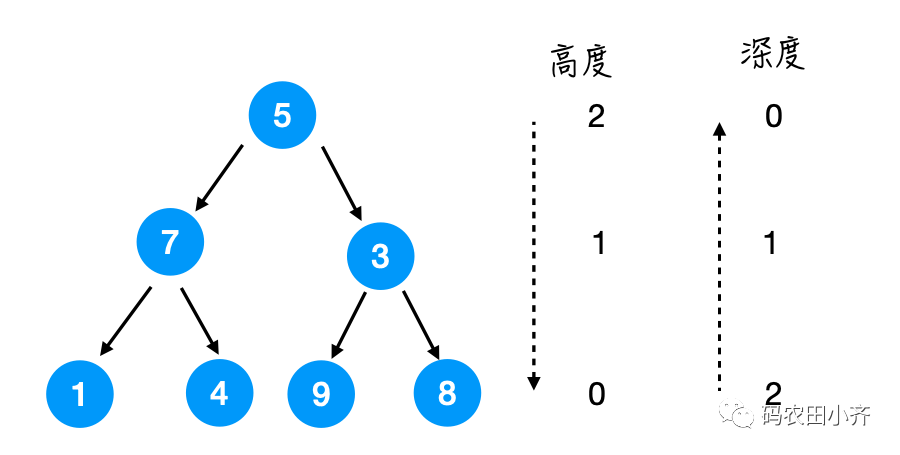
Height定义:从该节点,到以该节点为根节点的这棵树的最远的叶子结点的最长距离。
call stack上有多少层。
Depth定义:从这个节点到根节点的距离。
看树的角度
left/right/vertical/border view,也就是求树的左视图、右视图、俯视图、border view 这我没找到中文翻译。。这就是我所说的「峰」。
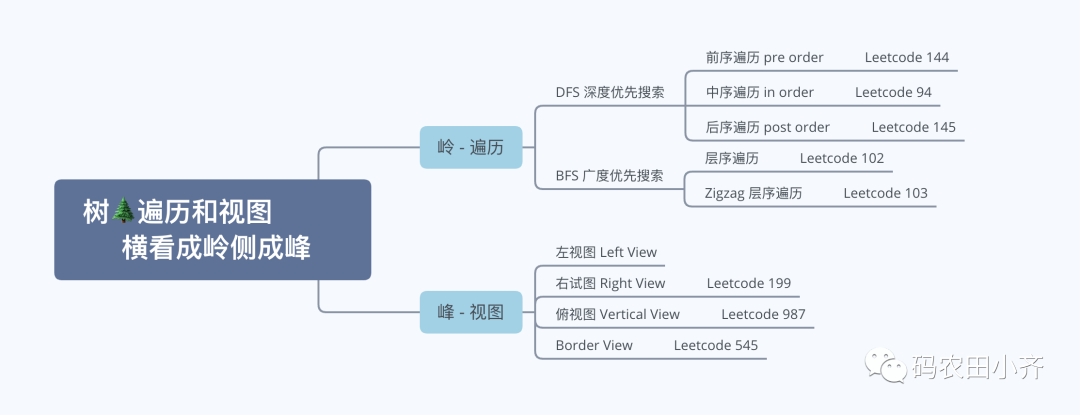
岭
前序 pre order中序 in order后序 post order
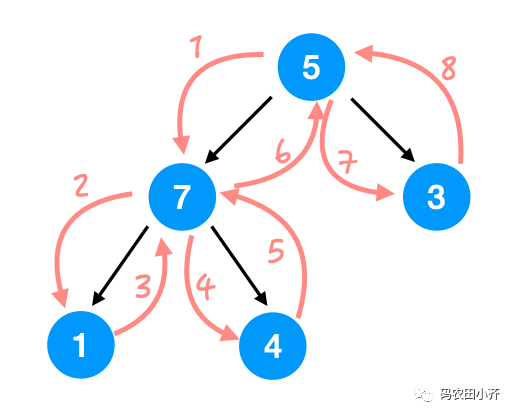
public void traverse(TreeNode node) { if (root == null) { return; } //preOrder print(root.value); traverse(root.left); //真正的遍历 //inOrder print(root.value); traverse(root.right); //真正的遍历 //postOrder print(root.value);}
DFS,而层序遍历是广度优先遍历
BFS。
DFS和
BFS都是图的基本遍历方式,我之后也会专门写一篇。
level order traversal。
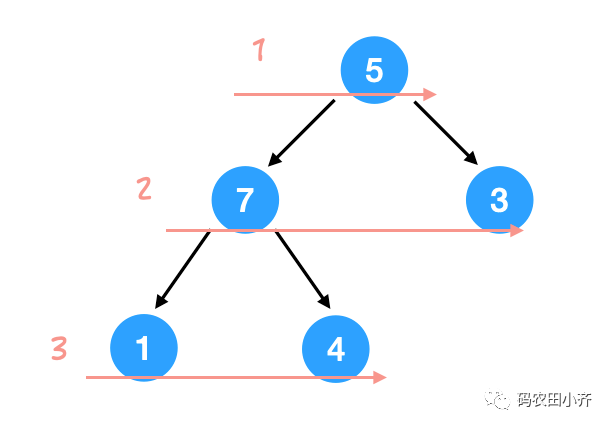
5 7 3 1 4.
Zigzag的遍历方式,就是一行从左到右,下一行从右到左这样子。
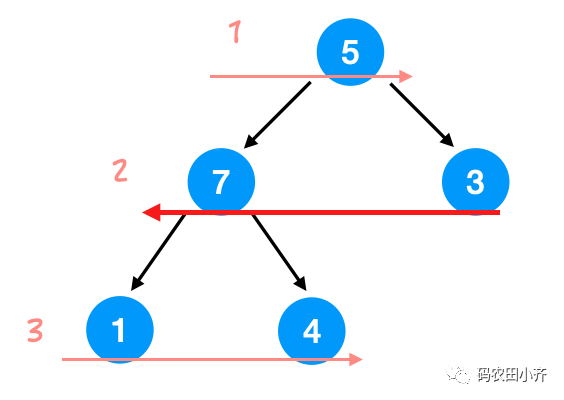
5 3 7 1 4.
峰
left/right/vertical/border view,也就是求树的左视图、右视图、俯视图,是非常爱考的一类题,它们是什么意思呢?
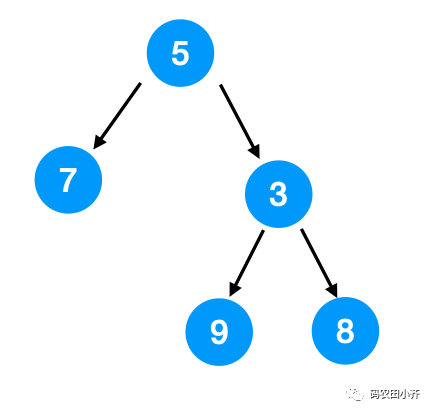
left view:
就是从左边看的每层的第一个节点。 [5, 7, 9]
right view:
就是从右边看的每层的第一个节点。 [5, 3, 8]
column,根节点为 0,左孩子 - 1,右孩子 + 1。
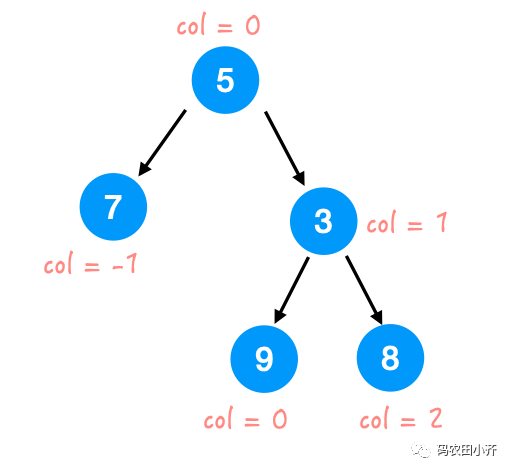
[[7], [5, 9], [3], [8]]border view想必大家都能猜出来意思了。
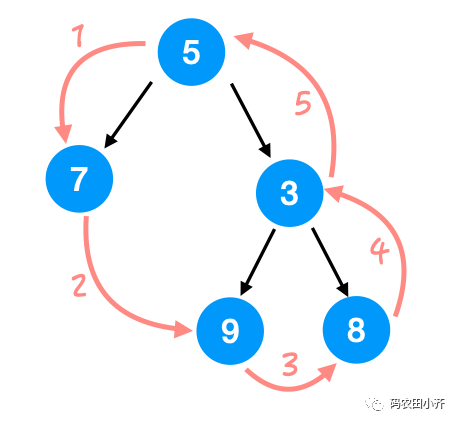
border view就是:
5, 7, 9, 8, 3clarify很多细节。
END




文章转载自石杉的架构笔记,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。







