Kaggle知识点：时序数据DTW距离

DTW（Dynamic Time Warping）是一种能够很好衡量序列相似度的方法，在竞赛中可以用于计算序列相似度，构造序列特征，本文将对其原理的使用进行介绍。

序列距离计算

假设时间序列由多个时间采样的数据点构成，此时在给定查询序列的情况下，需要从数据集中找到最为相似的序列。

常规的方法是使用欧几里得距离Euclidean distance (ED)，或皮尔逊系数完成相似度计算。

上图的阴影部分与的欧几里得距离。此时两段序列如果为两段音频，不同人的语速不同，音频的峰值会出现不同程度的偏移。如果这时还是用欧几里得距离，会出现计算误差，不能够比较真正程度上的相似性。

DTW原理

DTW是解决上述时序序列速度不一致性的有效方法，借助序列值的对齐操作来完成。DTW将序列进行延伸和缩短，来计算两个时间序列性之间的相似性，如下图所示：

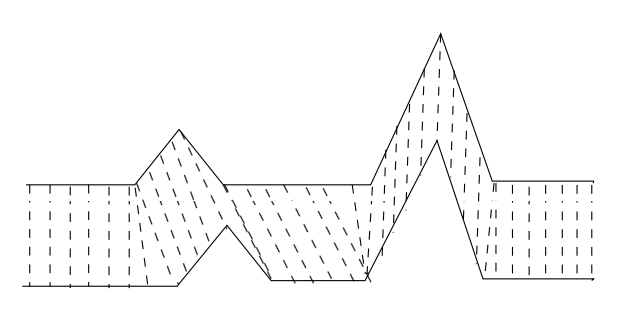
实线代表两个时间序列，虚线代表两个序列之间的相似的点。DTW使用所有这些相似点之间的距离的和，称之为归整路径距离(Warp Path Distance)来衡量两个时间序列之间的相似性。

DTW实现

DTW将两个序列对齐问题转化为二维平面中最优路径的问题。横纵坐标分别表示两个序列，通过对齐操作我们可以绘制出最优路径。路径的选择是一个动态规划的问题。

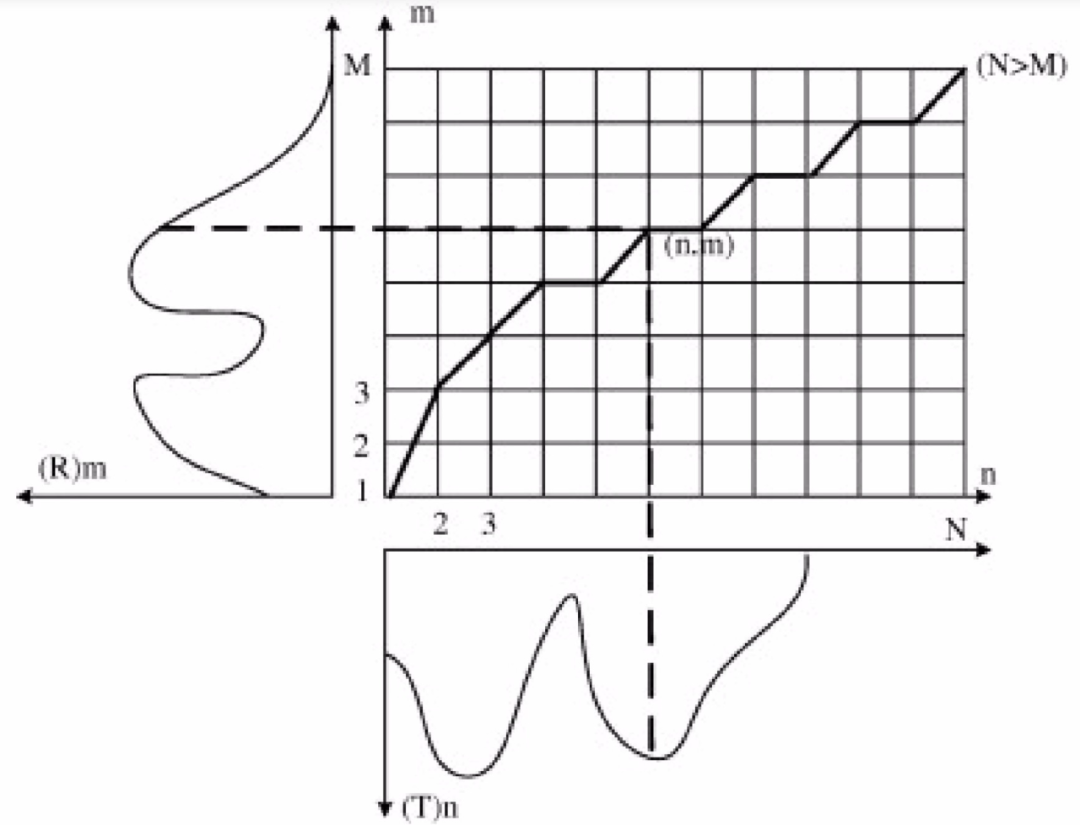
# DTW的核心过程，实现动态规划
def dtw(s, t):
    
    # s: source sequence
    # t: target sequence
    
    m, n = len(s), len(t)
    dtw = np.zeros((m, n))
    dtw.fill(sys.maxsize)
    
    # 初始化过程
    dtw[0,0] = euc_dist(s[0], t[0])
    for i in range (1,m):
        dtw[i,0] = dtw[i-1,0] + euc_dist(s[i], t[0])
    for i in range (1,n):
        dtw[0,i] = dtw[0,i-1] + euc_dist(s[0], t[i])
    
    # 核心动态规划流程，此动态规划的过程依赖于上面的图
    for i in range(1, m): # dp[][]
        for j in range(max(1, i- 10), min(n, i+10)):
            cost = euc_dist(s[i], t[j])
            ds = []
            ds.append(cost+dtw[i-1, j])
            ds.append(cost+dtw[i,j-1])
            ds.append(2*cost+dtw[i-1,j-1])
            ds.append(3*cost + dtw[i-1,j-2] if j>1 else sys.maxsize)
            ds.append(3*cost+dtw[i-2,j-1] if i>2 else sys.maxsize)
            # pointer 
            dtw[i,j] = min(ds)
    
    return dtw[m-1, n-1]

当然如果想用优化后的DTW库，推荐dtw-python
：

pip install dtw-python

import numpy as np

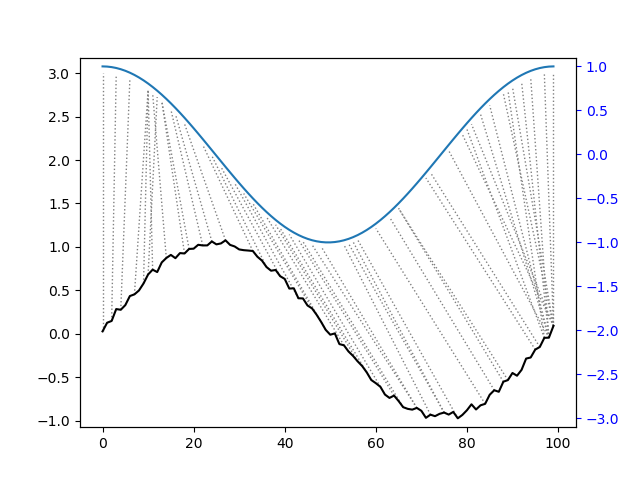
## A noisy sine wave as query
idx = np.linspace(0,6.28,num=100)
query = np.sin(idx) + np.random.uniform(size=100)/10.0

## A cosine is for template; sin and cos are offset by 25 samples
template = np.cos(idx)

## Find the best match with the canonical recursion formula
from dtw import *
alignment = dtw(query, template, keep_internals=True)