前言
《Advancing mathematics by guiding human intuition with AI》

前段时间,DeepMind团队与几位数学家一起,将人工智能应用在了数学的两个分支领域——拓扑学和表示论,并为数学家发现猜想和定理提供了一种新的辅助工具,能够有效辅助数学研究。该项工作发表在Nature期刊上,论文名称为《Advancing mathematics by guiding human intuition with AI》。由于该论文基于基础数学的研究,为了帮助读者更好地理解,笔者将简要梳理下所涉及的数学知识,对此感兴趣的读者可在阅读完此文之后继续阅读相关参考文献。
拓扑学
论文中涉及到拓扑学中的纽结理论(knot theory),纽结理论本质上就是研究“绳结”的理论。假设我们手中有一条绳子,不考虑绳子的粗细、长短、软硬、曲直等因素,只在意绳结的结构,也就是绳子是如何穿插的。现在打好一个结后,为了避免结构发生变化,我们将绳子的两头系在一起,这样就形成了一个纽结,这个结叫做“三叶结”。
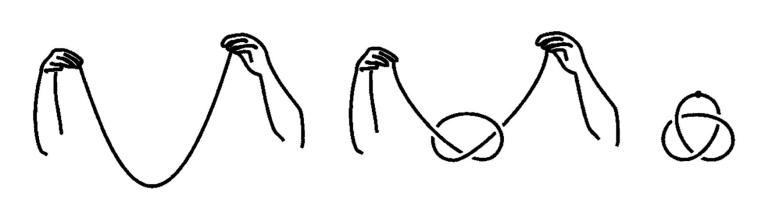
在纽结理论中,一个纽结只要不被剪断,或是把纽结上不同的点粘连在一起,那么对纽结做任意拉伸、扭转、弯曲等变换,得到的都是同一个纽结。比如下图中的三个纽结,虽然看起来不同,实际上是同一个纽结。
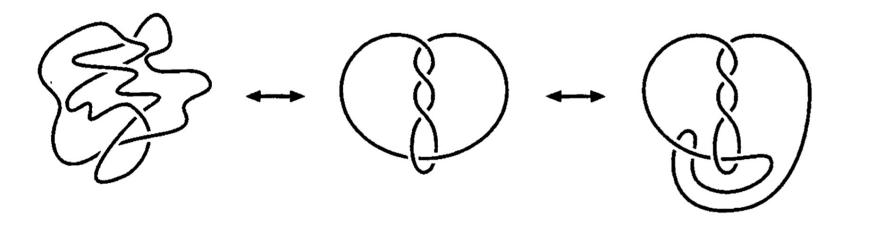
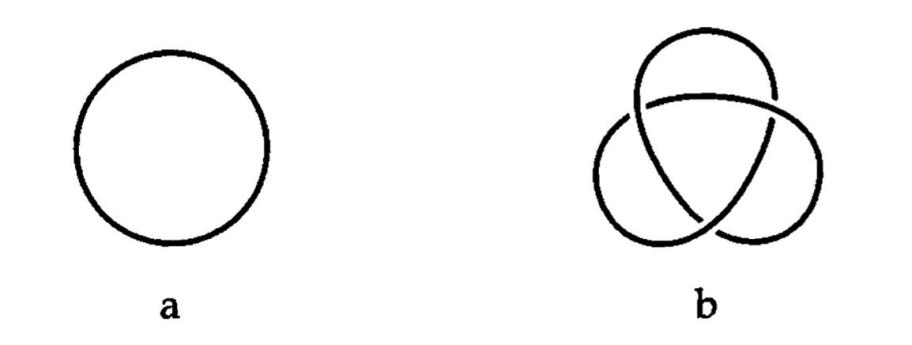
那我们如何知道两个纽结是不是一样的呢?对于简单的纽结,读者可以拿两根线试一试,如下图,左边的a图是一个圆,在纽结理论中这是最简单的纽结,叫做“平凡结”,右边的b图是三叶结。可以发现,在不借助剪刀和胶水的情况下,无论怎么扭转三叶结,始终无法变成平凡结,所以平凡结和三叶结是两个不同的纽结。
不过对于复杂的纽结,只依靠动手尝试无法判断它们是不是同一个纽结,这就是纽结理论研究的最基本的问题——给定两个纽结,怎么判定它们是不是同一个纽结?换句话说,如何对纽结进行分类。
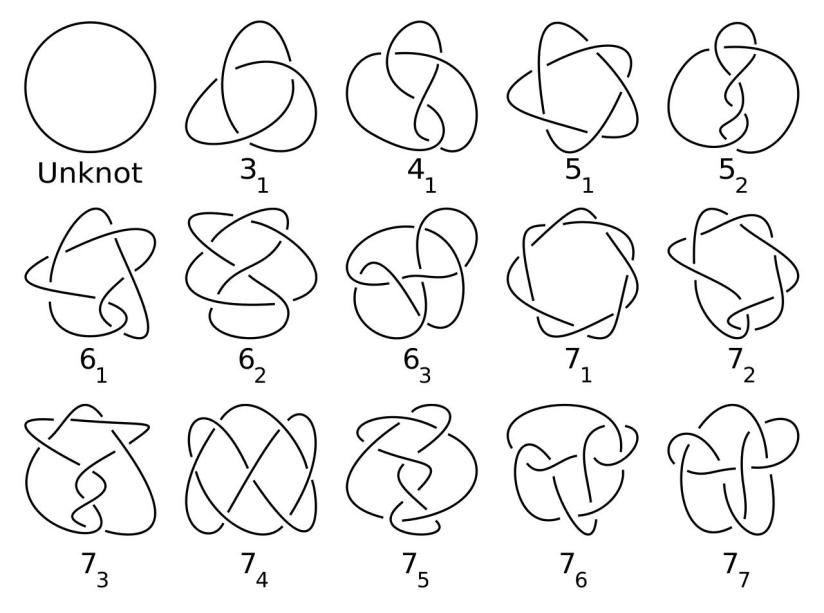
同一个纽结,形状可以千变万化,解决问题的关键就是寻找千变万化中的对象的某些“不变量”。就像是一个人从小到大,体型发生变化、外貌发生变化、声音发生变化,但是指纹、视网膜是不会发生变化的,这些属性就是不变量,通过不变量可以从茫茫人海中识别出一个特定的人。对于纽结来说,最先能想到的应该就是交叉点的数量了,整理一个纽结,使其交叉点数达到最少,那么这个交叉点数就是一个不变量。如下图,平凡结的交叉点数是0,三叶结的交叉点数是3。不过可惜的是,交叉点数不是一个很好的不变量,因为没有一个很好的方法能够判断一个纽结的交叉点数是否最少,并且,不同的纽结可以有相同的交叉点数,可以看到当交叉点数为5时有2个不同的纽结,交叉点数为6时有3个不同的纽结,交叉点数为7时有7个不同的纽结。
一个好的纽结不变量是1984年新西兰数学家沃恩·琼斯发现的“琼斯多项式”,琼斯也因此在1990年获得了数学界的最高荣誉之一:菲尔兹奖。琼斯多项式的具体推导方式不在这里扩展了,感兴趣的读者可以阅读参考文献[1]。当然了,还有许多其他的不变量,论文中涉及的另一个不变量是“符号差(signature)”,这些都属于代数不变量,也就是用代数的方法来研究几何问题。除了用代数的方法,同样还有许多其他不同的推导方法,论文关注的另一个方法是双曲不变量(也叫几何不变量),包括经度、纬度、体积等等,体现的是纽结的几何特征。代数不变量和双曲不变量是两种完全不同的表征纽结的方法,论文的成果之一就是通过神经网络,找出了代数不变量中的符号差与双曲不变量之间的关系。
表示论
数学中有个很重要的思想——化简,即把庞杂的知识分解成简单的知识点,把不熟悉的东西用熟悉的东西去解释、描述。这也正是表示论(representation theory)的思想核心,表示论是将代数结构中的元素“表示”成向量空间上的线性变换,以此来研究结构性质的理论。表示论中比较系统的一块是群表示论(group representation theory),简单来说,群(group)是按照某种规律相互联系着的一组元素的集合,群表示论是用矩阵来展示群的结构,进而描述群的理论。
本篇论文的主要对象是对称群(symmetric groups),可以从排列的思想中产生对称群[2]。假设有5个元素,将元素2、3进行对换,那么排列可以表示成以下形式:
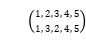
第一行表示元素的编号,第二行表示排列后映射到的元素:将元素2映射到元素3,将元素3映射到元素2,将元素1、4、5映射到自身。这种表示不够简洁,因此有另一种表示方法:
以
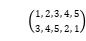
为例,将元素1映射到元素3、元素3映射到元素5、元素5映射到元素1表示为(1, 3, 5),将元素2映射到元素4、元素4映射到元素2表示为(2, 4),那么整体就表示为(1, 3, 5)(2, 4),如果是
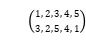
可以表示成(1, 3, 5)(2)(4),因为第2、4个元素没有进行任何变化,因此可以省略不写,于是结果表示为(1, 3, 5)。排列与群的概念非常吻合,排列满足群的所有的性质和定义,因此排列也是群的一种,n个对象所有的排列构成对称群Sn,其中的每一种排列都是对称群Sn的一个群元素。对于对称群中任意两个群元素之间的转换(反射),例如下图S4中的[1234, 4321],可以用Bruhat区间图(一种序结构的图)来表示。
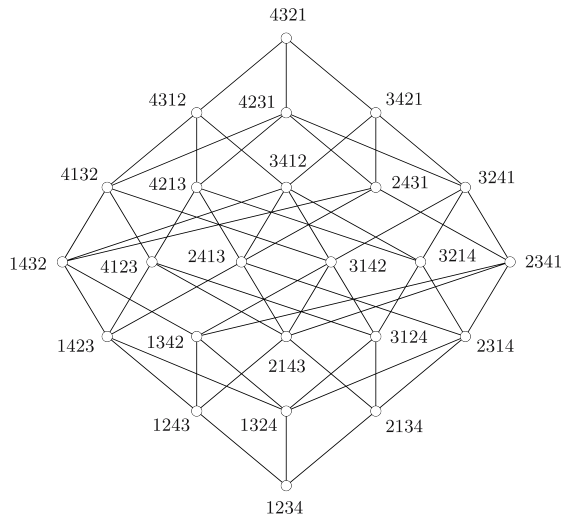
用人工智能指引数学直觉
拓扑学
论文中首先对纽结理论的不变量进行研究。数学家们挑选了12个双曲不变量作为候选不变量,创建了一个包含270万个纽结的数据集,标记了符号差和这12个双曲不变量。利用这些数据集,训练了一个3层全连接的神经网络,其任务是从双曲不变量中预测符号差。他们观察到,训练后的神经网络预测符号差的准确率为78%,这表明,符号差与双曲不变量之间确实存在着某种关系。通过归因技术,在保持准确率的同时将输入减少到三个双曲不变量:longitudinal translation、meridional translation的实部、meridional translation的虚部,如下图所示。
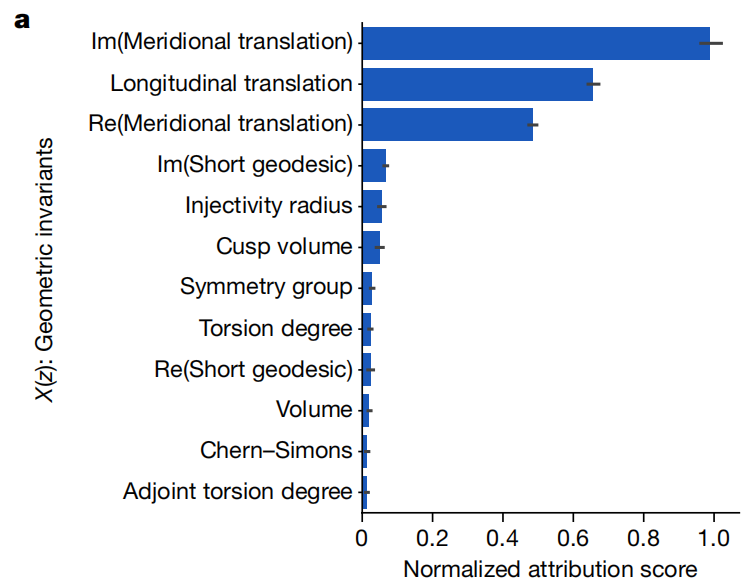
考虑到这三个量的相关性和特殊性,数学家们决定将它们组合成一个新的、有几何意义的量,即“自然斜率(natural slope)”,定义为slope(K)=Re(λ/μ),其中µ是meridional translation,λ是longitudinal translation,Re为实部,符号差用σ(K)表示。结果表明,存在一个近似的线性关系:符号差大约是自然斜率的一半。在自然斜率为符号差的唯一预测特征的情况下,准确率仍为78%,也就是说自然斜率继承了12个双曲特征的所有预测能力,于是他们提出了一个关于自然斜率和符号差的初步的猜想:
猜想:存在常数c1和c2,使得对于每个双曲纽结K,有
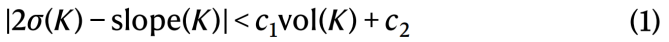
其中vol(K)是双曲纽结K的体积,是12个双曲不变量之一。
数学家们意识到,对于一些特定的纽结,可能存在初步猜想的反例。他们生成了一个包含大约36,000个纽结的数据集,从中确实发现了一些反例。之后对初步猜想进行修正,提出了以下定理,并在参考文献[3]中进行了完整证明:
定理:存在一个常数c使得对于任何双曲纽结K,有
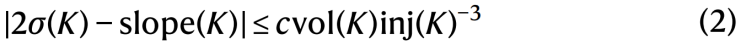
其中inj(K)是注入半径(injectivity radius),也是12个双曲不变量之一,可以是一个很小的实数。
上述定理找到了纽结的代数和几何结构之间的新的联系,这个发现在低维拓扑中能够有许多其他的应用。不可思议的是,在这之前,在纽结理论这种被广泛研究的领域中,这样一个简单而重要的联系却被忽视了。
表示论
与纽结理论一样,表示论的成果也是对一个数学对象的两种不同表示的连接。这一部分的研究对象是对称群,这是代数结构中非常重要的一个范畴。一个对称群的两个群元素之间的关系可以用两种不同的方式来表征:Bruhat区间图和Kazhdan-Lusztig(KL)多项式。由上文可知,当n=4时,S4的群元素有4!=24个,当n=5时,S5的群元素有5!=120个,Sn的群元素数量是成阶乘增长的。也就是说,随着n的增加,Bruhat区间图会变得相当复杂,当n增加到9时,S9的群元素数量就能达到9!=362,880个,相比较来说,KL多项式的表达就要简单得多(最高项仅为四次幂)。下图是S5和S6的两个群元素对的未标记的Bruhat区间图(一个有向图)和KL多项式的示例。
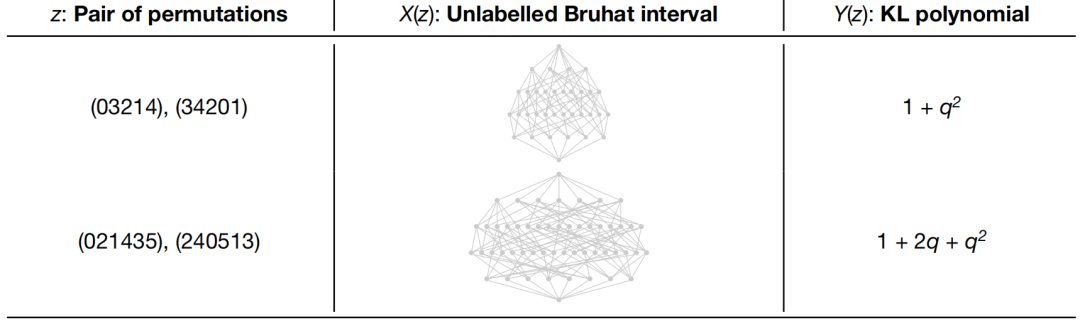
KL多项式中一直存在一个“组合不变性”猜想,它指出,对称群Sn中两个群元素的KL多项式可以由它们未标记的Bruhat区间计算出来。而证明此猜想的难点之一正是Bruhat区间图的庞杂性,研究人员很难对它们的结构产生直观的感觉。
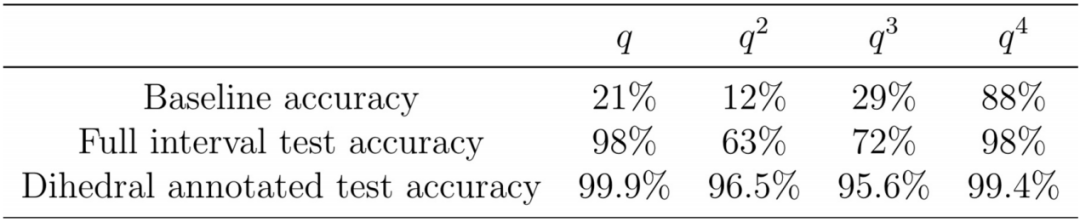
数学家们将此猜想作为初始猜想,创建了一个包含24,000个群元素对的训练集,标记了Bruhat区间图和KL多项式,设计了一个图神经网络,以Bruhat区间图作为输入,以KL多项式的系数作为输出。结果如下图所示,图神经网络能够以相当高的准确度从Bruhat区间预测KL多项式系数,四个系数的准确率在63%到98%之间。同时可以观察到,选择一些特定的图形和特征路径,明显有助于提高预测的准确性。数学家们发现,受先前工作[4]启发的显著子图就足以计算KL多项式,这一发现得到了更精确的估计函数的支持,四个系数的准确率达到了95.6%到99%之间。
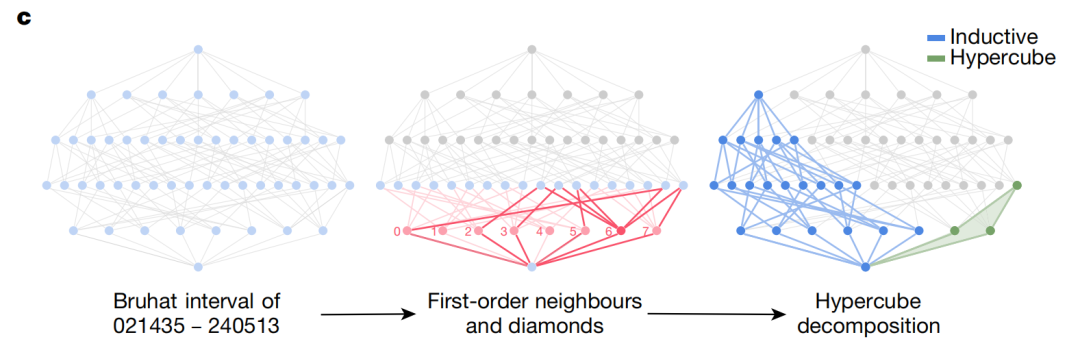
通过分析图神经网络,他们发现了极值反射(extremal reflections,对于Sn来说形式为(0,i)或(i,n−1))在显著子图(下图中红色部分)中出现的频率比预期的要高,而简单反射(simple reflections,形式为(i, i+ 1))出现的频率比预期的要低,数学家们说,他们之前根本没有预料到这一点,不清楚为什么极值反射会在显著子图中超预期出现。
考虑到这一观察结果,他们发现一个Bruhat区间图能够自然地分解为两部分——一个由一组极值反射构成的超立方体(hypercube,下图中绿色部分),和一个与Sn-1区间同构的图(下图中蓝色部分)。
由此,数学家们提出了一个重要的定理:
定理:每个Bruhat区间都允许沿其极值反射进行规范的超立方体分解,从中可以直接计算出KL多项式。
也就是说,有一种方法可以对Bruhat区间图进行预处理,称之为“沿着其极值反射的超立方体分解”,一旦你这样做了,就可以用一个简单的公式,直接从超立方体和Sn-1组件中计算出KL多项式,参考文献[5]中给出了这一定理的详细证明过程。
唯一的问题是,沿着极值反射可能会有许多不同的超立方体分解,然而参考文献[5]中所证明的只是其中一种有效,并没有给出找到正确答案的方法。不过,进一步的测试验证了,对于直到对称群S7的所有大约3×106个区间,和从对称群S8、S9中采样的超过1.3×105个非同构区间,所有超立方体分解都能正确地确定KL多项式。因此,数学家们提出了一个进一步的猜想:
猜想:可以使用前面的公式和任何超立方体分解来计算未标记的Bruhat区间的KL多项式。
如果这个猜想被证实,那就能解决存在40年之久的组合不变性猜想,这是一个很好的研究方向,该猜想不仅在相当大的示例中得到了验证了,而且还拥有一个特别好的形式。
结语
本篇论文从基础数学领域来说,成果令人感到惊艳。在经过充分研究的数学领域中,一些基础性的联系会因为规模过大而无法被观察到,而人工智能可以帮助数学家更好地理解这些联系。本篇论文的创新之处不在于提出什么新方法,而在于为数学工作者提供了一种新的“人机交互”模式,重新划分了“人”与“机”在科研工作中的职责边界,能够更加有效地辅助数学研究。
[参考文献]
[1] 姜伯驹. 绳圈的数学[J]. 1991.
[2] 【群论入门】(10):排列与对称群. [Online]. Available: https://zhuanlan.zhihu.com/p/402197369.
[3] Davies, A., Lackenby, M., Juhasz, A. & Tomašev, N. The signature and cusp geometry of hyperbolic knots. [Online]. Available: https://arxiv.org/abs/2111.15323.
[4] Braden, T. & MacPherson, R. From moment graphs to intersection cohomology. Math. Ann. 321, 533–551 (2001).
[5] Blundell, C., Buesing, L., Davies, A., Veličković, P. & Williamson, G. Towards combinatorial invariance for Kazhdan-Lusztig polynomials. [Online]. Available: https://arxiv.org/abs/2111.15161.

人工智能评测服务
SSTL主要测评内容

上海市计算机软件评测重点实验室(简称SSTL)由上海市科委批准成立于1997年,是全国最早开展信息系统质量与安全测评的第三方专业机构之一,隶属于上海计算机软件技术开发中心。
觉得内容还不错的话,给我点个“在看”呗
我知道你在看哟







