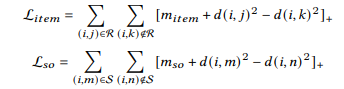点击上方 蓝字关注我们
论文: Where are we in embedding spaces? A ComprehensiveAnalysis on Network Embedding Approaches for Recommender Systems
代码: https://github.com/RinneSz/Social-Collaborative-Metric-Learning
作者:Sixiao Zhang,Hongxu Chen,Xiao Ming,Lizhen Cui,Hongzhi Yin,Guandong Xu


研究问题
双曲空间在图嵌入,图推荐中越来越受关注。但是,目前尚不清楚在什么情况下应考虑双曲空间。为了填补这一空白,本文提供了在推荐系统中什么时候使用双曲空间和双曲嵌入的理论分析和实验结果。
具体来说,作者回答以下几个问题:哪种类型的模型和数据集更适合于双曲空间,以及embedding size对结果的影响。作者通过比较欧氏空间和双曲线空间在一般item推荐域和社会推荐域中不同潜在空间模型上的性能,并使用6个广泛使用的数据集和不同潜embedding size,来进行试验分析。
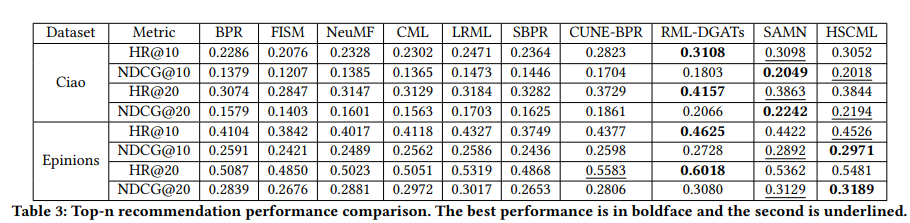
此外,本文提出了一种新的基于度量学习的推荐方法,称为SCML及其双曲线版本HSCML。

实验结论
双曲空间更适合distance-based 的模型;
由于投影模型优化了内积,距离模型优化了距离,因此收敛后嵌入的分布是不同的。对于投影模型,节点之间的关系主要由角度决定。正对的角度很小,负对的角度是钝角。但是,对于距离模型,关系仅由距离决定。正对彼此靠近,负对彼此远离。
如果我们将双曲线空间应用于投影模型,一个问题是,投影模型通常在有限的尺度内对嵌入的范数进行正则化,这使得无法将embedding推离中心很远。所以在双曲线空间中,embedding的范数也会在一个有限的尺度上,难以有效利用容量最大的双曲线空间的外围部分,从而降低表现力。但是,距离模型没有这样的限制,可以利用整个空间。只要精度允许,嵌入可以任意推离原点。距离模型的另一个优点是能够学习分层信息。
双曲空间在低密度的数据上更加的Powerful;双曲线空间能够从数据集中提取层次信息。它可以使用这样的层次结构来帮助更有效地学习节点嵌入。因此,即使密度较低也能有较好的性能。然而,欧几里得空间难以提取层次信息。相反,欧几里得空间需要更多的用户-项目对来帮助达到与双曲线空间相当的性能。也就是说,如果数据集的密度小,那么双曲空间很可能优于欧几里得空间,但如果密度大,欧几里得空间可以有与双曲空间相媲美的性能。(该分析来自论文, 不一定正确)
双曲空间在较小的embedding size上有非常明显的优势
双曲空间的表现力远大于欧几里得空间。例如,当嵌入一种类型的层次结构时,2D 庞加莱圆盘可以有任意小的失真,但 2D 欧几里得空间总会有一些失真 [6]。所以要完全捕获数据集中的所有层次信息,双曲空间所需的维数比欧几里得空间小得多。这就是为什么当潜在尺寸很小时双曲空间应该优于欧几里得空间的原因。另一方面,随着潜在大小的增加,欧几里得空间和双曲空间的性能都有一个上限。此外,它们应该共享相同的上限,因为它们都能够以足够大的潜在尺寸嵌入具有任意低失真的节点。因此,随着潜在大小的增加,它们之间的性能差距应该会减小。最终欧几里得空间将具有与双曲空间相似的性能。
当维度足够大的时候,双曲空间的优势有所下降
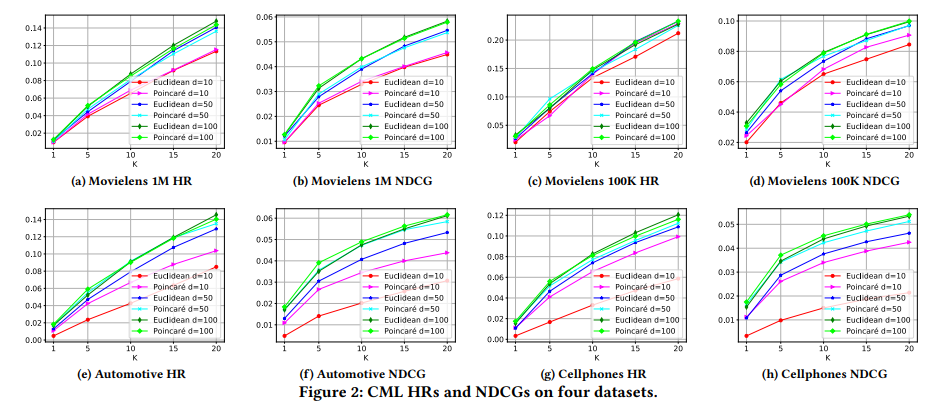
双曲空间在较小的embedding size上有非常明显的优势
当维度足够大的时候,双曲空间的优势有所下降

最后作者提出了一种基于距离的loss function
假设用户-项目正对的集合是R,用户-用户正对的集合是S。对于用户𝑖,采样一个正项𝑗和一个负项𝑘,使得(𝑖, 𝑗) ∈ R, (𝑖 , 𝑘) ∉ R,并采样一个正邻居𝑚和一个负邻居𝑛,使得(𝑖,𝑚) ∈ S, (𝑖, 𝑛) ∉ S。item损失L, 𝑖𝑡𝑒𝑚损失𝑚定义为𝑜