


点击上方 蓝字关注我们
转载请备注:作者知乎号:风雨无阻,
编辑:图与推荐
原文链接:https://zhuanlan.zhihu.com/p/397689557
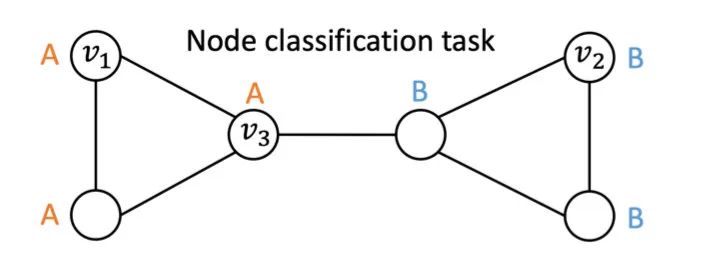
根据(Xu et al., 2019),基于图消息传递架构的GNN的表达能力上限是1-WL图同构测试(1-Weisfeiler-Lehman graph isomorphism test),也就是说,在只使用图结构信息的情况下,这些GNNs不能区分开处于同构位置的两个节点。举个例子,如下图中的节点和有相同的局部邻居结构,GNN会把它们映射到Embedding空间中相同的点上。
下面的三篇文章从不同的角度出发来增强GNN的表达能力。

1. 位置感知图神经网络与结构感知图神经网络
题目:P-GNNs:Position-aware Graph Neural Networks
Position-aware: 如果图节点的Embedding可以保留两个节点在图上的最短路径的信息,我们称这种图节点的Embedding是Position-aware的。
Structure-aware:如果图节点的Embedding是该节点的q阶邻居的函数,那么这种图节点的Embedding是Structure-aware的。
大部分的基于图上的信息传递范式的GNN都是structure aware的,如GCN、GraphSage、GAT等。
作者证明了:仅当图中不存在具有同构q阶邻居的节点对的时候,才存在从structure-aware到position-aware的映射函数。
这其实就是在说,不对GNN进行本质上的改造,是不可能学到position-aware的embeddings的。
作者利用Bourgain Theorem,借助锚点集合的方式,可以从理论上保证空间的弯曲度(distortion)在一定的程度内。从使用锚点集合来作为图上的相对位置的基点,在计算节点的Embedding时融合距离信息,从而学习到带有位置信息的Embedding。
P-GNNs的整体流程如下:
(1)从图上选择k个锚点集合;
(2)计算点关于锚点集合中的点的消息,消息计算函数融合了两个点之间的距离;
(3)聚合点关于锚点集合中的点的消息;
(4)聚合点的所有锚点集合的消息。
P-GNNs的伪代码如下:

几个关键点:

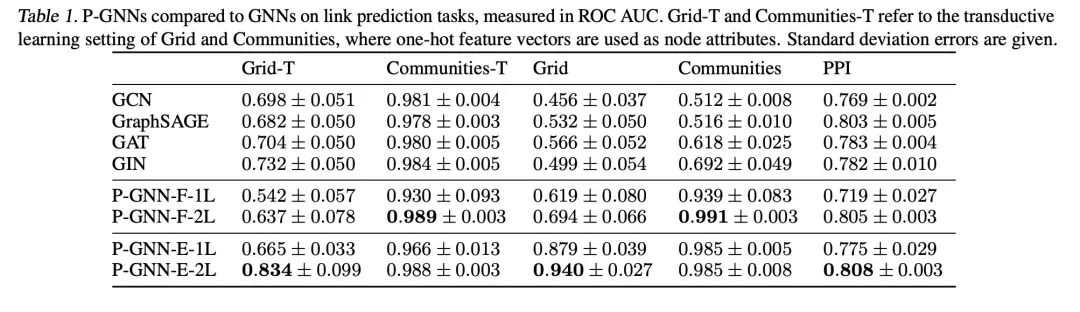
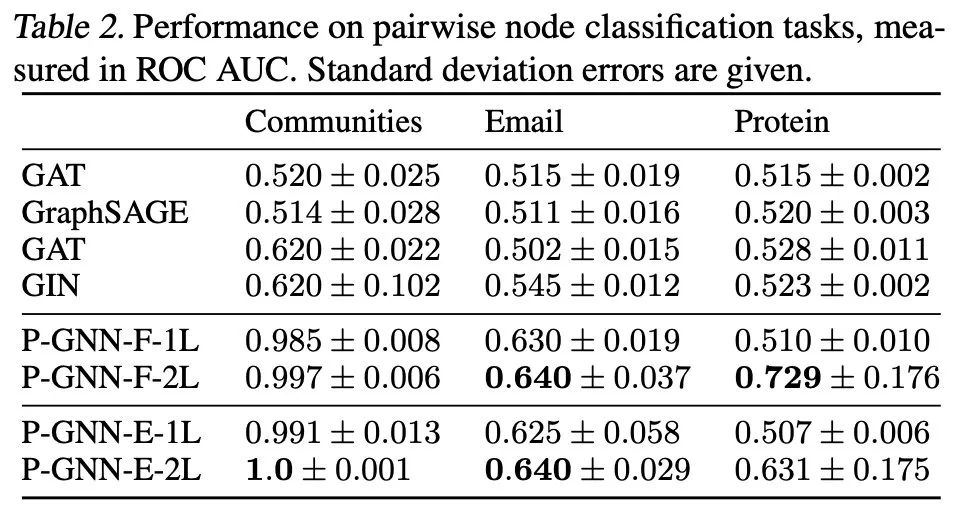
实验结果

2. 几何图神经网络
题目:GEOM-GCN: GEOMETRIC GRAPH CONVOLUTIONAL NETWORKS
作者观察到基于消息传递的GNN存在丢失结构信息和缺乏在不确定性图上学习远程依赖的能力。提出了几何聚合模式来克服这两个缺点。
确定性图:图中的相似节点更可能互相接近,相近的接节点更可能相似。如论文引用网络。
不确定性图:相似的节点在结构上高度相似,但互相距离很远。
如下图左图所示,如果每个节点的都有相同的feature,消息传递GNN区分不开两个处于不同结构里的节点:
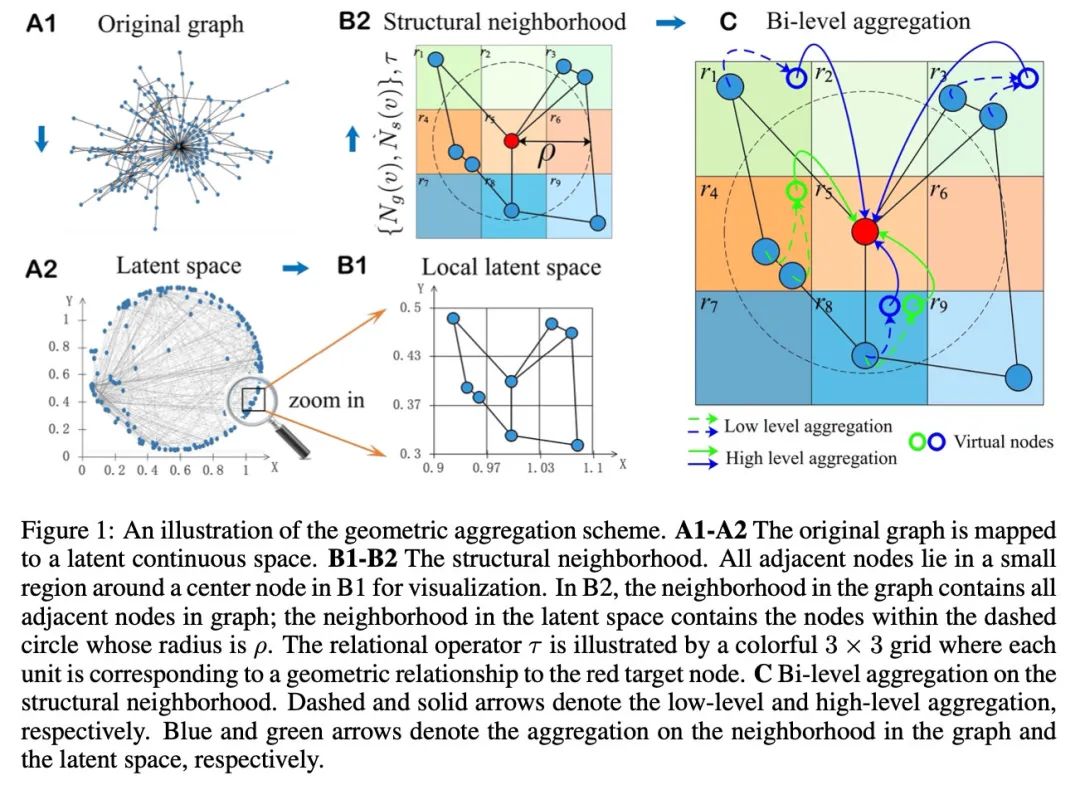
GEOM-GCN构造了隐空间,在隐空间中构建了节点间的近邻关系,同时聚合隐空间的近邻关系和原图上的近邻关系信息。GEOM-GCN利用了节点在隐空间里的相对位置关系,可以区分这两个节点(如右图所示)。
整体流程如下:
(1)用于构造隐空间(latent space)的节点Embedding表示,把节点映射到latent space里:如Isomap、Poincare embedding、struc2vec等可以保留图上的拓扑模式的方法,得到节点在隐空间的表示。
(2)利用隐空间里的距离构造近邻关系,记为s。论文中使用的是欧式距离。
(3)再加上图结构的近邻关系g,有两个近邻关系(g,s)
(4)Bi-level聚合:在两个近邻关系里分别聚合,聚合到虚拟节点上,然后再把虚拟节点上的信息做聚合得到节点的Embedding表示。
Bi-level聚合的细节:
把两个近邻关系聚合到虚拟节点上:节点在第层输出的虚拟节点为
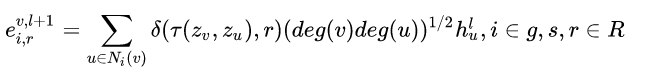
其中,deg(v)表示节点在图中的度,delta是示性函数:第一个参数与第二个参数相等时为1,否则为0;函数是几何操作函数,用于描述两个节点的相对位置,是保留几何空间里位置关系的关键:

表示两个节点的相对位置关系,取值空间是{upper left, upper right, lower left, lower right}。
主要实验结果
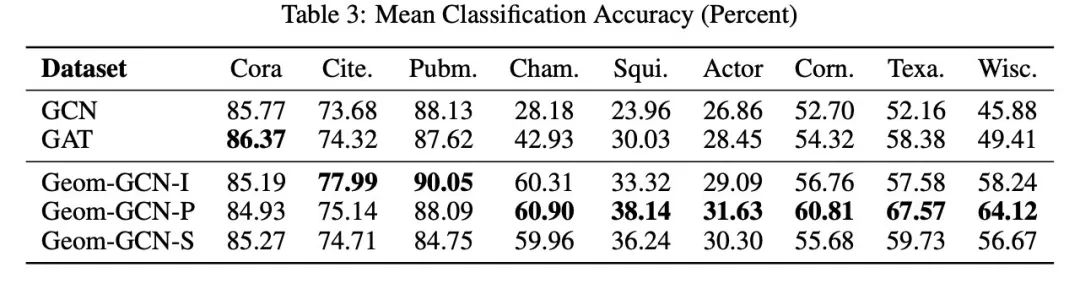
另外,作者使用邻居节点的label的相同比例来度量同质性(下表中的beta),发现在同质性较低的网络上,GEOM-GCN的提升效果更明显。
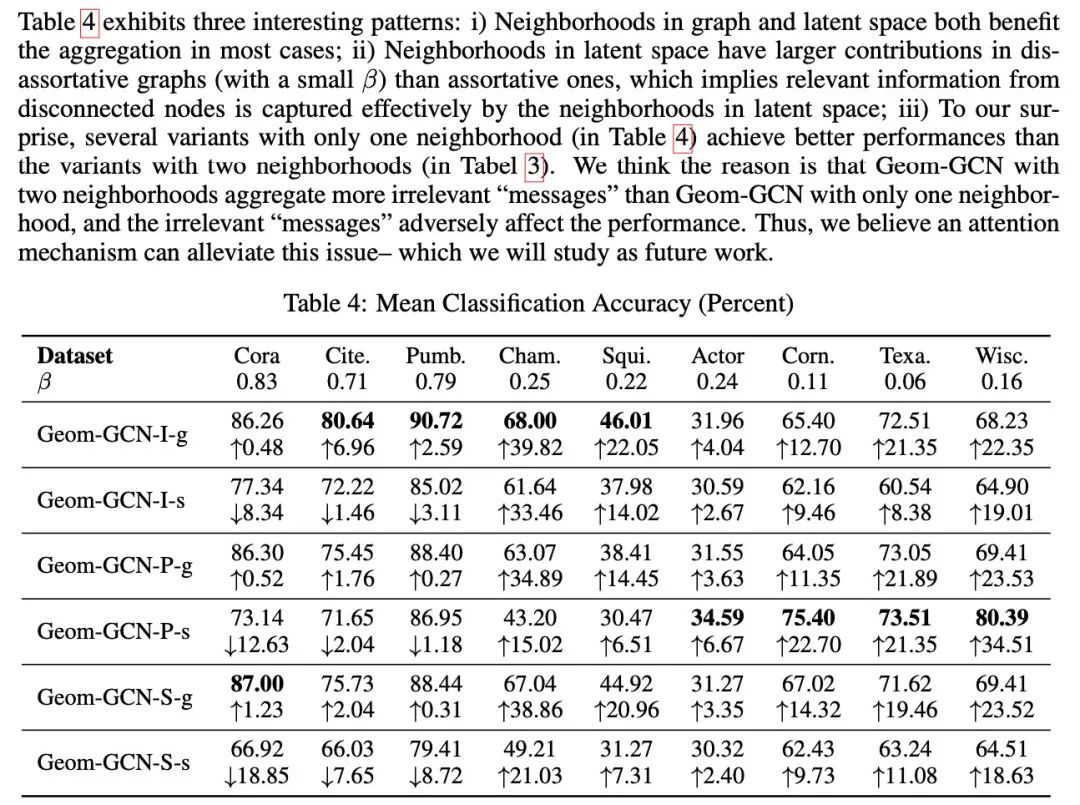

3. 身份感知图神经网络
题目:ID-GNN: Identity-aware Graph Neural Networks
作者发现基于消息传递的GNN表达力的上界是1-WL图同构测试,不能预测节点的聚类系数、最短路径距离,无法区分不同的d-regular graphs(图中的各个节点的度都是d)。作者提出了ID-GNN,表达力可以超越1-WL图同构测试。在计算节点的embeding时,抽取节点的自我中心网络,在计算消息函数时使用异构的消息函数,中心节点和周围节点使用不同的消息函数。
ID-GNN的整体流程如下:
(1)对于要计算embedding的节点v,抽取以它为中心的K-阶自我中心网络;
(2)对于K-阶自我中心网络中的节点u,利用其邻居节点进行消息聚合计算,在聚合中心节点v时,使用不同的消息函数;
(3)重复(2)步骤K次;
(4)得到中心节点v的 Embedding。

ID-GNN的核心点就是计算节点的Embedding时,针对中心节点和周围节点使用不同的消息函数。
ID-GNN-Fast

主要实验结果
作者在模拟数据集和真实数据集上与GNN做了对比实验。
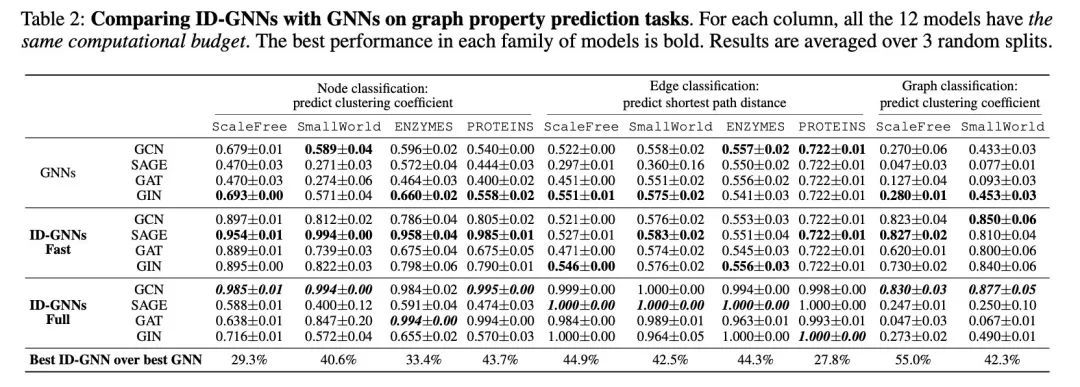
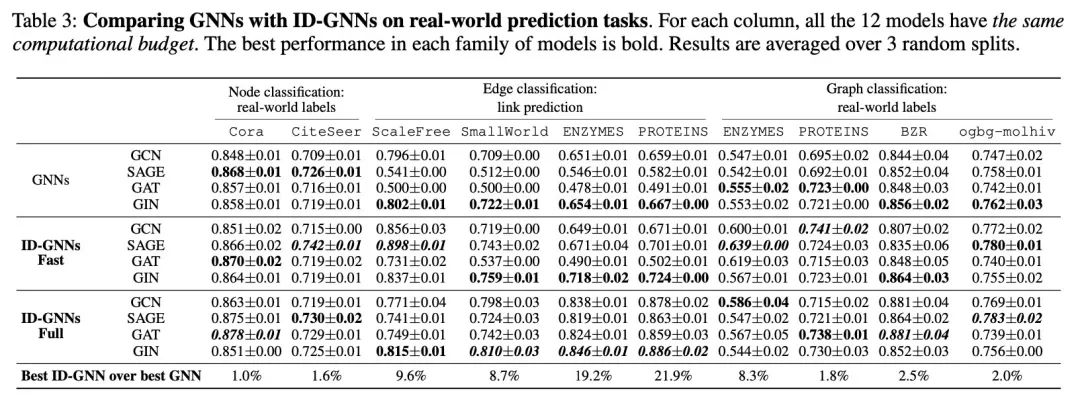
与其他比常见GNN表达力更强的算法的对比,如上文中的P-GNN。
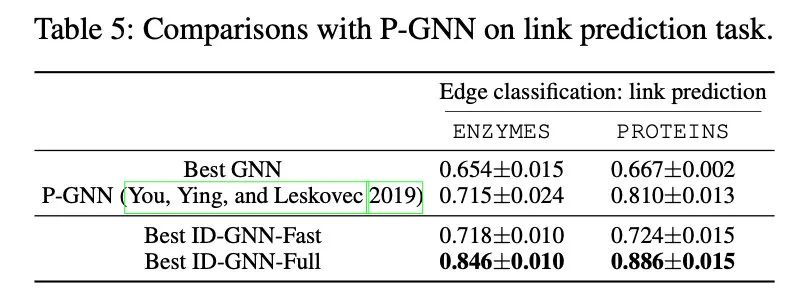
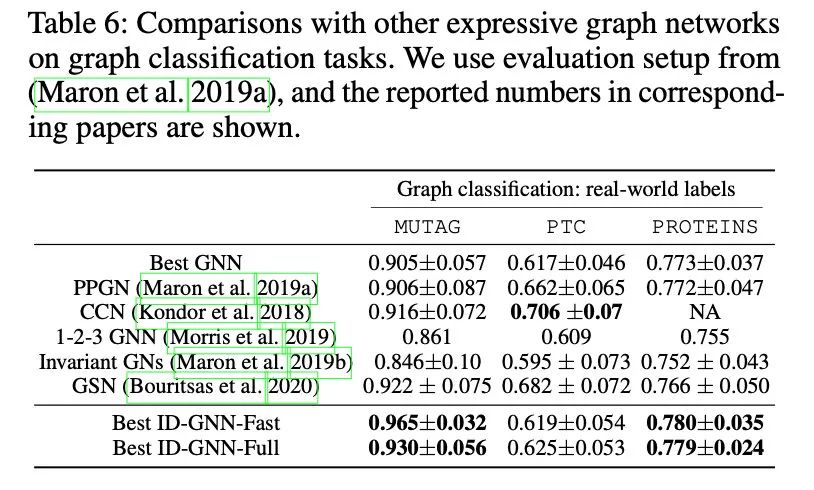
参考资料
[1] Xu, K., Hu, W., Leskovec, J., and Jegelka, S. How powerful are graph neural networks? International Conference on Learning Representations, 2019.
[2] You, J.; Ying, R.; and Leskovec, J. Position-aware graph neural networks. International Conference on Machine Learning (ICML) , 2019. [3] Pei, H., Wei, B., Chang, K. C.-C., Lei, Y., and Yang, B. Geom-gcn: Geometric graph convolutional networks. In ICLR, 2020.
[4] Jiaxuan You, Jonathan Gomes-Selman, Rex Ying, and Jure Leskovec. IdentityAware Graph Neural Networks. In AAAI, 2021.
往期推荐







