


点击上方 蓝字关注我们
ADAPTIVE UNIVERSAL GENERALIZED PAGERANK GRAPH NEURAL NETWORK
https://arxiv.org/pdf/2006.07988.pdf

导读:本文针对GNN存在的两个问题:(1)只适用于homophilic graph;(2)Over-smoothing,提出了一种Generalized PageRank(GPR)GNN架构来解决这些问题,该架构可以自适应地学习GPR权重,从而共同优化节点特征和拓扑信息提取。

1. 问题和动机
大部分现有GNN根本上的缺陷:
1)无法应用于heterophilic graph data上:在[1],[2]中均显示了传统GNN标准模型如GCN, GAT等只适用于homophilic graph data,也就是要求node label相同的点有较多的edge. APPNP 的作者于[3]中也提到,其模型只适用于homophilic graph data. 然而,实际应用中也有许多非homophilic graph data (我们也称作heterophilic graph data),例如在约会社群网络中,异性之间较容易产生连结。因此,一个好的GNN模型应具有universality,也就是可以应用于homophilic 和 heterophilic graph data.
2)存在Over-smoothing问题: 现有的GNN模型大部分都无法如CNN般任意增加层数以增加model complexity. 虽然理论上GNN模型如GCN可以堆任意多层GCN-layer,研究者们发现实际上性能表现会在2-4层时达到最佳,堆栈更多GCN层数反而会使表现严重下滑。而目前对于这一现象一个被大家所接受的说法便是feature over-smoothing. 简单来说,每多一层GCN layer 就相当于让node features在图上做一步random walk,在适当合理的条件下此random walk 会指数收敛到与初始node features 独立的stationary points (只和图结构有关)。[4] 对此一现象的线性情况做了分析,而[5]的分析则包含了非线性的情况。

2. GPR-GNN
在本篇论文中,我们结合了Generalized PageRank 与GNN,同时从理论上解决了上述的两个缺陷。另外,我们提出的GPR-GNN还同时具有可解释性。我们除了在benchmark dataset上展示了GPR-GNN在homophily 和 heterophily 情况下的优越性能,我们也利用cSBM [6]提出了新的synthetic dataset。cSBM能够让我们平滑的控制node features 与 graph topology中关于node label的信息含量,藉此严谨的测试各种GNN模型在各种graph data上的表现。
关于GPR:请见我们2019年NeurIPS论文[7]。其重点在于长距离的propagation/random walk对于node clustering依然具有帮助,且应考虑所有步数的random walk。
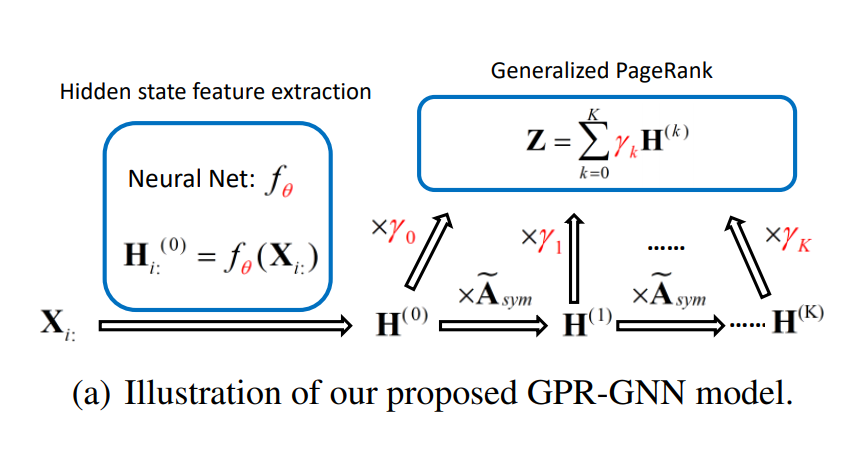
GPR-GNN的模型架构:见Fig1 (a)。其重点在于GPR参数 与神经网络参数是一起同步学习优化的。虽然从解释的角度神经网络于GPRGNN模型中是担任node feature transformation的作用而GPR参数则是学习图拓谱相关信息,但两者可由梯度back propagation来分享node features和图拓谱的信息,这也是为何同步学习GPR参数gamma与神经网络参数theta在GPRGNN中很重要的原因。
GPR-GNN具有universality:我们发现在数学上,GPR与polynomial graph filtering是等价的,其中GPR参数gamma则对应到图滤波器的参数(p3)
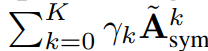
而从传统DSP与GSP可知,多项式滤波器可以近似任意种类的滤波器,包含高通(high-pass, 对应heterophily)与低通(low-pass,对应homophily),因此GPR-GNN确实是universal。另外,从多项式图滤波器的观点来看,的确增加多项式的项数K可以增进其近似最佳图滤波器的能力,这一发现也与我们GPR论文中长距离random walk对node clustering有帮助吻合[7]。在本篇论文中,我们证明了若所有GPR参数皆为非负,和为一,且至少有一非0步数的GPR参数为正,则其对应的图滤波器为低通。这个情形包含了SGC与APPNP,因此这两者皆不具有universality。另外,我们给出了一个高通滤波器的例子,其中GPR参数有负数存在,这一现象与我们的实验吻合(见论文中Fig 1 (b) (c)与实验部分 )
GPR-GNN可避免over-smoothing:我们于Theorem 4.2 证明了GPR-GNN可避免over-smoothing。其核心思路为若某长步数propagation结果并无帮助(使loss增加),则其对应的GPR参数的绝对大小应递减(由gradient based optimizer达成)。

3. 实验部分
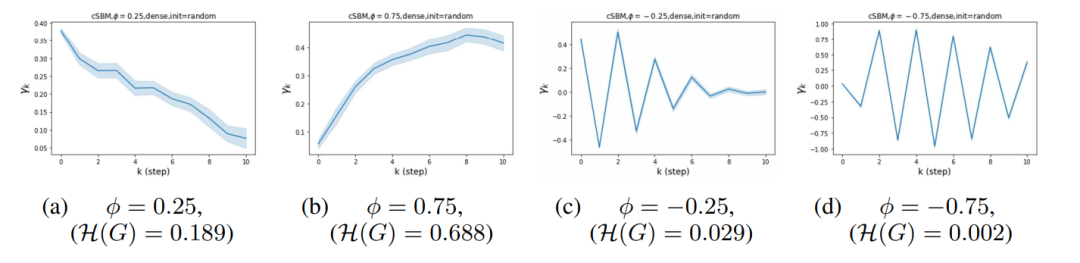
a)synthetic dataset: cSBM. 这是一个random graph的模型,图的部分生成机制为SBM,而node features则为高斯随机向量。在本论文中我们考虑仅有两个cluster (两种label)的情形。在cSBM中参数μ为高斯随机向量的mean,依照label分别为μ,-μ。而 λ 则控制同label的边与不同label的边的密度差。我们令参数ϕ为(粗略地说) λ与μ的比值。ϕ的正负号分别代表homophily 和heterophily,而其绝对值大小(在0,1之间)代表图拓谱与node features所含node label之信息比例,若ϕ=1,-1则node features与node label独立,反之若ϕ=0 则图拓谱与node label独立。从 Figure 2我们可以看出,
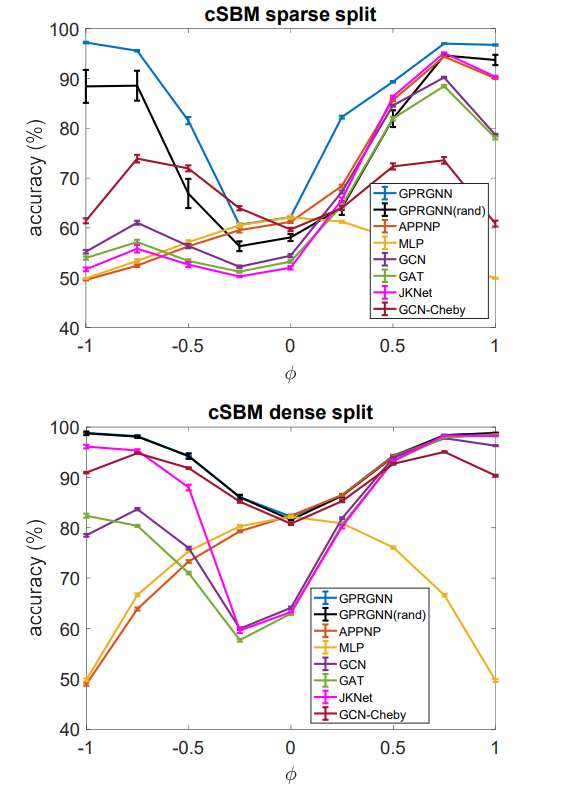
大多数GNN于ϕ>0 (homophily case)有良好表现,但在ϕ<0时只有少数GNN不受影响。特别的是,许多热门GNN模型如GCN,GAT,JKNET等在ϕ=-0.25,0时表现甚至远差于不利用图信息的MLP,这一结果显示这些模型皆bias toward homophily case。当graph data并非strong homophily时这些GNN反而会被图拓谱信息弱化表现。而我们提出的GPR-GNN则是在所有情况中都有最佳表现。此一现象也说明了GPR-GNN的确具有universality。
b)real dataset: 我们测试了5个homophily dataset与5个heterophily dataset。结果列于Table 2。可以看到在homophily dataset中GPR-GNN至少不差于SOTA GNN模型,而在heterophily dataset中相比SOTA有了明显的提升。
c)GPR-GNN的可解释性:我们检视了GPR-GNN在这些dataset中所学习到的GPR 参数(Figure 3, Figure 4 (a)-(d)),可以看出在homophily dataset上所学习到的GPR参数的确皆为非负,而在heterophily dataset上学习到的GPR参数皆有负数,这个结果与我们的理论(Theorem 4.1)吻合。而在实际应用中,我们也可以藉由检测所学习到的GPR参数来更加了解未知graph dataset的特性,这也说明了GPR-GNN的可解释性。
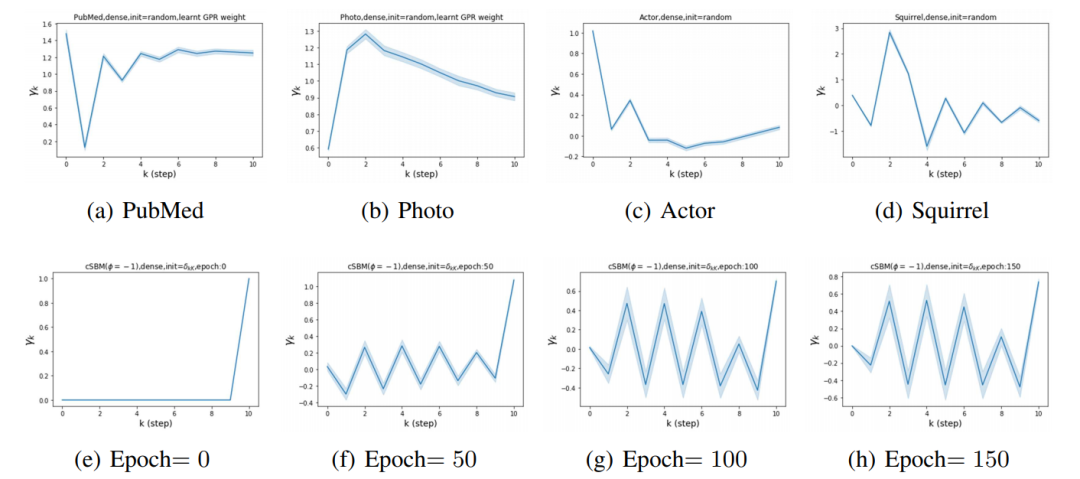
d)GPR-GNN可避免over-smoothing:在最后一组实验中,我们设定GPR参数初始化为只有最后一步有值。在训练之前(epoch 0),我们发现96/100次实验中GPR-GNN的确产生了over-smoothing现象,而在训练完成后,GPR-GNN的准确度从50% (全猜同一label, over-smoothing)提高到了98.8%,检视GPR参数的学习过程也可以看出的确最后一步的GPR 参数的绝对大小有所下降( Figure 4, (e)-(h))。因此,我们从此实验验证了我们的理论Theorem 4.2,显示出GPR-GNN的确可避免over-smoothing。

4. References
[1] Hongbin Pei, Bingzhe Wei, Kevin Chen-Chuan Chang, Yu Lei, and Bo Yang. Geom-gcn: Geometricgraph convolutional networks. InInternational Conference on Learning Representations, 2019.
[2] Jiong Zhu, Yujun Yan, Lingxiao Zhao, Mark Heimann, Leman Akoglu, and Danai Koutra. General-izing graph neural networks beyond homophily.arXiv preprint arXiv:2006.11468, 2020.
[3] Aleksandar Bojchevski, Johannes Klicpera, Bryan Perozzi, Amol Kapoor, Martin Blais, BenedekR ́ozemberczki, Michal Lukasik, and Stephan G ̈unnemann. Scaling graph neural networks withapproximate pagerank. InProceedings of the 26th ACM SIGKDD International Conference onKnowledge Discovery & Data Mining, pp. 2464–2473, 2020
[4] Qimai Li, Zhichao Han, and Xiao-Ming Wu. Deeper insights into graph convolutional networks forsemi-supervised learning. InThirty-Second AAAI Conference on Artificial Intelligence, 2018.
[5] Kenta Oono and Taiji Suzuki. Graph neural networks exponentially lose expressive power for nodeclassification. InInternational Conference on Learning Representations, 2020
[6] Yash Deshpande, Subhabrata Sen, Andrea Montanari, and Elchanan Mossel. Contextual stochasticblock models. InAdvances in Neural Information Processing Systems, pp. 8581–8593, 2018
[7] Pan Li, I Chien, and Olgica Milenkovic. Optimizing generalized pagerank methods for seed-expansion community detection. InAdvances in Neural Information Processing Systems, pp.11705–11716, 2019.







