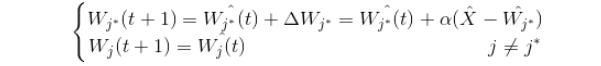SOM（Self-organizing Maps）自组织映射是一种人工神经网络（ANN），由芬兰赫尔辛基大学教授Teuvo Kohonen于1981年提出，因此又称为Kohonen算法。SOM自组织映射算法是一种聚类和高维可视化的无监督学习算法，是通过模拟人脑对信号处理的特点而发展起来的一种人工神经网络。竞争学习规则的生理学基础是神经细胞的侧抑制现象：当一个神经细胞兴奋后，会对其周围的神经细胞产生抑制作用。最强的抑制作用是竞争获胜，这种做法称为“胜者为王”（WTA）。（正文部分资料来源于网络）
1.介绍
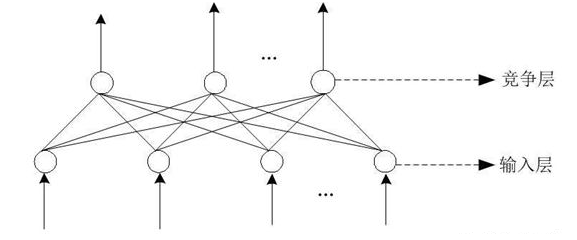
SOM算法是无导师学习网络，SOM模型本质上是一种只有输入层--隐藏层的神经网络，它通过自动寻找样本中的内在规律和本质属性，自组织，自适应地改变网络参数与结构。SOM 也是一种降维算法，用于生成训练样本的低维空间，可以将高维数据间复杂的非线性统计关系转化为简单的几何关系，以低维的方式呈现出来，实现高维数据可视化，然后根据降维之后的数据再进行聚类。
在聚类问题中，你需要一个神经网络来根据相似性对数据进行分组。其主要应用于语音识别、图像处理、分类聚类、组合优化、数据分析和预测等领域，具体的还有，例如：根据人们的购买模式进行市场细分；数据挖掘可以通过将数据划分为相关子集来完成；或者生物信息学分析，比如用相关的表达模式对基因进行分组。在汽车领域也有很多应用，比如汽轮发电机多故障诊断的SOM神经网络方法，基于SOM神经网络的柴油机故障诊断等。
2.工作原理
隐藏层中的一个节点代表一个需要聚成的类。训练时采用“竞争学习”的方式，每个输入的样例在隐藏层中找到一个和它最匹配的节点，称为它的激活节点，也叫“winning neuron”，紧接着更新激活节点的参数。同时，和激活节点临近的点也根据它们距离激活节点的远近而适当地更新参数。
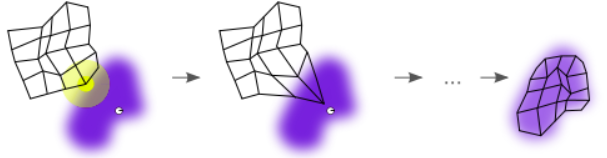
其训练过程是用下面的例子表示，其中紫色区域表示训练数据的分布状况，白色网格表示从该分布中提取的当前训练数据。开始，SOM 节点位于数据空间的任意位置，这个可以随机给出。开始学习时，最接近训练数据的节点（黄色高亮部分）会被选中，同时它和网格中的邻近节点一样，朝训练数据移动。在多次迭代之后，网格倾向于最右图中近似该种数据分布。
其随机数据和训练数据的映射过程是将训练数据输入到网络中时，计算出各个训练数据和随机数据的权重向量的欧几里距离。权重向量与输入最相似的神经元称为最佳匹配单元（BMU）。BMU 的权重和 SOM 网格中靠近它的神经元会朝着输入矢量的方向调整。
3.算法流程
1）向量归一化
对SOM网络中的当前输入模式向量、竞争层中各神经元对应的权向量，全部进行归一化处理。
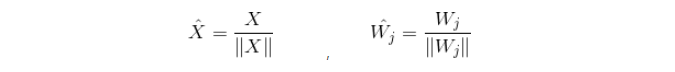
2）寻找获胜神经元
即每个输入的数据找到其最匹配的节点。将归一化X与竞争层所有神经元对应的的归一化权向量Wj(j=1,2,3,4,5...m)进行相似性比较。最相似的神经元获胜。
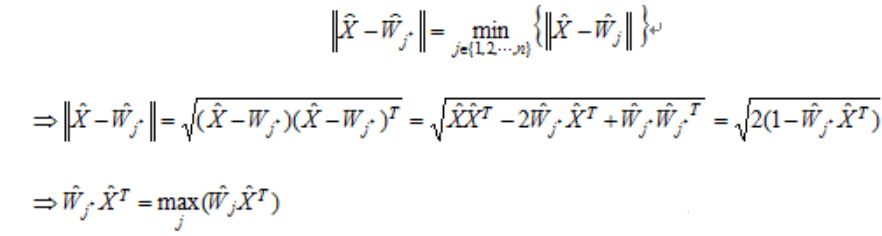
3）网络输出与权调整
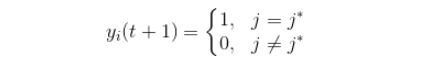
获胜神经元才调整其权向量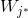
，其他不做改变，其权向量学习调整如下：
α为学习率，0<α≤1，α一般随着学习的迭代而减小，调整的幅度越来越小，根据距离更新强度打折扣，趋于聚类中心。
4）重新归一化处理
归一化后的权向量经过调整后，得到的新向量不再是单位向量，因此要对学习调整后的向量重新归一化，循环运算，直到学习率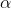
衰减到0.
4.优缺点
SOM算法优点：
1）将相邻关系强加在簇质心上，有利于聚类结果的解释；
2）具有降维功能；
3）可视化；
4）自组织；
5）无导师学习；
6）拓扑结构保持；
7）概率分布保持。
SOM算法缺点：
1) 用户必选选择参数、邻域函数、网格类型和质心个数；
2) 一个SOM簇通常并不对应单个自然簇、可能有自然簇的合并和分裂；
3) 缺乏具体的目标函数；
4) SOM不保证收敛。
5.案例
对鸢尾花进行聚类，尝试构建一个将鸢尾花聚类成多个自然类的神经网络，以使相似的类分组在一起。每朵鸢尾花都用四个特征进行描述：.
萼片长度 (cm)
萼片宽度 (cm)
花瓣长度 (cm)
花瓣宽度 (cm)
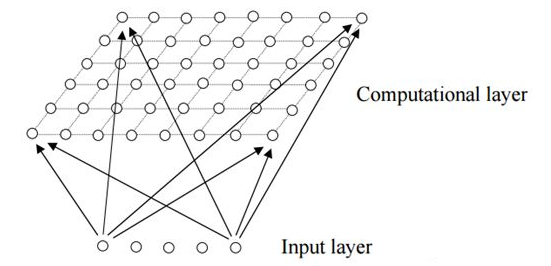
四个花属性将作为 SOM 的输入，SOM 将它们映射到二维神经元层。
1）准备数据
通过将数据组织成输入矩阵 X，为 SOM 设置聚类问题数据。
输入矩阵的每个第 i 列将具有四个元素，表示在一朵花上获取的四个测量值，有150个花的数据就是4*150的矩阵。
2）使用神经网络进行聚类
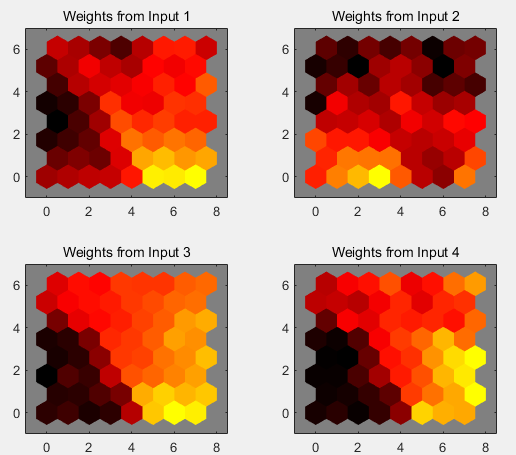
改实验中我们将具有以 8×8 六边形网格排列的 64 个神经元的二维层。通常，使用更多神经元可以获得更多细节，而使用更多维度则可对更复杂特征空间的拓扑进行建模。
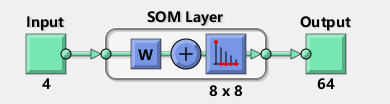
开始训练
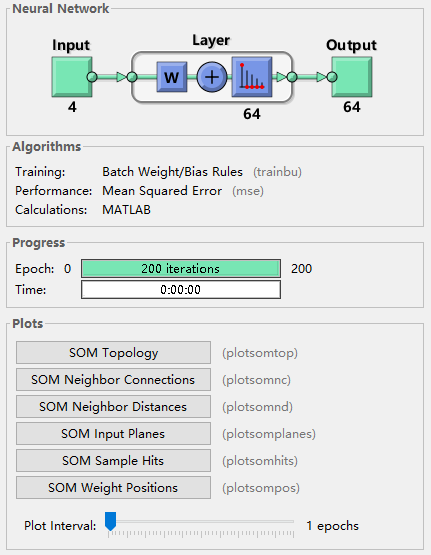
这里使用自组织映射计算每个训练输入的类向量。这些分类涵盖了已知花朵所填充的特征空间，它们现在可用于对新花朵进行相应分类。网络输出将是一个 64×150 矩阵，其中每个第 i 列表示第 i 个输入向量（其第 j 个元素为 1）的第 j 个聚类。
拓扑：64 个神经元的自组织映射拓扑：
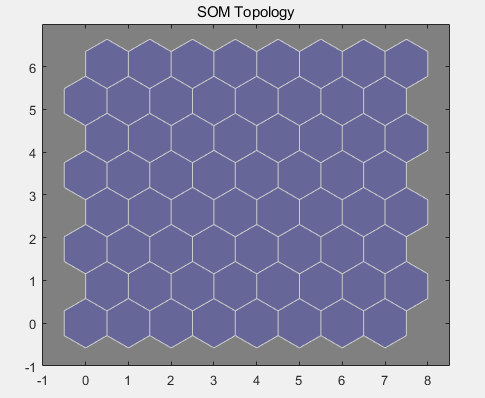
临近连接：神经元邻点连接。邻点通常用于对相似样本进行分类。
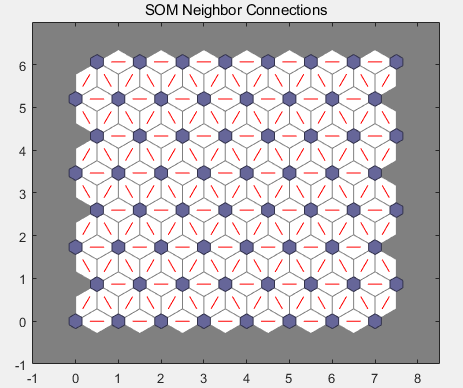
每个类中的花朵数量：具有大量命中的神经元区域所表示的类代表相似的填充度高的特征空间区域，而命中较少的区域表示填充稀疏的特征空间区域。
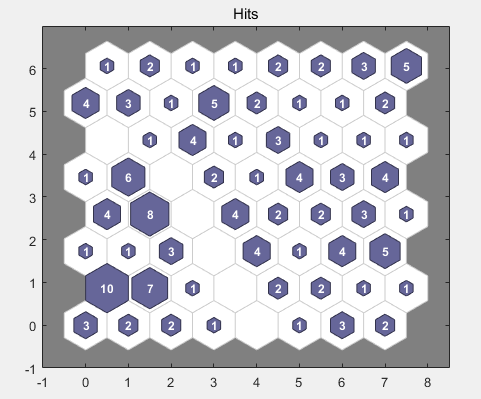
权重距离：显示每个神经元的类与其邻点的距离（以欧几里德距离表示）。浅色连接表示输入空间的高度连接区域。而深色连接表示的类代表相距很远且相互之间很少或没有花朵的特征空间区域。将较大输入空间区域分开的深色连接的长边界表明，边界两侧的类代表特征非常不同的花朵
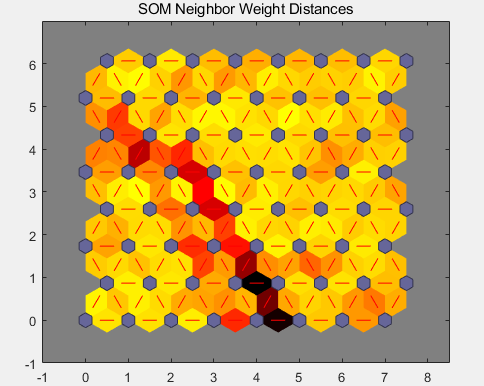
各特征权重平面：显示四个输入特征中每个特征的权重平面。它们是权重的可视化，这些权重将每个输入连接到以 8×8 六边形网格排列的 64 个神经元中的每一个。深色代表较大权重。如果两个输入具有相似的权重平面（它们的颜色梯度可能相同或相反），则表明它们高度相关。
