Table of Contents
- 一. 随机变量的期望
- 1.1 赌金分配
- 1.2 离散型随机变量的期望
- 1.3 (0-1)分布的数学期望
- 1.4 二项分布的数学期望
- 1.5 连续性随机变量的期望
- 1.6 均匀分布的数学期望
- 1.7 正态分布的数学期望
- 1.8 赌 博的公平性
- 1.9 数学期望的性质
- 二. 方差
- 2.1 运动员选拔
- 2.2 随机变量的方差
- 2.3 (0-1)分布的方差
- 2.4 均匀分布的方差
- 2.5 方差的性质
- 2.6 二项分布的方差
- 2.7 正态分布的方差
- 2.8 协方差与相关系数
- 2.9 不相关与相互独立
- 2.10 矩
- 参考:
一. 随机变量的期望
1.1 赌金分配

| 局数 | 胜者 | 最终胜利者 | 概率 |
|---|---|---|---|
| 4 | 甲 | 甲 | 0.5 |
| 4 | 乙 | - | 0.5 |
| 5 | 甲 | 甲 | 0.5*0.5 |
| 5 | 乙 | 乙 | 0.5*0.5 |
甲获胜的概率是 : 0.5+0.25=0.75
乙获胜的概率是: 0.25

1.2 离散型随机变量的期望
离散型随机变量的期望:

运动员选拔:
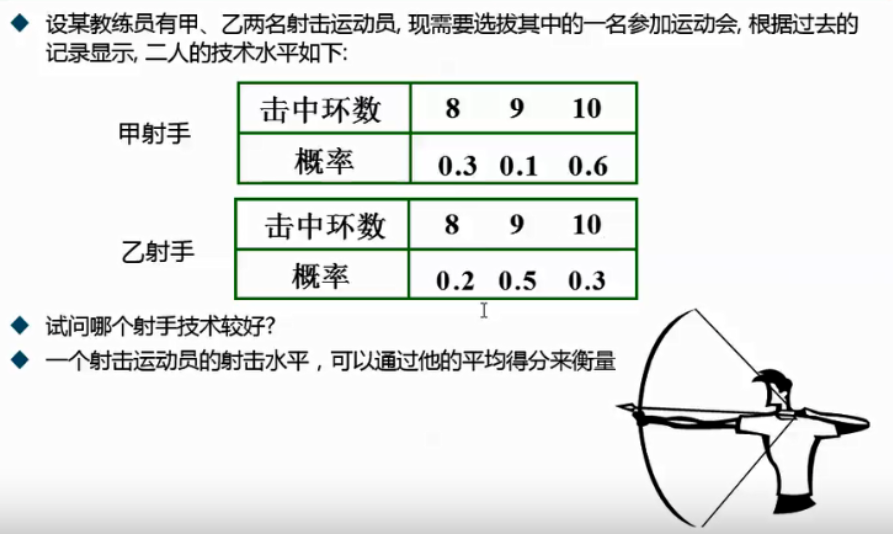

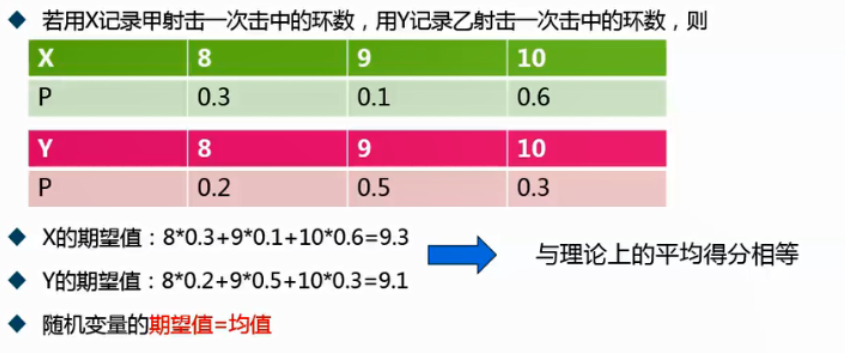
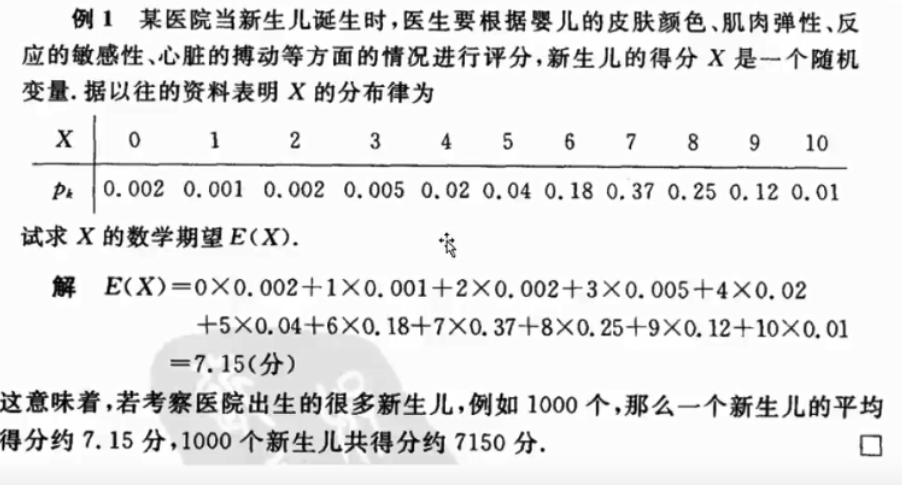
新生婴儿得分:
停车时间:

1.3 (0-1)分布的数学期望

1.4 二项分布的数学期望


1.5 连续性随机变量的期望
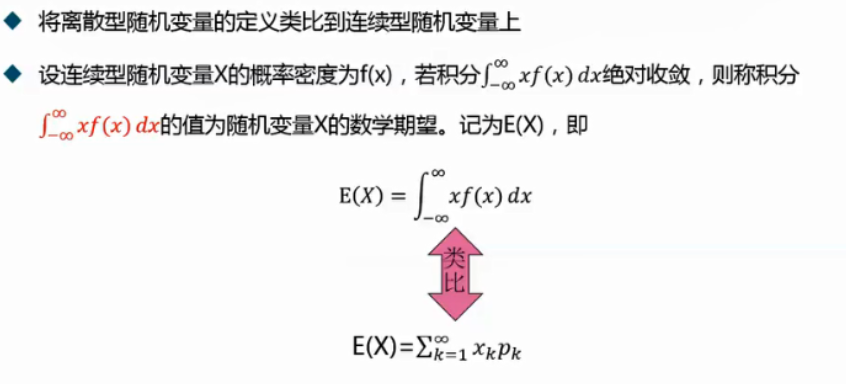
例子:


1.6 均匀分布的数学期望

1.7 正态分布的数学期望

1.8 赌 博的公平性
这个例子其实初看下就觉得不公平,输的概率更大

这个案例最开始觉得,赢的概率更大,算了概率后发现并不是这样的,看来只有错买的,没有错卖的.


1.9 数学期望的性质


二. 方差
2.1 运动员选拔
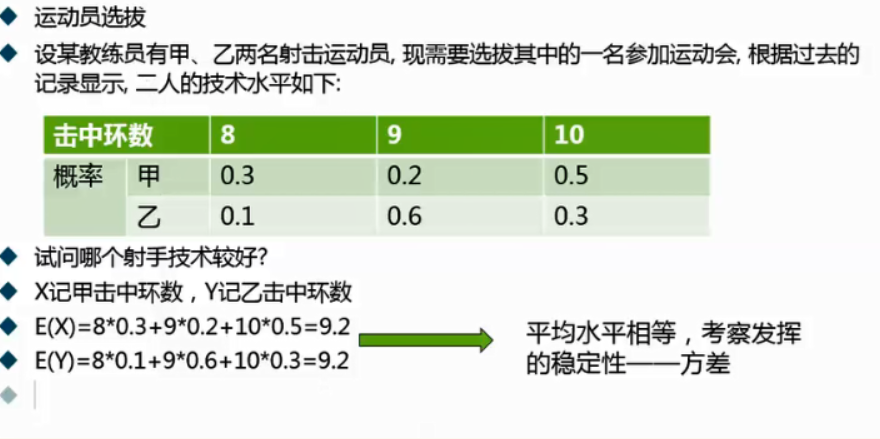
方差表示数据的离散程度.

2.2 随机变量的方差

标准化:
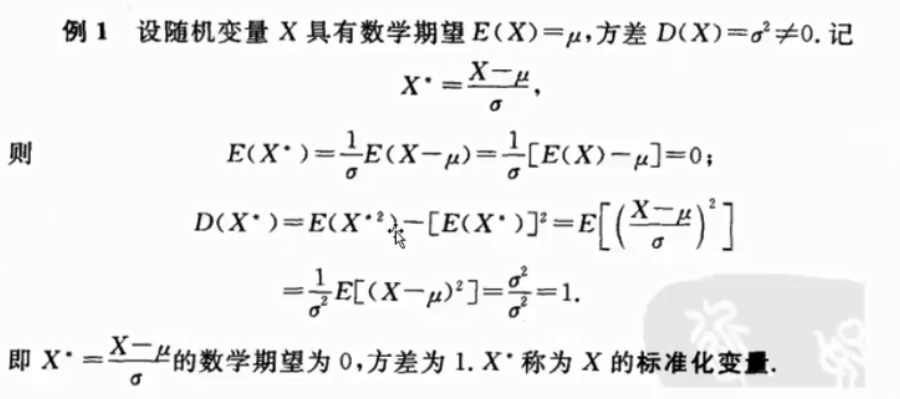
2.3 (0-1)分布的方差
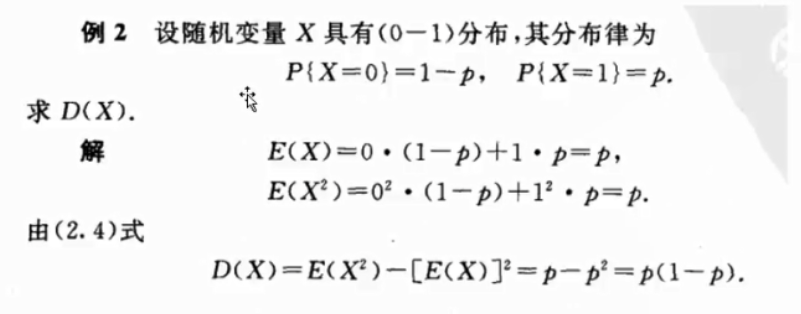
2.4 均匀分布的方差

2.5 方差的性质

2.6 二项分布的方差

2.7 正态分布的方差

这个0.0025是两个相加的来的,那么也就是即便是减法,方差也是相加而不是相减。

2.8 协方差与相关系数
关于协方差与相关系数与相关系数比较好的文章
https://www.zhihu.com/question/20852004

协方差的性质:

相关系数的性质:
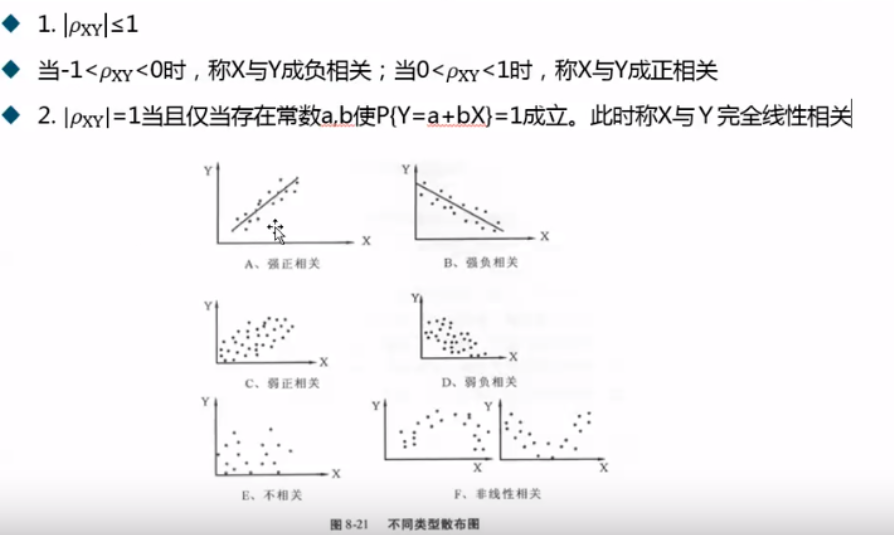
2.9 不相关与相互独立

例:
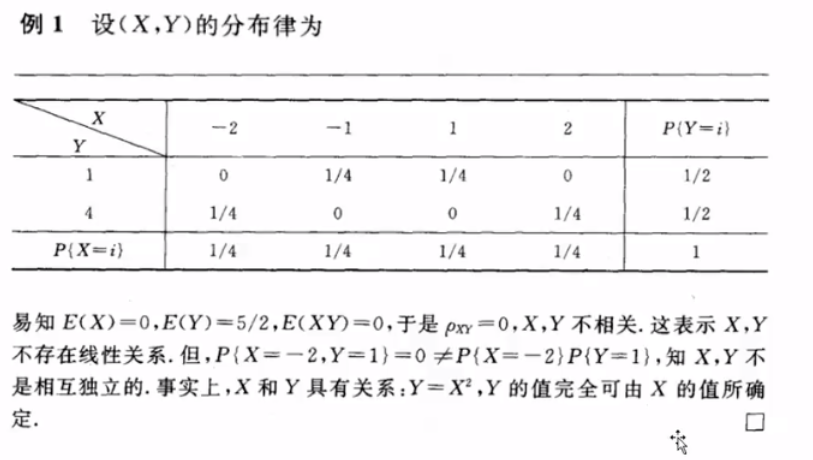
2.10 矩


参考:
- http://www.dataguru.cn/article-4362-1.html
「喜欢这篇文章,您的关注和赞赏是给作者最好的鼓励」
关注作者
【版权声明】本文为墨天轮用户原创内容,转载时必须标注文章的来源(墨天轮),文章链接,文章作者等基本信息,否则作者和墨天轮有权追究责任。如果您发现墨天轮中有涉嫌抄袭或者侵权的内容,欢迎发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






