1、引言
Elasticsearch中的 Terms 桶聚合基于我们的数据动态构建桶;但是它并不知道到底生成了多少桶。大多数时候对单个字段的聚合查询还是非常快的, 但是当需要同时聚合多个字段时,就可能会产生大量的分组,最终结果就是占用 es 大量内存,从而导致 OOM 的情况发生。
在Elasticsearch中,对于具有许多唯一术语和少量所需结果的字段,延迟子聚合的计算直到顶部父级聚合被修剪会更有效。通常,聚合树的所有分支都在一次深度优先传递中展开,然后才会发生任何修剪。在某些情况下,非常浪费资源,并且可能会遇到内存限制。
而本文所讲的内容即通过 DFS 和 BFS 提升检索效率和提升聚合性能,基本原理即:推迟子聚合的计算。
2、案例
假设有索引actor_films
,存储信息为某些演员和其出演过的一些电影。
2.1 假设有如下需求:
统计演员列表中总票房最高的前十位演员每个人票房最高的前五部电影
因为无法导入大量数据,并且聚合代码本身非本文所讲解重点,因此下面代码采用伪代码方式,即跳过具体的逻辑部分。
伪代码如下:
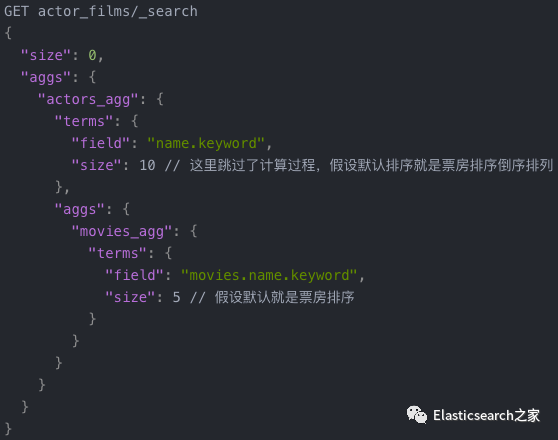
2.3 性能痛点
首先,上述代码描述的问题可用下图表示,假设演员数据有M个,M是一个很大的数值,比如1万、10万或者更多。每位演员出演过N部电影,每个M对应的N可能不同,N 大于5。
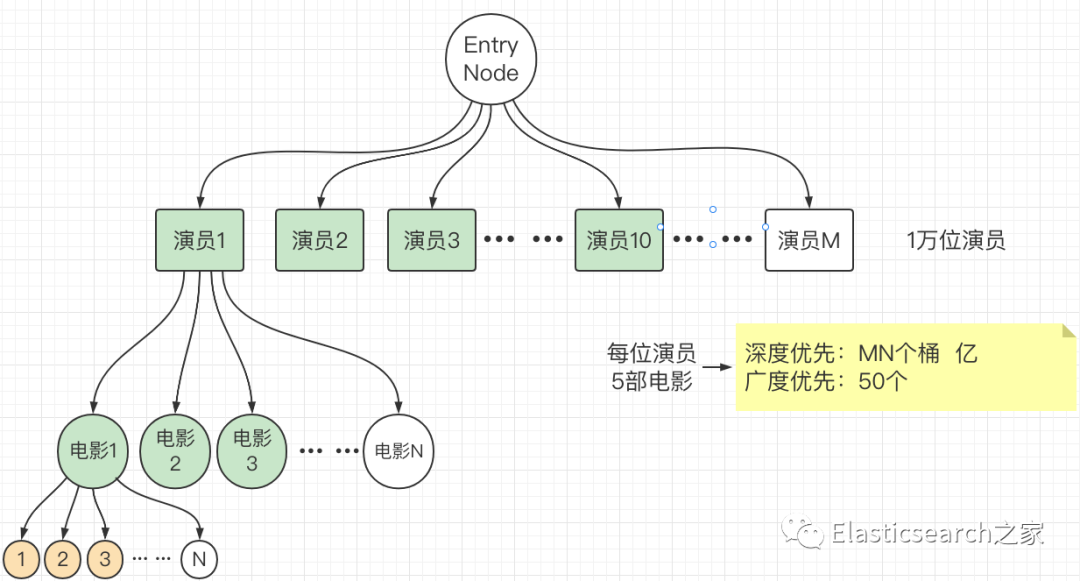
按照上述需求,我们最终要返回的桶数量最大值为 50。默认情况下,ES 会先构建完整的树,然后修剪无用节点。下图中表示即先遍历 演员1,然后遍历演员一的第一个分支,直至第一个分支没有子节点,回溯至演员一的第二个分支,直至遍历完演员1 的所有分支,回溯至Entry,然后遍历演员2。最终遍历节点数为 MN。如果演员数量有1万,平均每个演员10部电影,此时遍历所产生的的计算为10万次,而我们真正需要的只有50次!
3 解决方式
3.1 Collect mode
ES 中允许设置参数collect_mode
:
"collect_mode": "{collect_mode.value}"
3.2 参数
•breadth_first:即使用广度优先算法。即:先做第一层聚合,逐层修剪。广度优先仅仅适用于每个组的聚合数量远远小于当前总组数的情况下,因为广度优先会在内存中缓存裁剪后的仅仅需要缓存的每个组的所有数据,以便于它的子聚合分组查询可以复用上级聚合的数据。广度优先的内存使用情况与裁剪后的缓存分组数据量是成线性的。对于很多聚合来说,每个桶内的文档数量是相当大的。•depth_first:使用深度优先算法,即:先构建完整的树,然后修剪无用节点。
3.3 完整代码如下
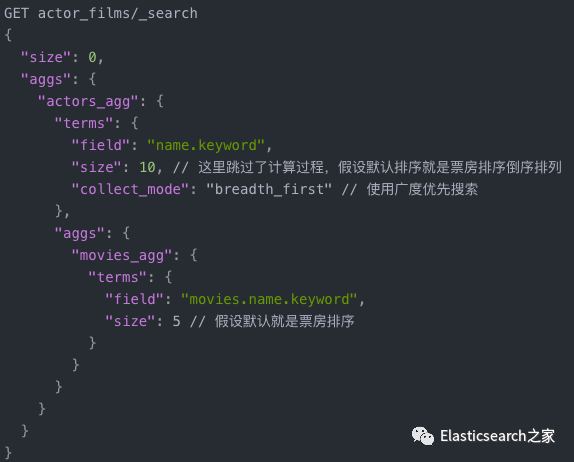
4、深度优先搜索(Depth-First Search)
4.1 什么是深度优先算法
一句话导读:当你玩迷宫游戏的时候,你进入迷宫那一刻,右手摸着墙手不离开,不停前进,直至走出迷宫,此时你使用的就是深度优先搜索。
4.2 图的深度优先搜索
和树
不同,图没有根节点,并且是可以回溯的,比如下图所示,为一个 11 节点的图搜索表示
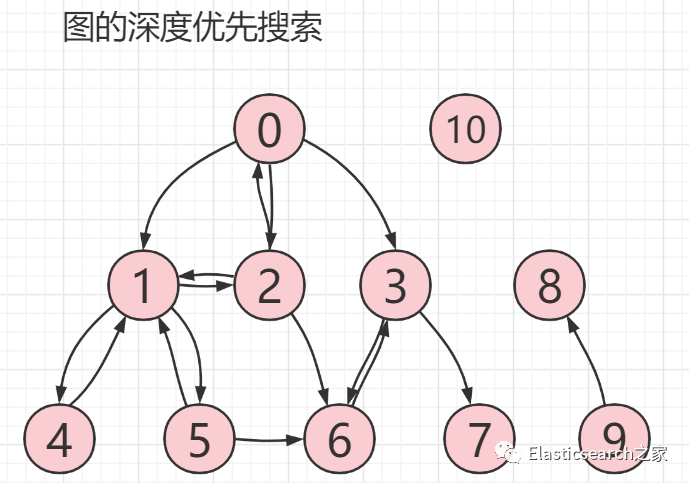
其中:
节点0 :包含三个出度,分别指向其三个邻接点,分别为节点1、节点2、节点3
,同时节点0
也是节点2
的邻接点。节点1:包含三个邻接点,分别为节点2、节点4、节点5
节点2:邻接点为节点0、节点1、节点6
。节点3:邻接点为节点6、节点7
。节点4:邻接点为节点1
。节点5:邻接点为节点1、节点6
。节点6:邻接点为节点3
。节点7:没有任何邻接点,因为节点7
的出度并没有指向任何节点。或者说其没有任何出度节点8:和节点7
一样,没有任何邻接点节点9:邻接点为节点8
。节点10:和节点7
一样,没有任何邻接点。
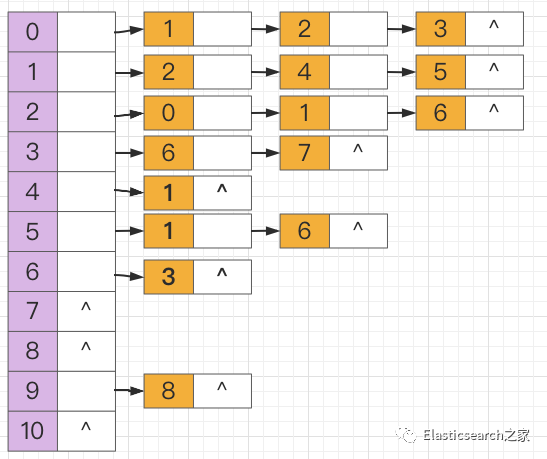
4.3 邻接表
下图为 2.2 中图搜索所示图
的邻接表形式。可以看到,节点7、节点8、节点10
是没有任何出度和邻接点的。
4.4 邻接矩阵
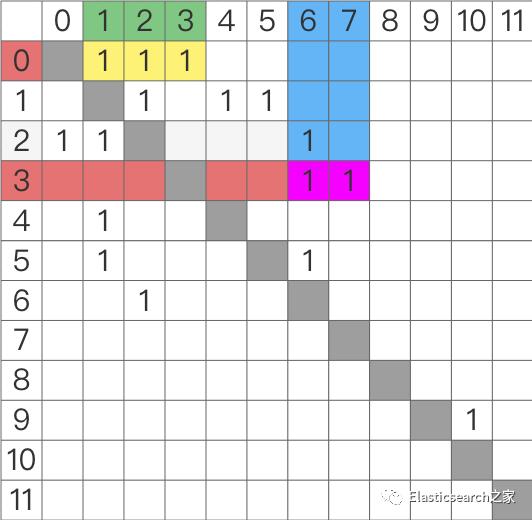
下图为 2.2 中图搜索所示图
的邻接矩阵
表示
其中,纵坐标表示 出度节点,横坐标表示 邻接点
比如,下图中:
•节点0:邻接点为节点1、节点2、节点3
•节点3:邻接点为节点6、节点7
4.5 图的深度优先搜索遍历过程
4.5.1 栈
图的深度优先遍历是靠栈
来完成的,我们首先创建一个空栈

4.5.2 Visited数组

我们借助 Visited数组,来标识当前节点 n 是否被访问过,空值代表 false.
4.5.3 遍历序列
准备一个空的遍历序列,用来存放最终生成的访问元素。

4.5.4 遍历过程
首先,图是没有根节点的,我们可以以任何节点作为其起始节点,下面我就以节点0
为起始节点为例,演示一下图的深度搜索过程。
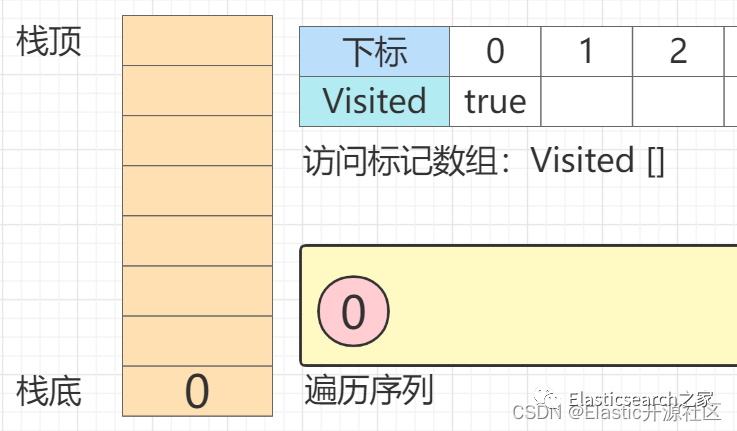
第1步 节点0
入栈
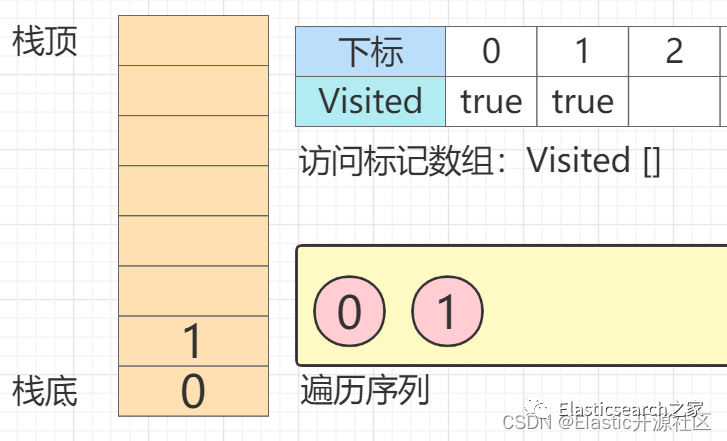
第2步 节点0
的第一个邻接点入栈
第3步 节点1
的第一个邻接点节点2
入栈
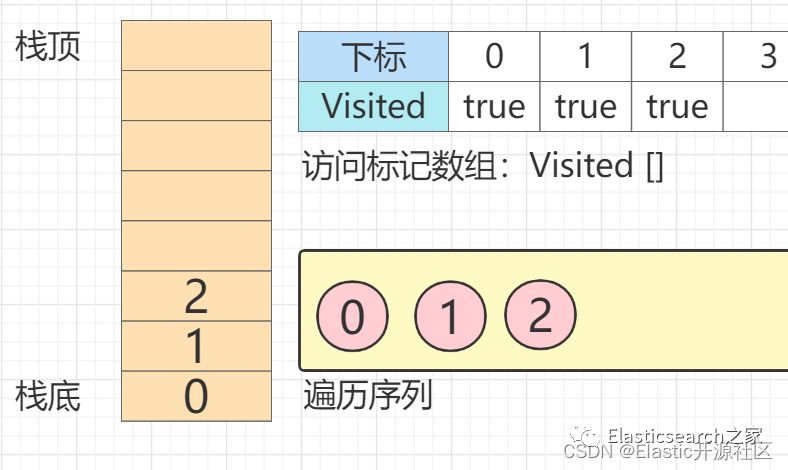
第4步
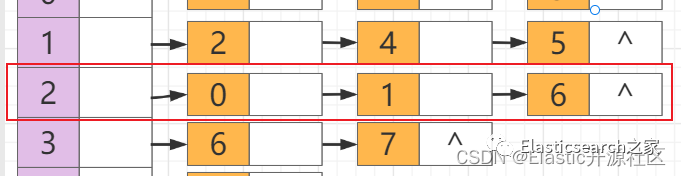
节点2
的第一个邻接点节点0
入栈,但是节点0
visited = true,即已经被访问过,因此顺延节点1
,同样节点1
也被访问过,因此继续顺延至节点6
,节点6
入栈并标记访问
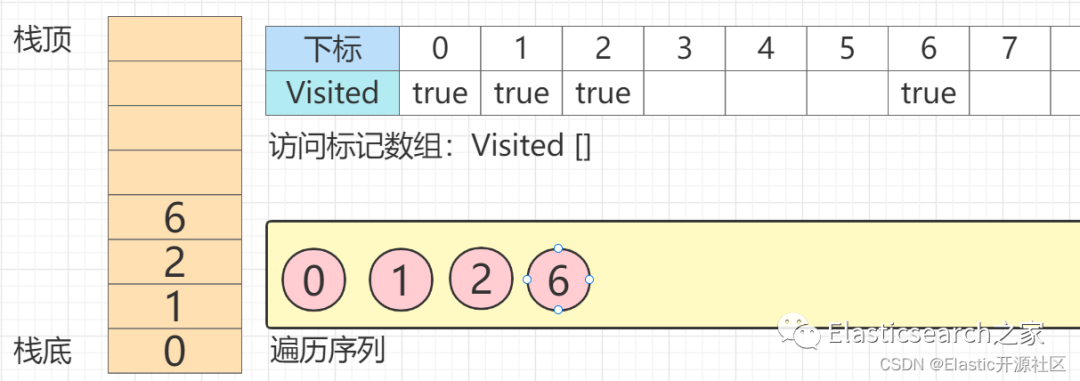
第5步 节点6
的第一个邻接点也是唯一一个邻接点:节点3
入栈
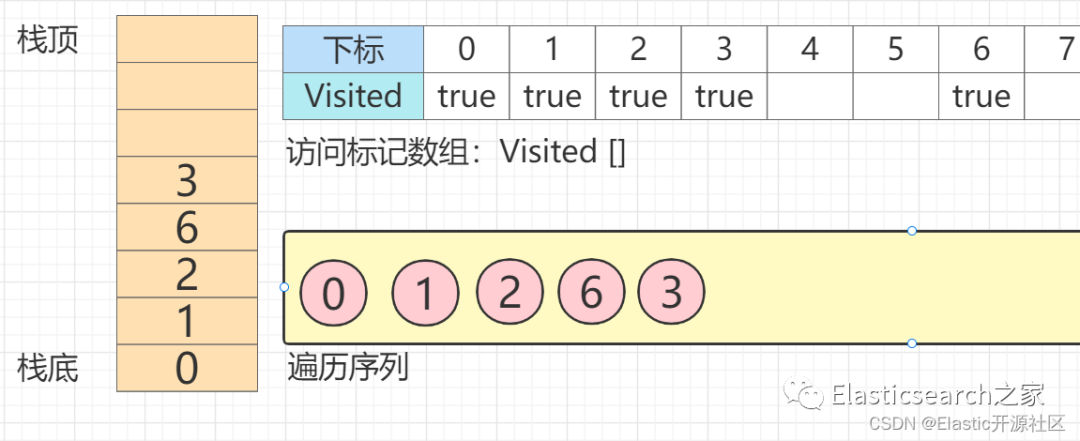
第6步 节点3
的第一个邻接点也是唯一一个邻接点:节点7
入栈
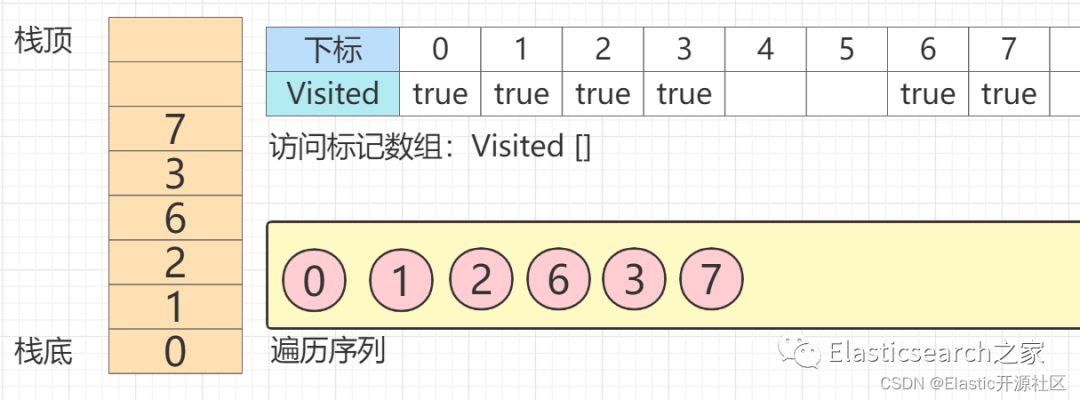
第7步 节点7
没有任何出度和邻接点,此时节点7
出栈,回溯至节点3
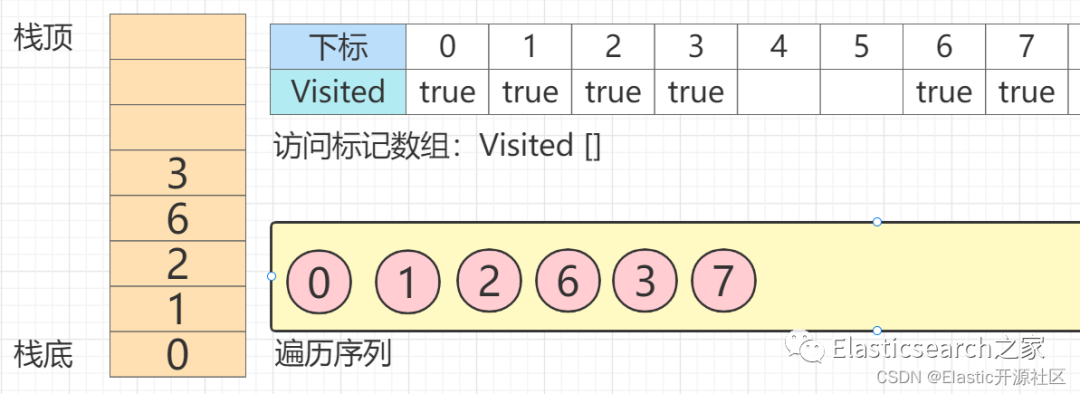
第8步 节点3
的唯一一个邻接点:节点7
已经被访问,此时节点3
的所有邻接节点均已访问,此时,节点3
出栈,回溯至节点6
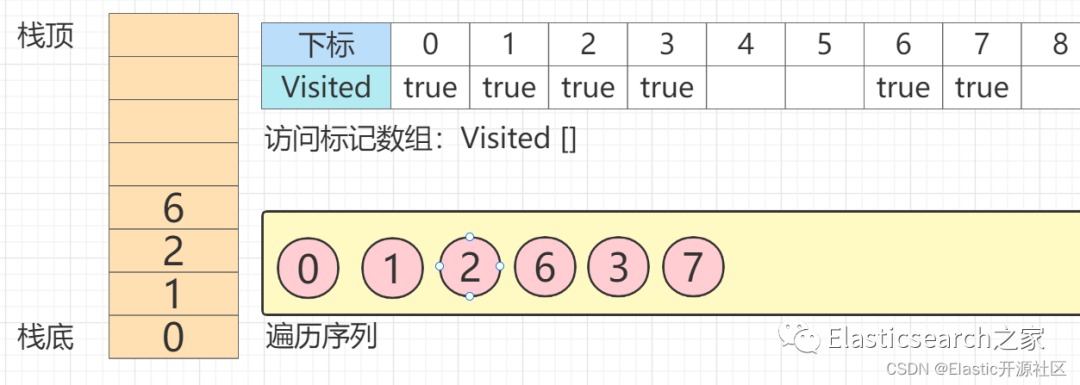
第9步 同理,此时节点6
的唯一一个邻接点:节点3
已经被访问,此时节点6
的所有邻接节点均已访问,此时,节点6
出栈,回溯至节点2
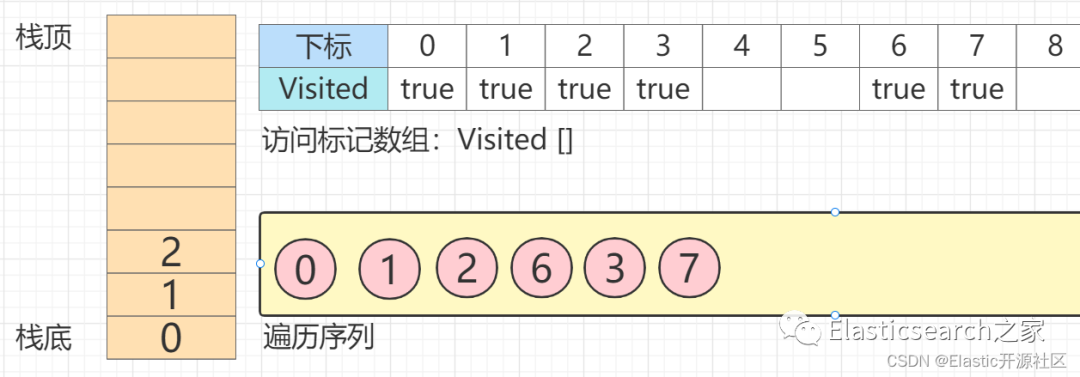
第10步
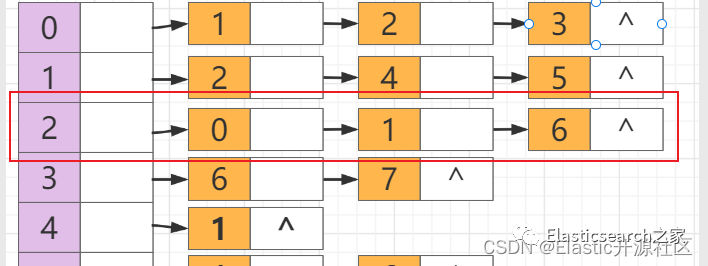
此时节点2
的三个邻接点:节点0、节点1、节点6
均已被访问过,因此节点2
出栈,回溯至节点1
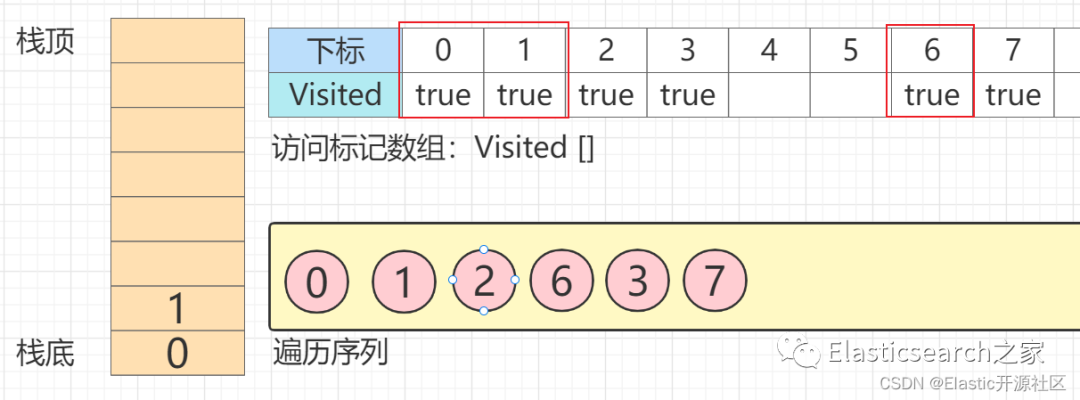
第11步 此时节点1
的三个邻接点:节点2、节点4、节点5
其中节点2
已被访问,因此节点4
入栈
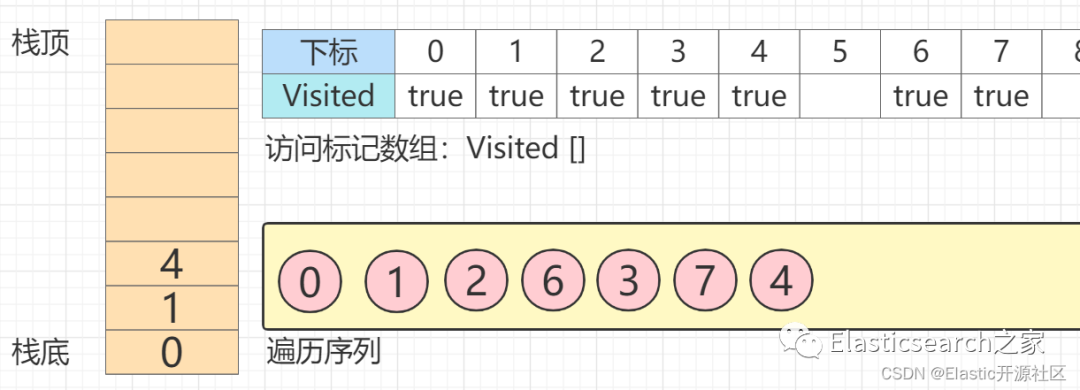
第12步 以此类推,节点4
出栈 => 节点5
入栈,并回溯至节点1
,节点1
所有邻接点均已访问。节点1
出栈,回溯至节点0
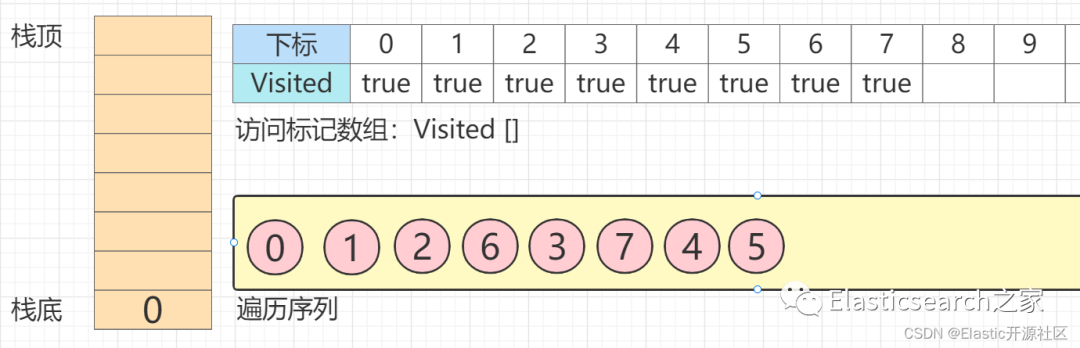
第13步 此时,节点0
的所有出度邻接点均已访问,节点0
出栈,此时为空栈
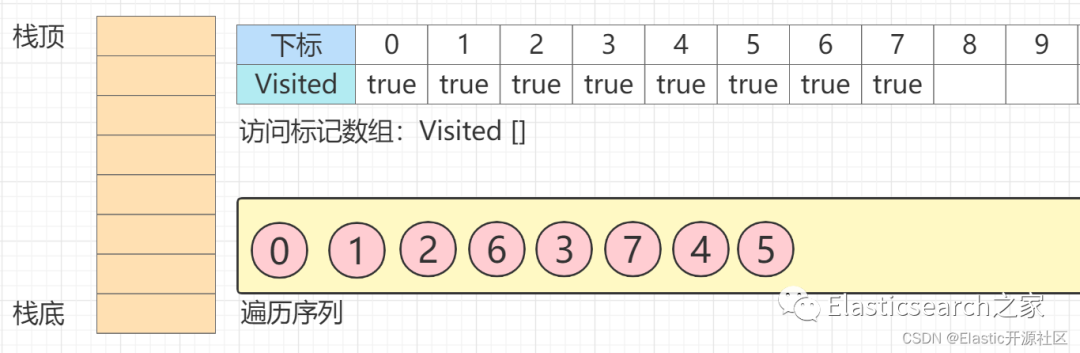
第14步 此时,节点8
入栈,节点8
所有邻接点均已访问,节点8
出栈,而后,节点9
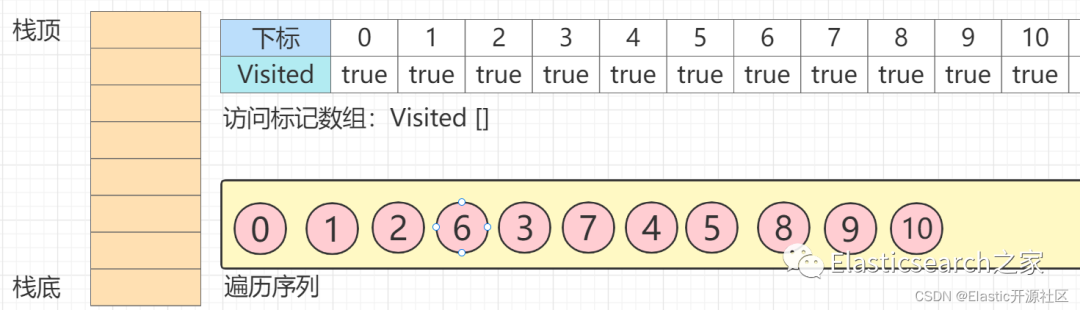
入栈,而后马上出栈。以此类推,最后,节点10
入栈,而后而后马上出栈,生成最终序列,如下图所示
4.6 树的深度优先搜索
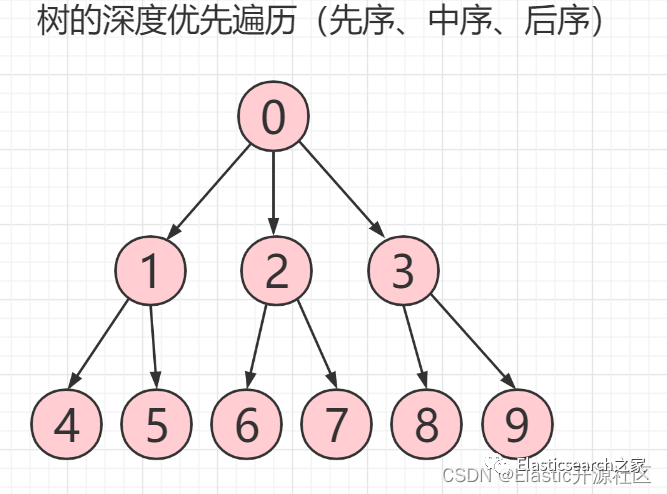
由上所述遍历过程,树的深度优先遍历序列如下图所示

4.7 动画演示深度优先搜索
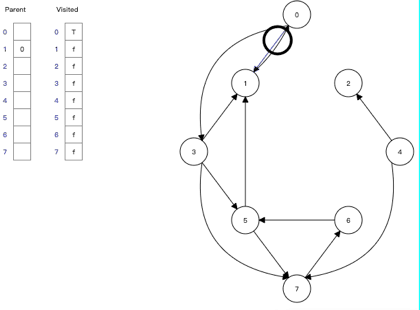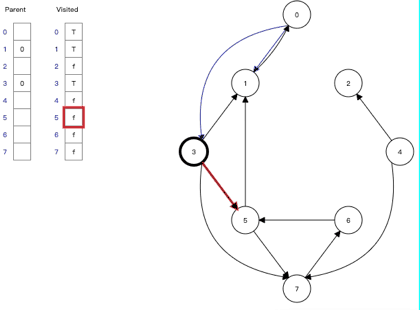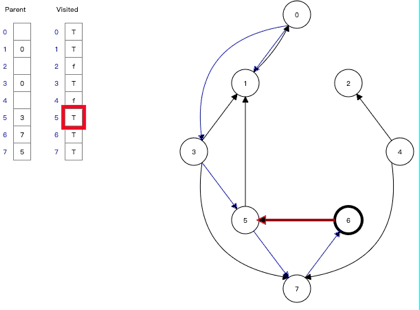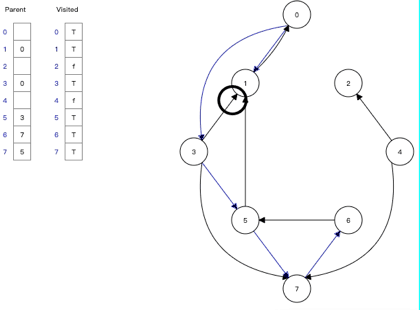
5、广度优先搜索(Depth-First Search)
5.1 图的广度优先搜索
和树
不同,图没有根节点,并且是可以回溯的,比如下图所示,为一个 8 节点的图搜索表示
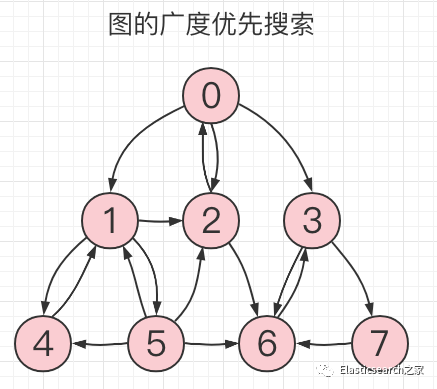
其中:
•节点0 :包含三个出度,分别指向其三个邻接点,分别为节点1、节点2、节点3
,同时节点0
也是节点2
的邻接点。•节点1:包含三个邻接点,分别为节点2、节点4、节点5
•节点2:邻接点为节点0、节点1、节点6
。•节点3:邻接点为节点6、节点7
。•节点4:邻接点为节点1
。•节点5:邻接点为节点1、节点2、节点4、节点6
。•节点6:邻接点为节点3
。•节点7:邻接点为节点6
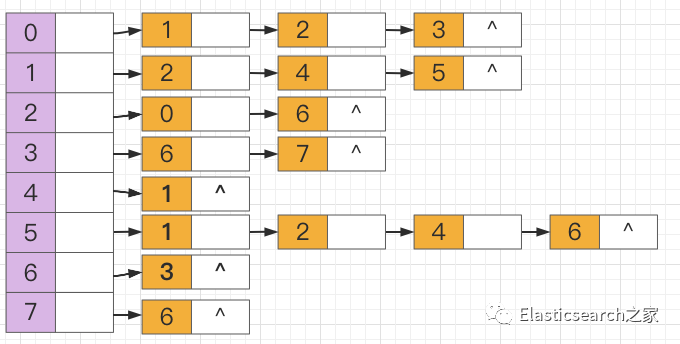
5.2 邻接表
下图为 2.1 中图搜索所示图
的邻接表形式。可以看到,节点7、节点8、节点10
是没有任何出度和邻接点的。
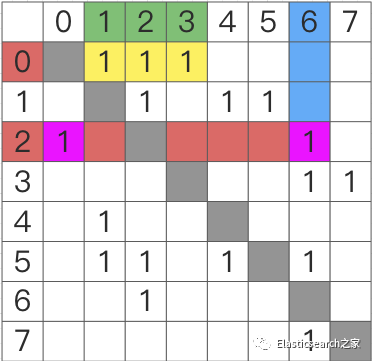
5.3 邻接矩阵
下图为 2.1 中图搜索所示图
的邻接矩阵
表示
其中,纵坐标表示 出度节点,横坐标表示 邻接点
比如,下图中:
•节点0:邻接点为节点1、节点2、节点3
•节点3:邻接点为节点0、节点6
5.4 图的广度优先搜索遍历过程
5.4.1 队列
图的广度优先遍历是靠队列
来完成的,我们首先创建一个空队列

5.4.2 Visited数组

我们借助 Visited数组,来标识当前节点 n 是否被访问过,空值代表 false.
5.4.3 遍历序列
准备一个空的遍历序列,用来存放最终生成的访问元素。

5.4.4 遍历过程
首先,图是没有根节点的,我们可以以任何节点作为其起始节点,下面我就以节点0
为起始节点为例,演示一下图的广度优先搜索过程。
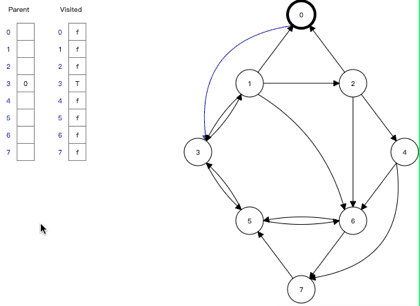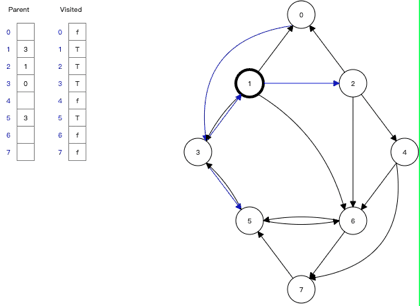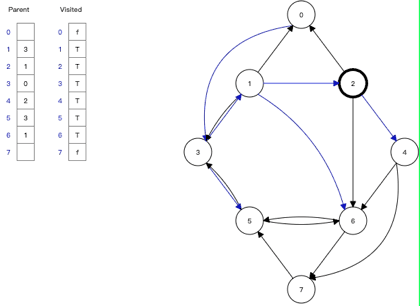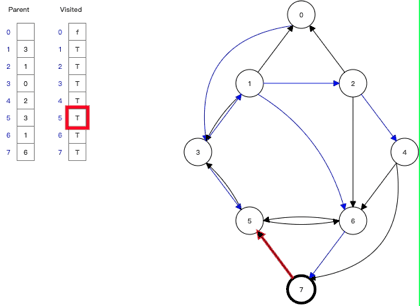
第1步 节点0
入队列

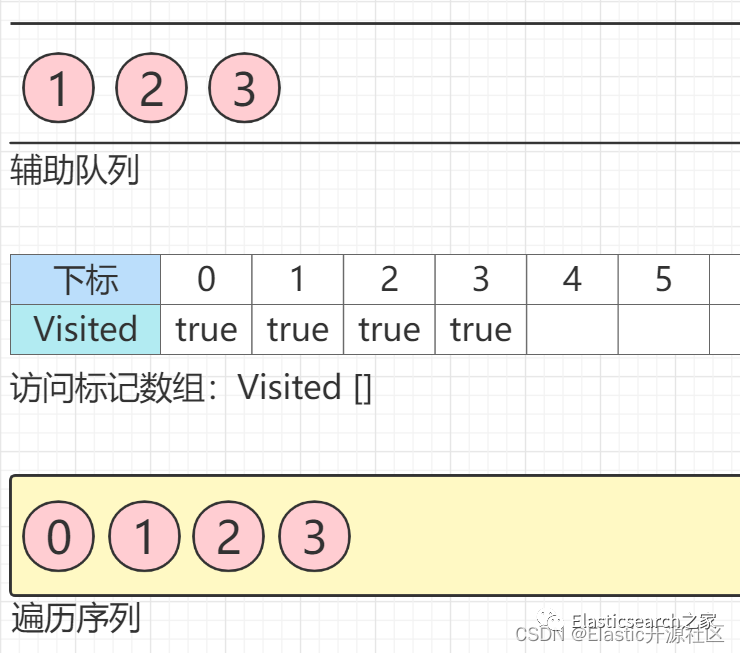
第2步 节点0
出队列,并且节点0
的所有邻接点入队列
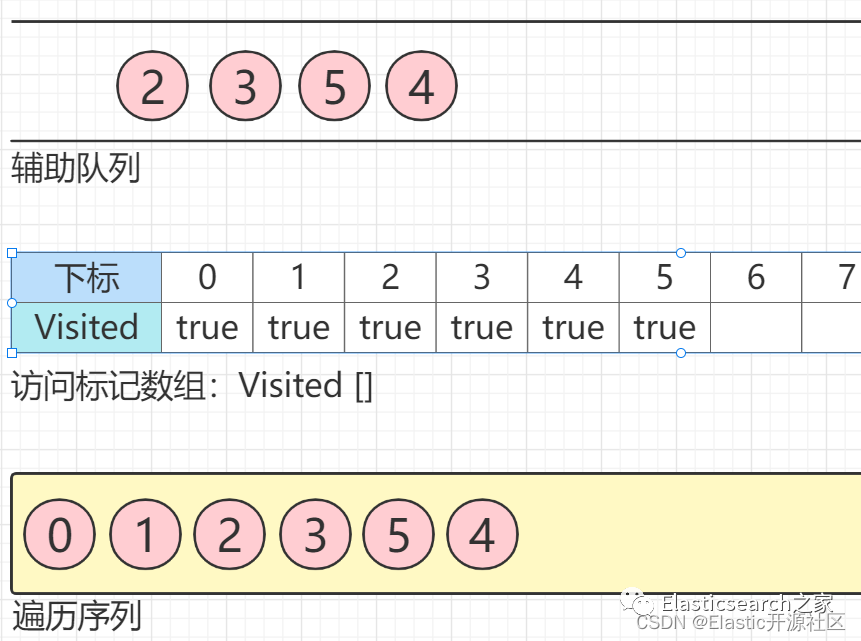
第3步 节点1
出队列,节点1
的邻接点入队列,但是此时,节点1
的邻接节点节点2
已经被访问过了,因此节点5、节点4
进队列
第4步
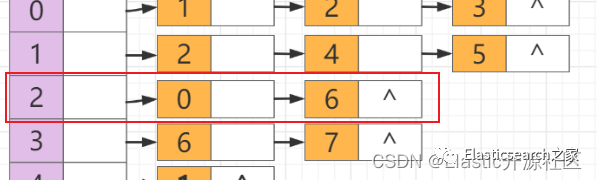
节点2
出队列,节点2
有两个邻接节点,其中节点0
已经被访问,因此,节点6
如队列
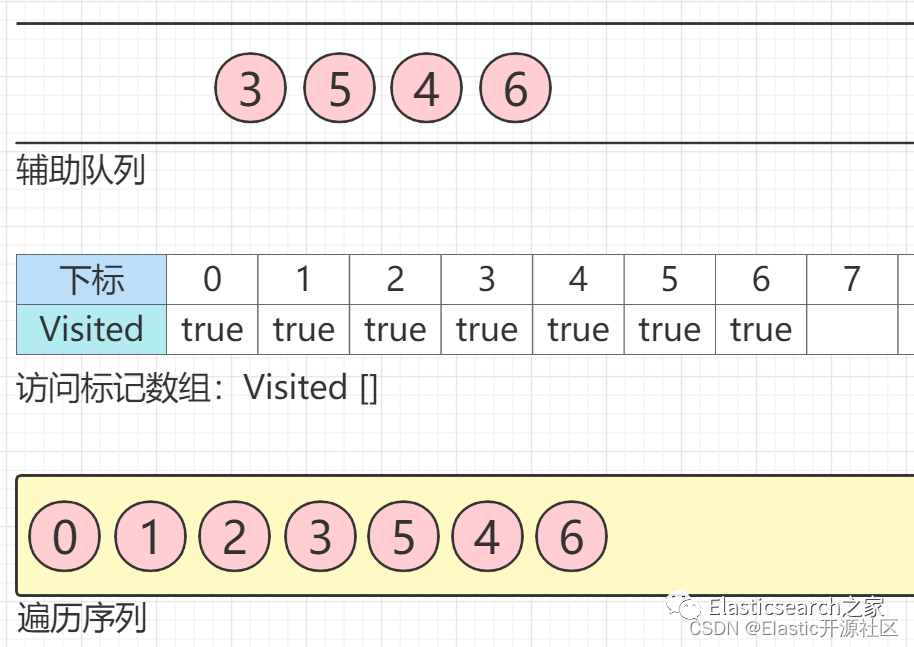
第5步 节点3
出队列,节点3
有两个邻接节点,其中节点6
已经被访问,因此,节点7入
队列
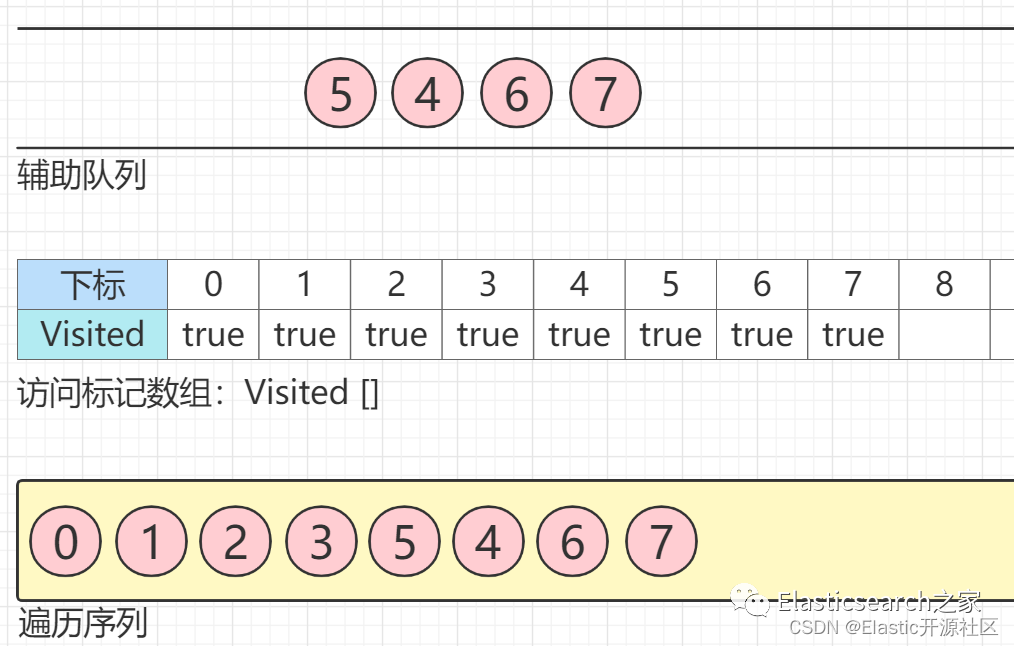
第6步
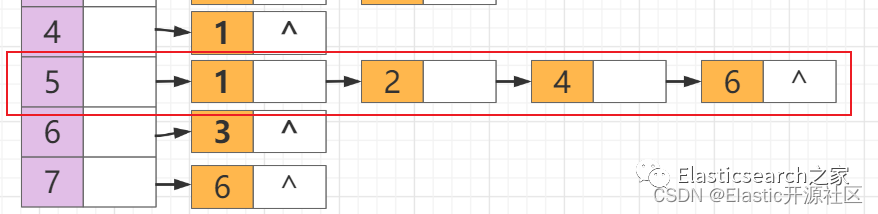
节点5
出队列,节点5
有四个邻接节点均已被访问,此时无节点入队列。同理,节点6、节点7
出队列,最终生成的遍历序列如下图所示
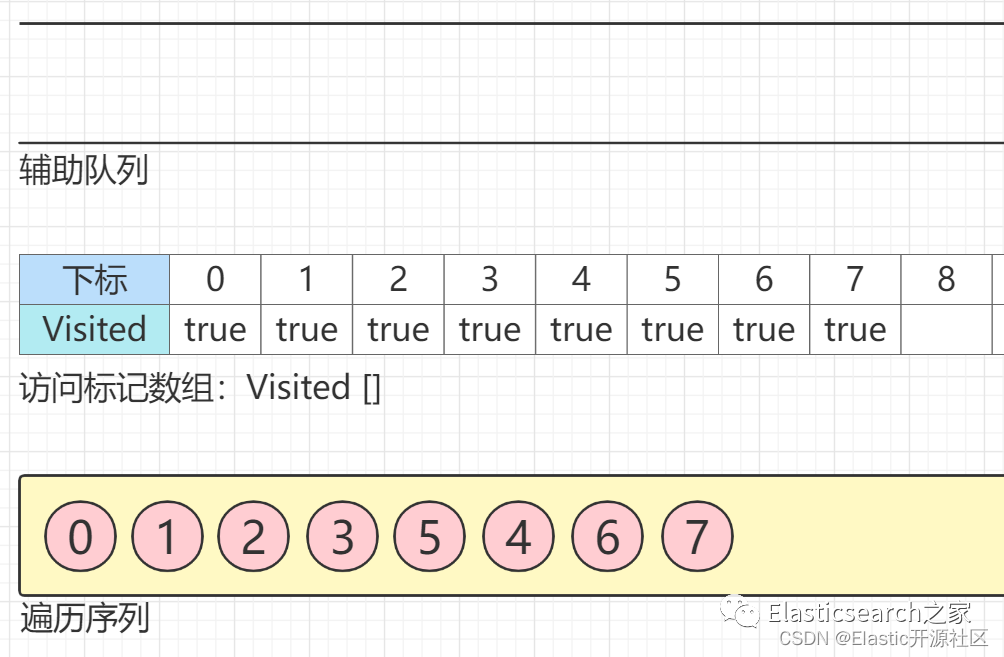
5.5 动画演示
扫码免费领取 ES 8.x 学习资料

Elastic开源社区
点赞分享加关注
学习唠嗑两不误

你们点点“分享”,给我充点儿电吧~






