「题目」：COLD BREW: DISTILLING GRAPH NODE REPRESENTATIONS WITH INCOMPLETE OR MISSING NEIGHBORHOODS
「作者」：Wenqing Zheng, Edward W Huang, Nikhil Rao, Sumeet Katariya, Zhangyang Wang, Karthik Subbian
「论文链接」：https://openreview.net/forum?id=1ugNpm7W6E
「代码」：https://github.com/amazon-research/gnn-tail-generalization
Introduction
图神经网络 (GNN) 在图分类、节点分类、链接预测和推荐等广泛的任务中实现了最先进的结果。大多数 GNN 依赖于消息传递的原理，从其（多跳）邻域聚合每个节点的特征。GNN 的成功依赖于「密集和高质量连接的存在」。
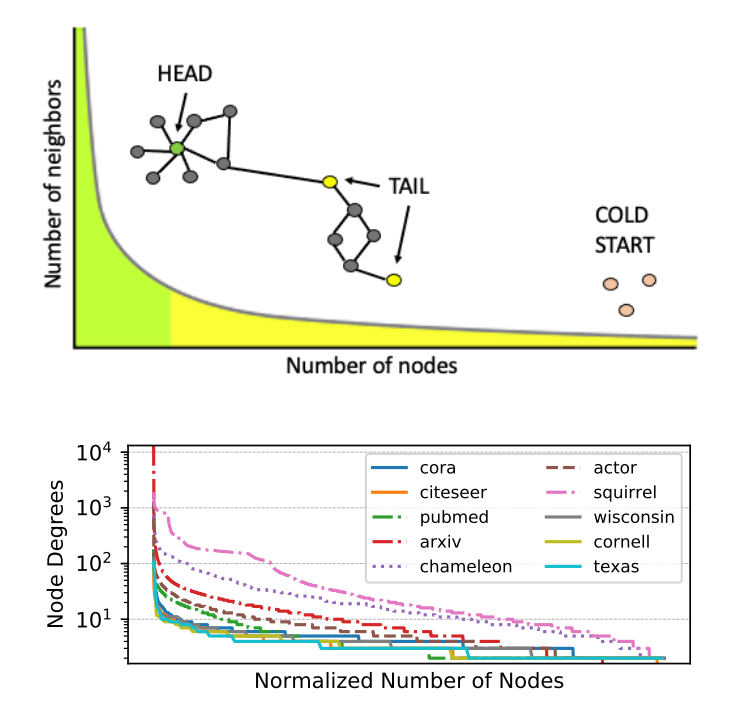
但是，许多现实世界图中存在的长尾节点度分布。具体来说，节点度分布本质上是幂律分布，大多数节点的连接很少。许多信息检索和推荐应用都面临严格冷启动（Strict Cold Start， SCS）的场景， 其中一些节点没有连接的边。诚然，预测这些节点比图中的尾节点更具挑战性。「在这些情况下，由于邻域的稀疏性或缺失，现有的 GNN 表现不佳。」
在本文中，作者提出了具有真正归纳能力的 GNN 模型：可以为图中的“孤立”节点学习有效的节点嵌入。这种能力对于充分发挥大规模 GNN 模型在具有「长尾和许多孤立节点」的现代工业规模数据集上的潜力非常重要。
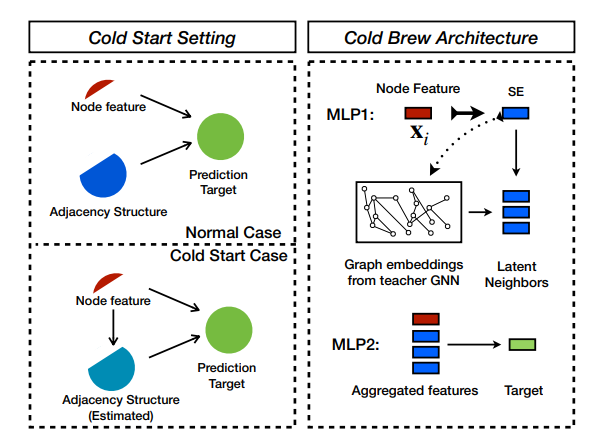
Cold Brew 框架解决了两个关键问题：-（1）如何有效地提炼教师的知识以进行尾部和冷启动，以及（2）学生如何利用这些知识。作者通过使用知识蒸馏学习潜在的节点嵌入来回答这两个问题，这既避免了“过度平滑”，又发现了潜在的邻域， SCS 节点缺少这些。与传统的知识蒸馏（Hinton et al., 2015）相比，本文的目标不是训练一个更简单的学生模型来像更复杂的教师一样执行。相反，是训练一个在泛化到尾部或 SCS 样本方面优于教师的学生模型。
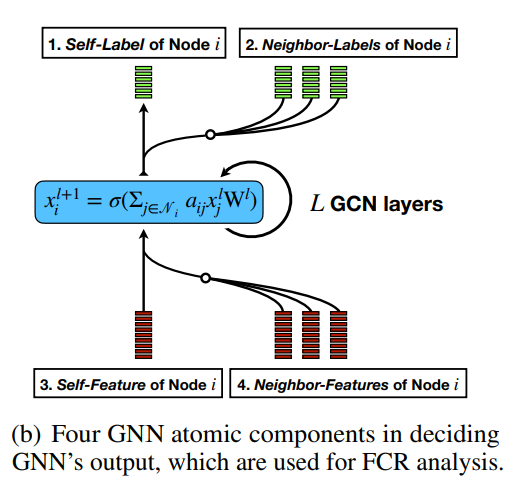
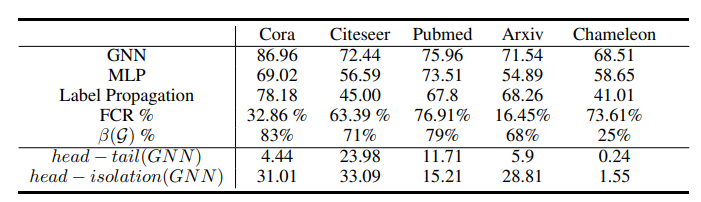
此外，为了帮助选择冷启动友好模型架构，作者提出了一个称为特征贡献率 (FCR) 的指标，用于量化节点特征对特定下游任务数据集中邻接结构的贡献。FCR 指示了推广到尾节点和冷启动节点的难度级别，并指导在 Cold Brew 中对教师和学生模型架构的原则选择。
本文主要的方法
本文的关键思想如下：GNN 将节点特征映射到 d 维嵌入空间，由于节点的数量 N 通常远大于嵌入维数 d，因此最终会得到该空间的过完备集使用嵌入作为基础。这意味着任何节点表示都可以转换为 K<<N 个现有节点表示的线性组合的可能性。本文目标是训练一个学生模型，该模型可以准确地发现目标孤立节点的最佳 K 个现有节点嵌入的组合。将此过程称为潜在/虚拟邻域发现，这相当于使用 MLP 来“模仿”教师 GNN 学习的节点表示。
作者采用知识蒸馏程序来提高尾部和冷启动节点的学习嵌入质量。使用教师 GNN 模型通过利用图结构将节点嵌入到低维流形上。然后，学生的目标是学习从节点特征到该流形的映射，而无需了解教师所拥有的图。进一步的目标是让学生模型推广到教师模型失败的 SCS 案例，而不仅仅是像标准知识蒸馏那样模仿教师。
TEACHER MODEL
考虑一个图 。对于具有 层的图卷积网络，第 层变换可以写为 ，其中 是标准化邻接矩阵， 是对角线度数矩阵， 是邻接矩阵。 是第 层的节点表示， 是特征变换矩阵，其中 的值取决于层 for , (d hidden, for , and 为 是应用于每一层的非线性函数，（例如，ReLU）。规范 指的是可选的批处理或层规范化。
GNN 通常会出现过度平滑，即节点表示变得彼此过于相似。受 Transformers (Vaswani et al., 2017) 中位置编码的启发，本文训练教师 GNN 学习一组可以附加的额外节点嵌入，称之为结构嵌入 (SE)。SE通过梯度反向传播学习除了原始节点特征（例如半监督学习中的节点标签）之外的额外信息。SE 的存在避免了 GNN 中的过度平滑问题：应用于不同节点的变换对于每个节点不再相同，因为每个节点的 SE 不同并参与特征变换。
具体来说，对于每一层 ，结构嵌入采用可学习矩阵 的形式，SE-GNN 层向前通行证可以写成：
「Remark 1」：注意SE与传统特征变换中的偏置项;在偏置 中，行在所有节点之间复制/共享。相反，作者对每个节点都有不同的结构嵌入。
「Remark 2」：SE 也不同于传统的标签传播 (LP) 。LP 通过迭代 ，其中 是用于训练节点类和零用于测试节点的 ground truth 的 one-hot 编码， 是混合的部分每次迭代。
SE-GNN 使节点 能够学习通过 将自身和邻居的标签信息编码到自己的节点嵌入中。本文使用 Graph Convolutional Networks (Kipf & Welling, 2016)，结合最近文献中提出的其他构建块，包括：(1) 初始/密集/跳跃连接，和 (2) 批处理/对/节点/组归一化作为Cold Brew 的老师 GNN 的骨干。作者还将正则化项应用于损失函数，产生以下损失函数：
其中 是模型在第 层的嵌入， 是模型输出 和训练集上的ground truth ， 是正则化系数（在实践中对不同数据集进行网格搜索）。根据任务，交叉熵损失可以用任何其他适当的损失代替。
STUDENT MLP MODEL
本文将学生设计为由两个 MLP 模块组成。给定一个目标节点，第一个 MLP 模块模仿 GNN 教师生成的节点嵌入。接下来，给定任何节点，从图中找到该节点的一组虚拟邻居。最后，第二个 MLP 同时关注目标节点和虚拟邻域，并将它们转换为感兴趣的嵌入。
从标签平滑的角度解释模型
(Wang & Leskovec, 2020)定理1表明标签预测的误差是由邻域聚合后特征的差异决定的：如果差异很大，那么标签预测的误差也很大，反之亦然 具体定理如下：
(Wang & Leskovec, 2020) 定理 1：假设从节点特征到节点标签的潜在 ground-truth 映射是可微的和 L-Lipschitz。如果边权重 在其直接邻居上近似平滑 ，误差 ，即 ，然后是 也近似平滑 到误差 )，其中 o 表示高阶无穷小。
该定理表明标签预测的误差是由邻域聚合后的特征差异决定的：如果很大，那么标签预测的误差也很大，反之亦然。然而，通过结构嵌入，每个节点 在聚合过程中也会学习一个独立的嵌入 ，这会改变 转化为 。从这个定理推导出来，结构嵌入 对于教师模型很重要：它在学习节点之间的残差差异时具有更高的灵活性和表现力，因此误差 \overline{\mathbf{E}} 可以降低。
从这个定理中，我们也可以看到引入像 Cold Brew 学生模型那样的邻域聚合的必要性。如果在没有邻域聚合的情况下直接应用 MLP 模型，则 i 是不可忽略的，导致标签预测的损失更大。但是，Cold Brew 引入了邻域聚合机制，以便学生 MLP 的第二部分接管第一个 MLP 生成的邻域聚合。因此，即使在没有实际邻域的情况下，Cold Brew 也能消除上述残差
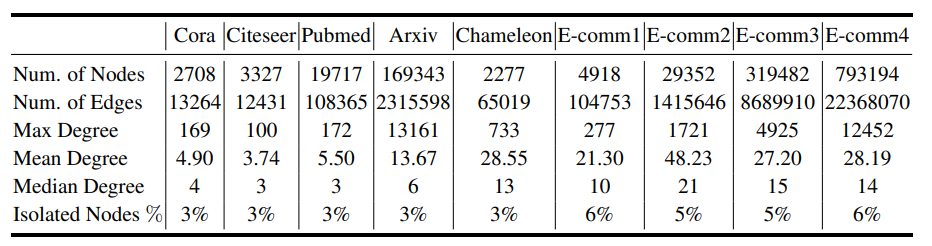
实验
结论
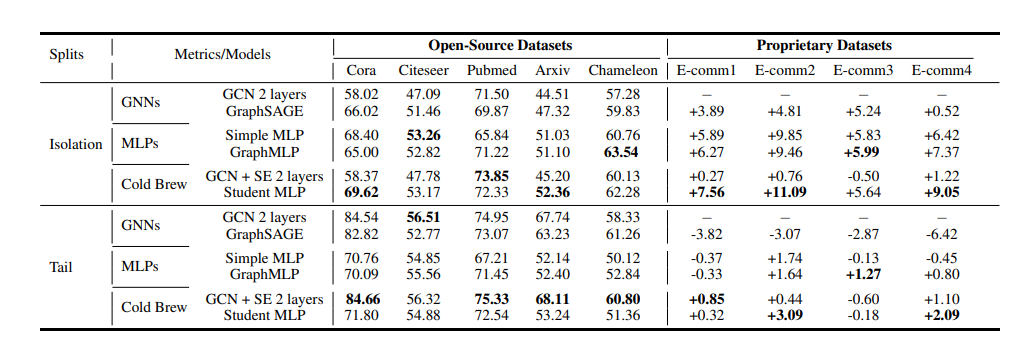
本文研究了将 GNN 推广到尾部和严格冷启动节点的问题，这些节点的邻域信息要么稀疏/嘈杂，要么完全缺失。作者提出了一种师生知识蒸馏程序，以更好地推广到孤立节点。本文在 GNN 层中添加了一组独立的结构嵌入以缓解节点过度平滑，并为学生模型提出了一个虚拟邻居发现步骤以关注潜在邻域。还提出了 FCR 指标来量化真正归纳表示学习的难度并优化我们的模型架构设计。实验证明了提出的框架在公共基准和专有数据集上的一贯优越性能。
