前沿
已经有一年没有深入研究算法模型了，不过这段时间做的工程工作也很有意思。想着老大哥说不做总结的知识很快就会忘记，所以想在还没有完全忘光之前，把这些记忆的碎片留存下来。同时最近看了比较多的训练框架论文，也想结合模型侧和工程侧的训练来谈谈目前对这个领域的理解。
这篇文章想先讲讲对推荐精排模型的理解。下一篇讲训练引擎，比如大规模的分布式训练，KV Embedding，IO样本流这些，这些也都是各大厂搜广推训练优化的核心。在线serving的链路做的不多，希望以后有机会也能写写。
Overview
这次我们主要讲讲搜广推中的推荐模型（搜索，广告和推荐是互联网的三大核心应用），其实搜广推三个方向上的技术栈都大差不差。一个推荐系统大致由召回和排序两个阶段组成，其中召回主要用于召回需要推荐的item（主要根据不同的策略进行多路召回，比如用户标签，或者简单的模型，比如CF，召回候选的item集给后续排序模型使用）；排序阶段主要使用复杂的模型，而根据其业务，数据量级，算力和技术的不同，排序阶段还会分出粗排，精排和重排这些细粒度的阶段，但本质都是尽量在最后使用复杂的模型对少量的item进行精准的排序，最后排序结果会结合业务逻辑进行千人千面的展示。这其实也是淘宝上推荐商品，抖音和Youtube推荐视频的大致过程。其实支付上的业务风控也是一样，支付风控上会主要分为可信和非可信两个阶段，其认为大部分交易都是值得信任的，然而计算资源是有限的，我们需要尽量使用有限的计算资源对那部分高风险非可信的交易使用复杂模型和业务逻辑进行精准的识别，而可信的交易只使用简单的策略或者模型进行防控。
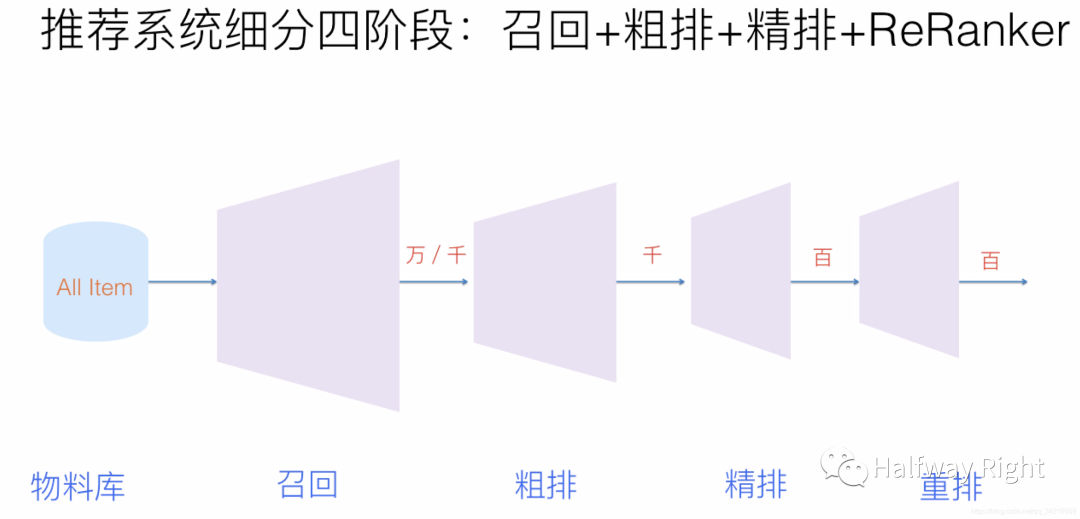
这四个阶段中，精排阶段是推荐系统产生效果的重点，也是深度学习应用最广泛的场景，目前精排阶段的模型论文主要集中在：
自动提取高阶特征，如DeepFM, xDeepFM
序列推荐，如Autoint，DIN，DIEN
CTR和CVR的联合建模进行多目标学习，如ESMM，MMoE
其他还有多模态，基于graph或者强化学习的推荐方向，其实推荐领域主要是把各个机器学习子领域有效的方法应用到推荐系统当中。
这篇文章我们主要介绍最为经典的Factorized Machine(因子分解机，FM)，这在数据不是太丰富的业务场景仍然是主要模型。Factorized Machine是在推荐模型中应用最为广泛的模型结构，其衍生出了DeepFM，NFM，AFM和xDeepFM等一系列FM类的论文。个人理解，FM一直这么火热的原因在于 1. 自动进行特征的交叉组合 2. 工程实现简单和计算量低。3. 泛化性能好。
为什么需要FM模型？
逻辑回归
在讲FM之前我们先讲讲逻辑回归Logistic Regression是如何引入交叉特征的，这比较好解释FM模型的贡献。假设一个简单的逻辑回归模型，其本身由一个线性模型
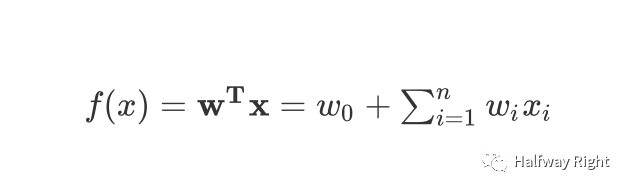
和 一个 response function组成 (从y服从Bionomial Distribution可以推导出逻辑回归的response function是logistic function)，则逻辑回归可建模为
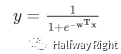
但是显然可以发现其中的线性模型部分只是特征的线性组合，无法捕获到非线性特征，所以逻辑回归本身需要通过增加人工的特征组合的方式引入非线性特征。
加入特征交叉的逻辑回归
我们可以通过人工添加x_i 和x_j的交叉项来增加模型的非线性，那么这个模型的线性部分就会变成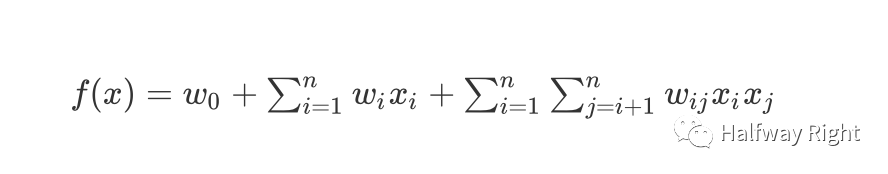
上述模型也可以视为使用多项式核函数的支持向量机。从统计学习的角度，新增的这一项我们也叫做interaction，虽然Linear Fixed Model的理论更多是为了通过该项表现不同explantory variable对response variable的共同作用。举个例子，假如我们对一个用户是否会购买冲浪板进行二分类建模，会发现城市类型和年龄阶段两个explantory variable的组合是对用户是否会购买冲浪板的判断是的一个有效特征组合，因为在靠海边城市的青少年人更倾向于去买冲浪板，所以城市类型和年龄阶段是一个有效的组合特征，而通过其权重大小可以解释该项的重要性。
虽然通过增加人工特征组合的方式，逻辑回归模型可以捕获二阶特征，但有以下缺点：
搜广推场景主要是大规模稀疏数据。这使得w_ij难以预估，可以想象上述模型只有当x_i和x_j同时出现的时候，参数w_ij才可以更新，这造成了interaction项的预测效果差和泛化能力弱。（虽然例子里的城市类型和年龄阶段很好采集到，但是大部分特征无法采集或者特征数量级大造成的高维稀疏性）
参数量显著增大。w_ij的参数量级是O(n^2)。而先前一版的模型参数只有O(n)。这样给存储和计算都带来巨大压力。
人工组合特征成本高。
其实，各大公司仍然有专门的C++ library在训练前的预处理阶段用于特征的非线性组合（特征工程），比如凤巢的FeatureExtract和阿里妈妈的FG，来保证在离线的预处理一致性。
Factorized Machine
FM模型
那FM是如何解决上面的问题的？我们用v_i和v_j的点积代替上述的interaction项，w_ij x_i x_j，其中v_i和v_j分别是特征i和j的隐向量，那么线性部分变为
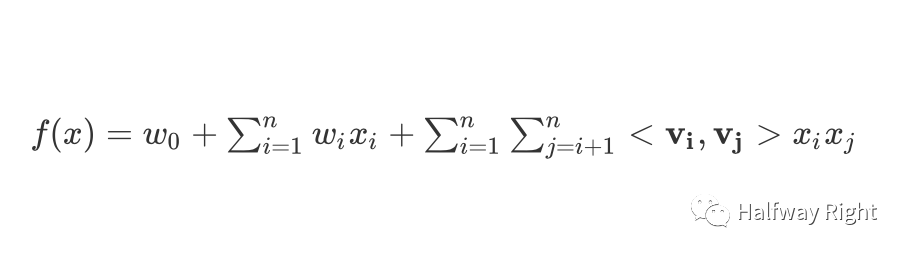
对于隐向量，当前都是使用ID化+Embedding Lookuptable的方式查出其Embedding Vector作为隐向量(对于multivalent特征通过embedding_lookup_sparse做combine；Old-fashioned的方式也可以使用Onehot的输入和W去做矩阵乘法)。Embedding Lookuptable最早来自于NLP模型，从Microsoft的DSSM开始，Embedding Lookuptable的技术已经成为搜广推中表征categorical feature语义的基操。假设v_i是城市类型，有两个枚举值“北京”和“海口"，我们分别用两个dense vector来表达北京和海口在embedding space中的语义。假设v_j是年龄阶段，也有两个枚举值 "青少年"和"中老年"。那么相比于原来一条样本里需要城市类型和年龄阶段两个特征同时出现或者都有值，上面的逻辑回归才能估计w_ij，FM可以利用城市类型或者年龄阶段出现时候的数据来估计v_i和v_j（比如估计城市类型这个特征列的隐向量参数时，只要一条样本里城市类型该特征列有值即可，而不一定需要年龄阶段这个特征列有值），这样不仅解决了数据稀疏场景下对x_i和x_j交叉项的参数估计，也增加该交叉项的泛化性。
FM上的空间和计算优化
关于空间复杂度，我们可以计算下FM的参数量，v_i一般使用k维向量进行表征（其中k是embedding_size，一般是8， 16等常数级），那么易得整个interaction部分的参数量级是O(kn)
，其中k是一个常数项。而在加入了特征交叉项的逻辑回归中的interaction项的参数量是O(n^2)。使用FM以后，整个交叉项的参数量级从平方级降低到线性级。
关于时间复杂度，如果我们直接用上面的公式去计算FM，我们的时间复杂度也是O(n^2)，因为我们需要两个for循环来计算v_i v_j。那么通过下面的公式推导(Rendle, 2020)，易得最后这个熟悉的sum_square - square_sum的计算公式，这样我们只需要一个for循环就可以完成FM的计算(k是隐向量维度)，整个计算复杂度也降低为O(kn)。
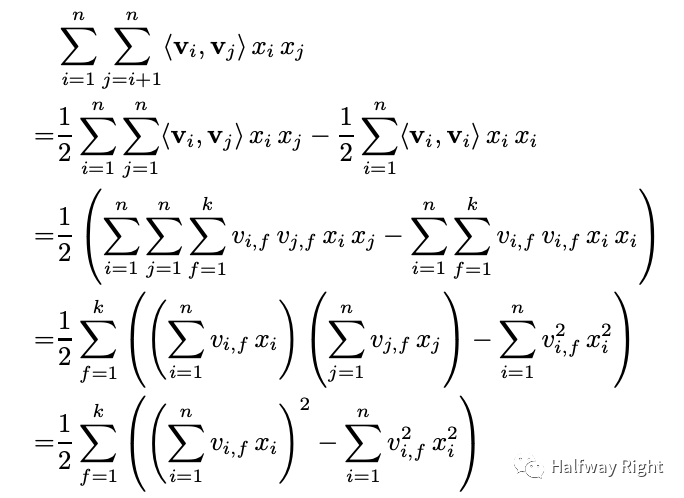
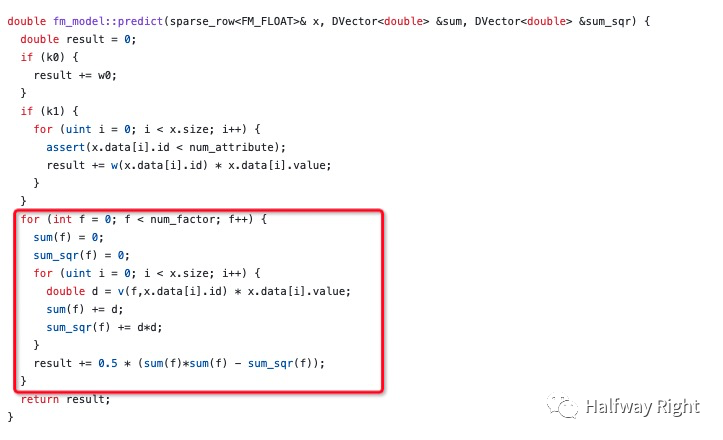
libFM C++版本实现 (Onehot输入版本)
DeepCTR中FM Tensorflow版本实现(Embedding Lookup版本)
相关论文
自从Rendle在2010年提出用FM以后，衍生出一系列FM相关论文，大致总结了下这些论文的思路及工程上的空间复杂度和时间复杂度（其中n代表特征数，K代表embedding vector的维度）。
FFM: FFM模型相比于FM引入了域(Field)的概念，认为同域的特征之间存在共性，而异域的特征之间存在差异性。相比于FM中，特征x_i与其他特征x_j进行交叉的时候仅使用一个隐向量v_i，FFM为每个特征x_i定义了F-1个隐向量，作为和不同域的特征交叉的隐向量（这里的域其实就是特征列，因为在one hot encoding中无法区分不同的特征枚举值，如两个特征的性别（枚举值为男，女）和操作系统类型（枚举值为mac, windows）经过onehot后就抹去了特征field的概念，假如一条样本“男，mac”，则onehot encoding为 [1, 0, 1, 0]，其实这个vector index 0和1的位置都是代表性别，为同域特征）。假如每个特征都各自有个特征域，即每个特征就有n-1个隐向量来表达和其他特征域下特征的交叉，容易推导出FFM的空间复杂度相比于FM多了一个F-1因子，而时间复杂度同优化前的FM一样，都是O(k n^2)，但无法像FM展开到线性级的复杂度。
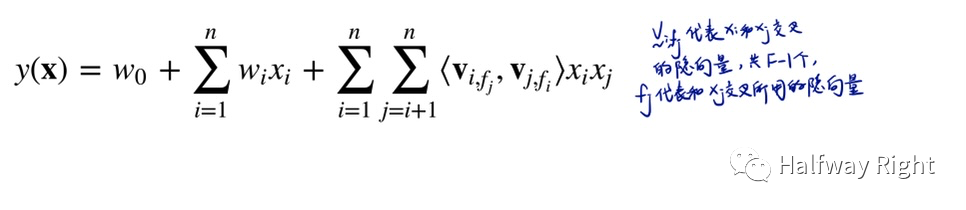
FNN: 相比于FM只能捕获到二阶交叉特征，FNN在FM后接入MLP用于捕获更高阶交叉特征。其采用两阶段而非端到端的方式进行训练，首先通过FM对高维稀疏数据进行预训练得到初始化的Embedding Vector参数，然后接入MLP进行finetuning。个人感觉这篇在2016发表的论文，其采用FM对高维稀疏数据进行预训练得到embedding vector，再进行finetuning的思想在今天也并不过时。
NFM： 相比于FM两个embedding vector做dot product，NFM提出的FM(Bi-Interaction Layer)是用的element-wise product（实现上其实相比于FM少了个sum pooling，其输出是K维的，而标准FM的输出是scalar），而后接入MLP用于捕获更高阶交叉特征。
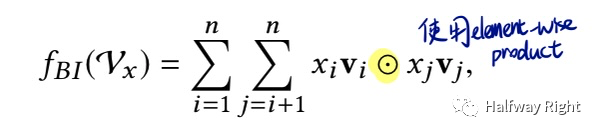
DeepFM: 相比于NFM，DeepFM把FM作为了Wide层（看代码实现也是比标准FM少个sum pooling），Deep层仍然采用MLP，避免wide层进行人工特征组合。从代码实现上，NFM和DeepFM一个是串行FM without sum pooling + MLP，一个是并行。
AFM：AFM通过Attention为不同的二阶特征组合显式地提供了重要性的权重（非QKV，而是用MLP估计二阶交叉的权重），但其计算复杂度和空间复杂度都是平方级，由于显式为交叉项赋attention权重，无法像FM一样展开到线性级的复杂度。
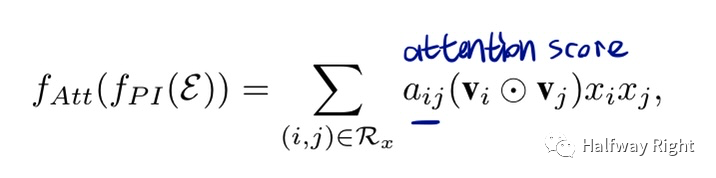Deep & Cross Network: Deep & Cross将Cross Network作为wide层，通过MLP的中间结果和输入做外积自动构建高阶交叉特征（其通过网络的深度来控制交叉的阶数），不过其学习的目标是残差。因为Deep & Cross只有MLP的weights，其空间复杂度和时间复杂度，和中间层神经元个数恒等于输入维度的MLP相同。
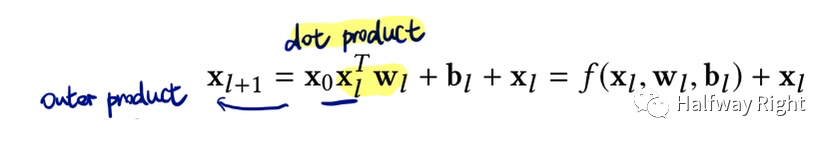
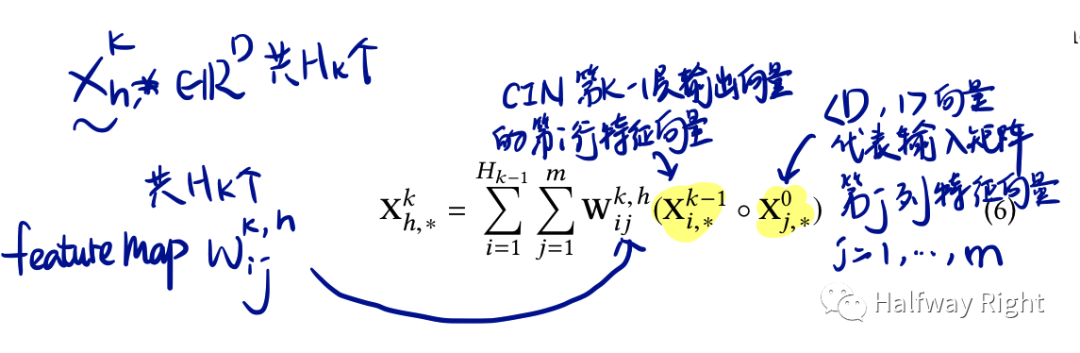
xDeepFM：虽然xDeepFM名字和DeepFM很像，但其主要对比的是Deep & Cross bit-wise fashion的特征交叉方式（个人理解MLP和Deep&Cross都是bit-wise的interaction，因为都需要把n个特征的embedding vector flatten到一个维度喂入神经网络，抹去了特征的概念），而xDeepFM强调采用vector-wise fahsion显式地进行高阶的特征交叉，其实是把输入embedding vector和中间层输出的embedding vector做外积，然后通过一维卷积去进行压缩编码，最后sum pooling以后concat进行输出。（其通过显式的外积保证了embedding vector的元素或者bit之间不会相互交叉，比如X_0的embedding vector为[D, 1]的第一个元素[1,1]不会和[2,1]个元素进行交叉，其只能和中间层各特征embedding vector的第一个元素交叉）。
关于空间复杂度和时间复杂度，L代表CIN层数，H_k代表每层CIN的Feature map数，其中H_0为n，假设于H_i * H_j 约等于H^2。那么可以推导出xDeepFM空间复杂度为L层CIN Layer中卷积核的参数量级，即O(nLH^2)，而其时间复杂度高达O(nkLH^2)。
总结
综上所述，FM在大规模稀疏数据场景可以有效地学习到泛化性更好的二阶交叉特征，并在计算上有着优秀的时间复杂度和空间复杂度，使得其仍然是很多公司线上精排模型的首选。下一篇文章会主要讲讲业界在搜广推场景大规模训练中碰到的问题和主流解决方案。其实早期看到的很多推荐论文比较偏学术性，无法在工业级的大数据量级下进行训练和低延迟的在线推理，不过这块其实涉及了整个架构的设计（包括特征工程，这两天也在思考稀疏特征的存储和解析这些算法和工程Co-Design的问题），希望能有一天梳理出来。
Reference
各论文，源码，DeepCTR，深度学习推荐系统和技术博客。
封面图片：Atey Ghailan
