R语言中使用RCPP并行计算指数加权波动率

原文链接：http://tecdat.cn/?p=17829

指数加权波动率是一种波动率的度量，它使最近的观察结果有更高权重。我们将使用以下公式计算指数加权波动率：

S [t] ^ 2 = SUM（1-a） a ^ i （r [t-1-i]-rhat [t]）^ 2，i = 0…inf

其中rhat [t]是对应的指数加权平均值

rhat [t] = SUM（1-a） a ^ i r [t-1-i]，i = 0…inf

上面的公式取决于每个时间点的完整价格历史记录，并花了一些时间进行计算。因此，我想分享Rcpp和RcppParallel如何帮助我们减少计算时间。

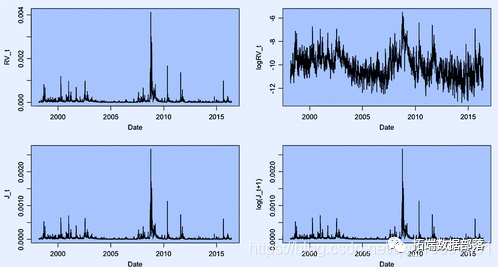
我将使用汇率的历史数据集  作为测试数据。

首先，我们计算平均滚动波动率

#*****************************************************************
# 计算对数收益率
#*****************************************************************
ret = diff(log(data$prices))
 
tic(5)
hist.vol = sqrt(252) * bt.apply.matrix(ret, runSD, n = 200)
toc(5)

经过时间为0.17秒

接下来，让我们编写指数加权代码逻辑

# 建立 RCPP 函数计算指数加权波动率  
load.packages('Rcpp')
sourceCpp(code='
#include <Rcpp.h>
using namespace Rcpp;
using namespace std;
 
// \[\[Rcpp::plugins(cpp11)\]\]
 
//ema\[1\] = 0
//ema\[t\] = (1-a)\*r\[t-1\] + (1-a)\*a*ema\[t-1\]
// \[\[Rcpp::exp

 {
        if(!NumericVector::is_na(x\[t\])) break;
        res\[t\] = NA_REAL;
    }
    int start_t = t;
    
-a) * a^i * (r\[t-1-i\] - rhat\[t\])^2, i=0 ... inf
// \[\[Rcpp::export\]\]
NumericVector run\_esd\_cpp(NumericVector x, double ratio) {
    auto sz = x.siz

    // find start index; first non NA item
    for(t = 0; t < sz; t++) {
        if(!Num
0;    
    for(t = start_t + 1; t < sz; t++) {
        ema = (1-ratio) * ( x\[t-1\] + ratio * ema);
        double sigma = 0;    
        for(int i = 0; i < (t - start_t); i++) {
            sigma += pow(ratio,i) * pow(x\[t-1-i\] - ema, 2);
        }
        res\[t\] = (1-ratio) * sigma;
    }    
, n, ratio = n/(n+1)) run\_ema\_cpp(x, ratio)
run.esd = funct

经过时间为106.16秒。

---

点击标题查阅往期内容

HAR-RV-J与递归神经网络（RNN）混合模型预测和交易大型股票指数的高频波动率

左右滑动查看更多

01

02

03

04

执行此代码花了一段时间。但是，代码可以并行运行。以下是RcppParallel版本。

# 建立 RCPP 并行函数计算指数加权波动率  
load.packages('RcppParallel')
sourceCpp(code='

using namespace Rcpp;
using namespace s
s(cpp11)\]\]
// \[\[Rcpp::depends(R
to read from
    const RMatrix<double> mat;
    // internal variables
    const double ratio
t;
    // initialize from Rcpp input and output matrixes
    run\_esd\_helper(const Nume
all operator that work for th

in, size_t end) {
        for (size_t c1 = begin; c1 < end; c1++) {        
            int t;
            // find start index; fir

经过时间为14.65秒

运行时间更短。接下来，让我们直观地了解使用指数加权波动率的影响

dates = '2007::2010'
layout(1:2)
e='h', col='black', plotX=F)
    plota.legend(paste('Dai
s,1\],type='l',col='black')

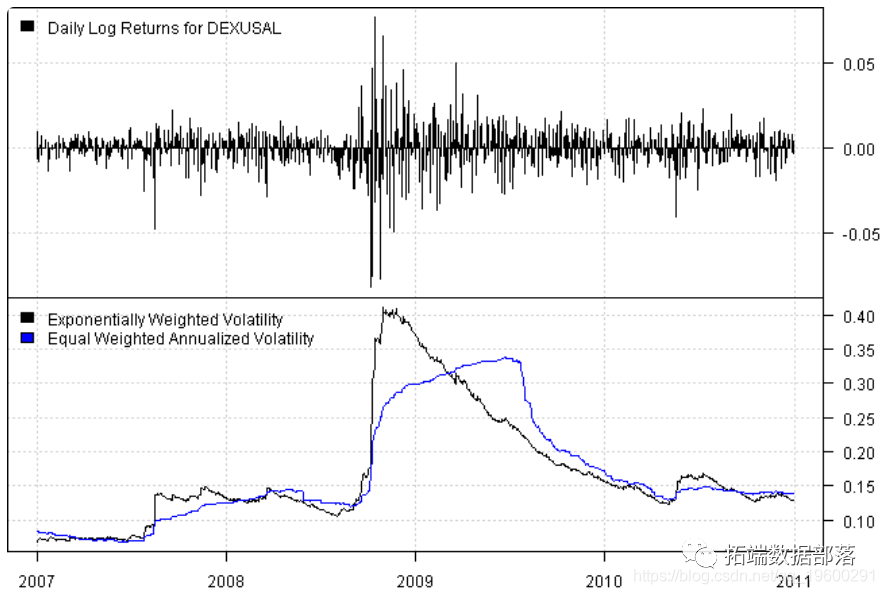
不出所料，指数加权波动率在最近的观察结果中占了更大的比重，是一种更具反应性的风险度量。

点击文末“阅读原文”

获取全文完整资料。