R语言数据分析|季节集中指数、地理集中指数与变异系数的计算

本文主要介绍如何利用R语言中的函数来计算论文中常见的季节集中指数、地理集中指数及变异系数。

1、季节集中指数

季节集中指数^[1]能够衡量地理要素在一年12个月内分布的集中程度。其计算公式如下，式中：R为季节集中指数，R值越大，表明地理要素在时间分布上越集中，Xi为地理要素在全年所占比重。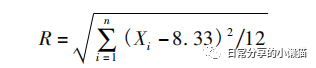

计算季节集中指数。以10个地区某项地理要素在一年内12月的分布数量为例，计算各地区该要素的季节集中指数。

setwd("C:\\Users\\Acer\\Desktop") #设置工作路径
seas <- read.csv("seas.csv") #读取数据
seas #查看数据
#   mon reg1 reg2 reg3 reg4 reg5 reg6 reg7 reg8 reg9 reg10
#1    1   33   23   23   44   38   33   45   22   31    33
#2    2   28   20   36   33   32   23   30   48   27    41
#3    3   38   35   24   32   49   27   18   30   34    26
#4    4   29   47   41   38   34   21   39   19   32    30
#5    5   37   31   42   36   33   38   46   16   47    37
#6    6   24   22   34   19   38   18   33   27   43    27
#7    7   23   24   44   36   36   35   15   48   19    36
#8    8   49   33   45   27   20   35   18   32   36    40
#9    9   25   24   34   47   30   28   31   36   33    38
#10  10   20   39   26   35   30   18   39   16   22    29
#11  11   37   33   28   47   16   46   30   43   19    46
#12  12   34   49   28   17   49   20   22   43   17    24
seas <- seas[,-1] #去除首列
apply(seas, 2, function(x) 
  sqrt(sum(((x/sum(x)*100) - 8.33)^2)/12)
  ) #计算季节集中指数
#季节集中指数结果
# reg1  reg2  reg3  reg4  reg5  reg6  reg7  reg8  reg9 reg10 
#2.081 2.434 1.878 2.254 2.301 2.508 2.763 3.018 2.546 1.606

2、地理集中指数

地理集中指数^[2]主要用来表征地理要素在空间分布上的集中程度，其取值范围在0~100之间，数值越大，表示地理要素的空间分布越趋于集中；反之，则越离散。地理集中指数计算公式如下，式中：Z为地理集中指数，Yi为第i个地区该地理要素的数量，T为地理要素总量，m为地区总数。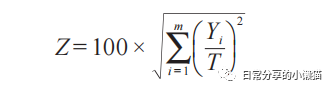

计算地理集中指数。以12个地区某项地理要素在2015-2020年内的分布数量为例，计算各年份该要素的地理集中指数。

geog <- read.csv("geog.csv")#读取数据
geog #查看数据
#     reg y2015 y2016 y2017 y2018 y2019 y2020
#1   reg1    27    42    46    33    37    42
#2   reg2    45    38    38    43    20    38
#3   reg3    31    15    27    20    30    48
#4   reg4    29    33    39    50    28    50
#5   reg5    26    24    42    31    17    26
#6   reg6    39    35    18    34    46    18
#7   reg7    41    44    34    47    25    25
#8   reg8    38    34    16    28    27    28
#9   reg9    22    46    24    18    44    22
#10 reg10    21    16    39    20    30    43
#11 reg11    19    21    41    30    42    22
#12 reg12    30    46    25    36    47    33
geog <- geog[,-1]#去除首列
apply(geog, 2, function(x)
  sqrt(sum((x/sum(x))^2)) * 100
  ) #地理集中指数
#地理集中指数结果
#y2015 y2016 y2017 y2018 y2019 y2020 
#29.85 30.40 30.10 30.20 30.13 30.30 

3、变异系数

变异系数^[3]能够消除量纲差异，在比较多组数据的离散程度时具有较好的适用性，其计算公式为原始数据的标准差与原始数据的平均值之比：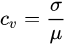

计算变异系数。以上文中计算地理集中指数的数据为例，计算各年份的变异系数。

apply(geog, 2, function(x) 
  sd(x)/mean(x)
  ) #计算变异系数
#变异系数结果
# y2015  y2016  y2017  y2018  y2019  y2020 
#0.2744 0.3445 0.3089 0.3204 0.3122 0.3334 

4、apply函数

本文主要使用apply函数进行公式计算，apply函数的基本形式为：

apply(X, MARGIN, FUN, ..., simplify = TRUE)

其中：x为数据对象，MARGIN=1表示对行进行操作，MARGIN=2表示对列进行操作，FUN是函数表达式，可以为基本的函数，如sum、mean、median、sd、var、range、min、max，也可以为任意指定的函数。本文即利用任意指定的函数来进行相关公式的计算。

5、其他

R语言能够将函数应用到向量、矩阵、数据框等一系列对象上，在数据的整理与在分析上具有快捷、高效的特点，同时在计算出数据后也能快速对数据进行可视化，完成数据的分析与绘图。后续也将继续推出利用R语言函数进行数据分析的其他方法。如需本文数据可在后台回复【20220107】获得。

如有帮助请多多点赞哦！

参考资料