R数据分析|数据的标准化、规范化与对数化

在进行回归分析或机器学习时，由于数据普遍存在量纲差异，因此在建模之前往往需要对数据进行标准化或规范化的处理，以消除数据间的量纲影响。本文主要介绍min-max规范化、z-score标准化及对数化三种常用的数据处理方法。

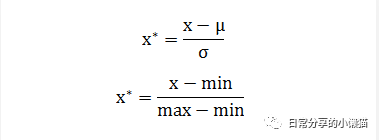
数据准备

使用R自带的mtcars数据集进行演示，选择其中的mpg,disp,hp,drat,wt, qsec等6个变量组成一个新的数据集。并且使用BruceR^[1]包进行变量的描述性统计，查看变量在均值、标准差、范围等方面所发生的变化。关于如何用BruceR输出变量描述性统计结果可参考BruceR|输出描述性统计到word三线表。

install.packages("bruceR") #安装计算变量的均值、标准差的bruceR包
data <- mtcars[c("mpg","disp","hp","drat","wt", "qsec")] #选择变量
head(data)
#                   mpg disp  hp drat    wt  qsec
#Mazda RX4         21.0  160 110 3.90 2.620 16.46
#Mazda RX4 Wag     21.0  160 110 3.90 2.875 17.02
#Datsun 710        22.8  108  93 3.85 2.320 18.61
bruceR::Describe(data) #变量描述性统计
#────────────────────────────────────────────────────────────────────────
#         N    Mean      SD  |  Median    Min     Max  Skewness  Kurtosis
#────────────────────────────────────────────────────────────────────────
#mpg     32   20.09    6.03  |   19.20  10.40   33.90      0.61     -0.37
#disp    32  230.72  123.94  |  196.30  71.10  472.00      0.38     -1.21
#hp      32  146.69   68.56  |  123.00  52.00  335.00      0.73     -0.14
#drat    32    3.60    0.53  |    3.70   2.76    4.93      0.27     -0.71
#wt      32    3.22    0.98  |    3.33   1.51    5.42      0.42     -0.02
#qsec    32   17.85    1.79  |   17.71  14.50   22.90      0.37      0.34
#────────────────────────────────────────────────────────────────────────

1、z-score标准化

z-score标准化能够根据原始数据的均值和标准差对数据进行标准化，其计算公式如下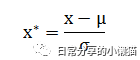：其中x为观测值，μ为均值，σ为标准差。在SPSS软件中，默认标准化的计算方法即为z-score标准化。在R中，可以利用scale() 函数对数据进行z-score标准化处理。

1.1 对数据进行z-score标准化处理

data.zscore <- scale(data) #标准化
bruceR::Describe(data.zscore) #对变量进行描述性统计
#Descriptive Statistics:
#─────────────────────────────────────────────────────────────────────
#           N   Mean    SD  |  Median    Min   Max  Skewness  Kurtosis
#─────────────────────────────────────────────────────────────────────
#X.mpg     32   0.00  1.00  |   -0.15  -1.61  2.29      0.61     -0.37
#X.disp    32  -0.00  1.00  |   -0.28  -1.29  1.95      0.38     -1.21
#X.hp      32   0.00  1.00  |   -0.35  -1.38  2.75      0.73     -0.14
#X.drat    32  -0.00  1.00  |    0.18  -1.56  2.49      0.27     -0.71
#X.wt      32   0.00  1.00  |    0.11  -1.74  2.26      0.42     -0.02
#X.qsec    32   0.00  1.00  |   -0.08  -1.87  2.83      0.37      0.34
#─────────────────────────────────────────────────────────────────────

通过Describe() 函数的输出结果可以发现，所有变量都被转为均值为0，标准差为1的数据，此外，变量的偏度、峰度并未发生变化。

1.2 将输出结果转换为数据框，并绘制变量密度曲线图

由于scale() 函数输出结果为矩阵，通常需使用as.data.frame() 函数将输出结果进一步转换为数据框，以便后续分析。

df.zscore <- as.data.frame(data.zscore) #转换为数据框
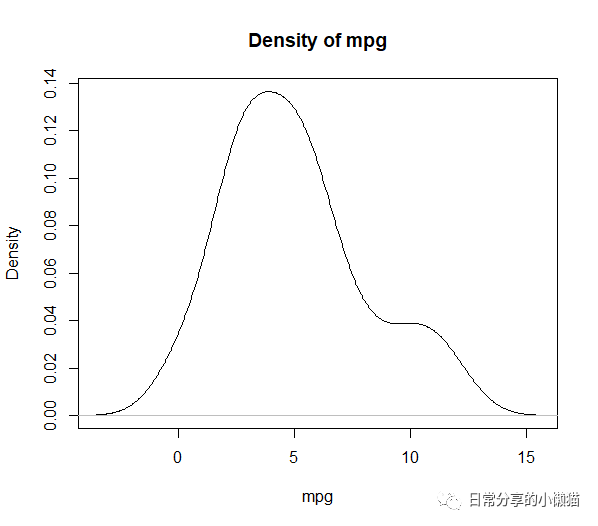
plot(density(df.user$mpg), 
     xlab = "mpg", ylab = "Density", main = "Density of mpg")#绘制变量密度图

补充：生成任意标准差与均值

此外，利用scale(data) * SD + Mean可将数据转换为任意标准差与均值样式的数据。如将演示数据转换为均值为20，标准差为10的数据。

data.user <- scale(data) * 10 + 20 #SD=10，Mean=20
bruceR::Describe(data.user) #变量描述性统计
#Descriptive Statistics:
#──────────────────────────────────────────────────────────────────────
#           N   Mean     SD  |  Median   Min    Max  Skewness  Kurtosis
#──────────────────────────────────────────────────────────────────────
#X.mpg     32  20.00  10.00  |   18.52  3.92  42.91      0.61     -0.37
#X.disp    32  20.00  10.00  |   17.22  7.12  39.47      0.38     -1.21
#X.hp      32  20.00  10.00  |   16.55  6.19  47.47      0.73     -0.14
#X.drat    32  20.00  10.00  |   21.84  4.35  44.94      0.27     -0.71
#X.wt      32  20.00  10.00  |   21.10  2.58  42.55      0.42     -0.02
#X.qsec    32  20.00  10.00  |   19.22  1.26  48.27      0.37      0.34
#──────────────────────────────────────────────────────────────────────
df.user <- as.data.frame(data.user) #转换为数据框
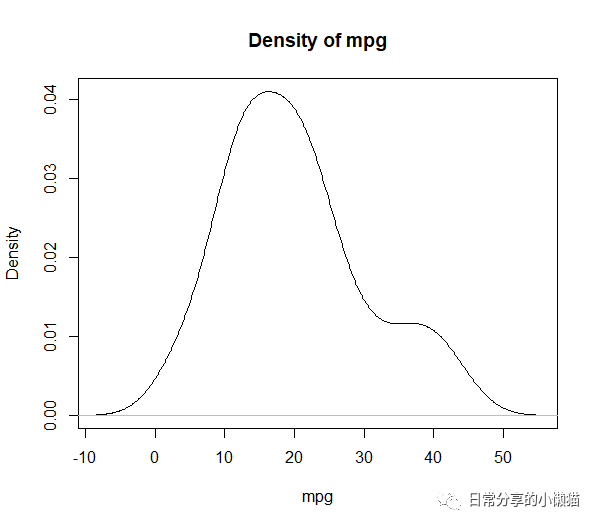
plot(density(df.user$mpg), 
     xlab = "mpg", ylab = "Density", main = "Density of mpg") #绘制变量密度图

2、min-max规范化

min-max规范化能够将数据中的观测值都转换为落在0~1范围内的数据。其计算公式如下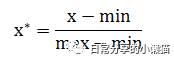：在R语言中，可以利用函数功能将min-max规范化公式定义为一个函数表达式，然后利用apply() 函数对数据框进行列操作。

2.1 对数据进行min-max规范化处理

normalization <- function(x) { return((x - min(x)) / (max(x) - min(x))) } #定义函数
data.norm <- apply(data, 2, normalization) #应用apply()函数
bruceR::Describe(data.norm) #描述性统计
#Descriptive Statistics:
#───────────────────────────────────────────────────────────────────
#           N  Mean    SD  |  Median   Min   Max  Skewness  Kurtosis
#───────────────────────────────────────────────────────────────────
#X.mpg     32  0.41  0.26  |    0.37  0.00  1.00      0.61     -0.37
#X.disp    32  0.40  0.31  |    0.31  0.00  1.00      0.38     -1.21
#X.hp      32  0.33  0.24  |    0.25  0.00  1.00      0.73     -0.14
#X.drat    32  0.39  0.25  |    0.43  0.00  1.00      0.27     -0.71
#X.wt      32  0.44  0.25  |    0.46  0.00  1.00      0.42     -0.02
#X.qsec    32  0.40  0.21  |    0.38  0.00  1.00      0.37      0.34
#───────────────────────────────────────────────────────────────────

通过以上的转换步骤，可以发现所有变量的取值范围都落在0~1范围内，变量的偏度、峰度并未发生变化。

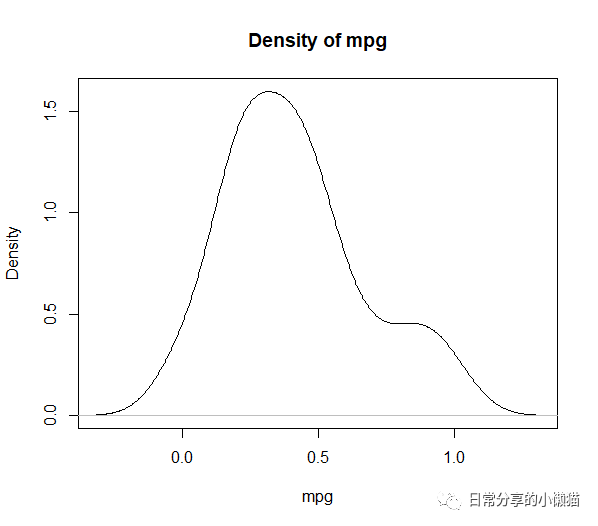
2.2 将输出结果转换为数据框，并绘制变量的密度曲线图

df.norm <- as.data.frame(data.norm) #转换为数据框
plot(density(df.norm$mpg), 
     xlab = "mpg", ylab = "Density", main = "Density of mpg") #绘制变量密度图

3、对数化处理

此外，对数化处理也是常用的变量处理方法，对数化能够让数据更加服从正态分布，在一定程度上能够消除模型异方差、降低共线性等。常用的对数变换如以自然对数为底，以10为底，以及在变量存在较多0值的情况下对变量加1再进行对数变换。在R中进行对数化处理的相关code如下：

ldata <- data #复制一份数据
head(ldata)
ldata$mpg <- log(ldata$mpg) #自然对数变换
ldata$disp <- log10(ldata$disp) #以10为底
ldata2 <- log(ldata[c("mpg", "disp", "hp", "qsec")]) #选择多个变量进行变换
ldata3 <- log(ldata) #对数据进行整体变换
ldata4 <- log(ldata$mpg + 1) #加1进行变换

附：Stata中对数化命令

Stata中对数化处理常用command如下：

import delimited "C:\Users\Acer\Desktop\mtcars.csv" //数据导入
gen lmpg = ln(mpg) //自然对数
gen lmpg10 = log10(mpg) //以10为底
gen lmpg1 = ln(mpg + 1) //加1进行变换

其他

在具体数据操作过程中，应该选择min-max规范化还是z-score标准化方法对数据进行处理，仍需要结合数据本身特点及相关参考文献对收集到的数据做进一步分析，以便确定合适的标准化方法，为数据分析打好基础。

如有帮助请多多点赞哦！

参考资料