R数据分析基础|理解数据

在进行数据分析前，首先需要对所收集到的数据进行基本探索，以便后续的数据处理与分析。本文主要分为探索数据基本结构、探索数值型变量与分类型变量以及探索变量之间的关系等4个部分，内容框架如下图所示，主要内容参考Brett Lantz的《机器学习与R语言》（third Edition）^[1]，并对部分内容进行了补充。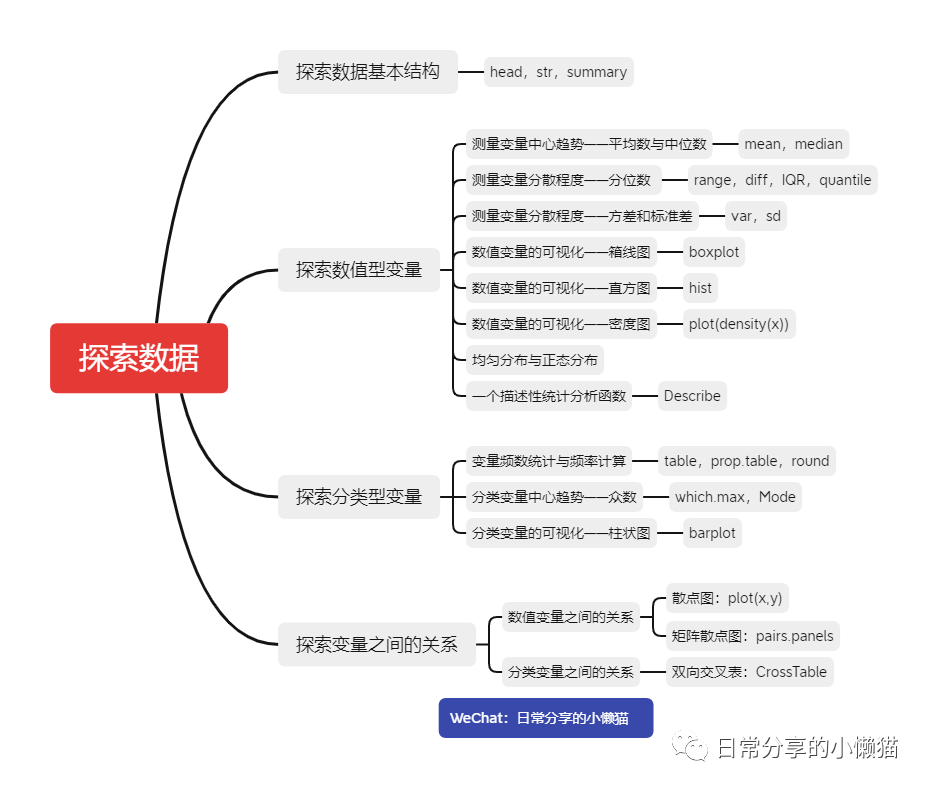

1、探索数据基本结构

探索数据基本结构通常使用head()、str()、summary() 三个基本函数。本文所使用的数据为该书所附带的数据，可在后台回复【20220218】获得。该数据为2012年在USA热门网站上发布的关于二手车打折销售广告数据，共包含7个变量。

setwd("C:\\Users\\Acer\\Desktop") #设置工作路径
usedcars <- read.csv("usedcars.csv") #读入数据
head(usedcars) #查看数据前6行
#  year model price mileage  color transmission conservative
#1 2011   SEL 21992    7413 Yellow         AUTO        FALSE
#2 2011   SEL 20995   10926   Gray         AUTO         TRUE
#3 2011   SEL 19995    7351 Silver         AUTO         TRUE
#4 2011   SEL 17809   11613   Gray         AUTO         TRUE
#5 2012    SE 17500    8367  White         AUTO         TRUE
#6 2010   SEL 17495   25125 Silver         AUTO         TRUE
str(usedcars) #了解数据基本结构，150个观测值，7个变量，以及每个变量的类型
#'data.frame': 150 obs. of  7 variables:
# $ year        : int  2011 2011 2011 2011 2012 2010 2011 2010 2011 2010 ...
# $ model       : chr  "SEL" "SEL" "SEL" "SEL" ...
# $ price       : int  21992 20995 19995 17809 17500 17495 17000 16995 16995 16995 ...
# $ mileage     : int  7413 10926 7351 11613 8367 25125 27393 21026 32655 36116 ...
# $ color       : chr  "Yellow" "Gray" "Silver" "Gray" ...
# $ transmission: chr  "AUTO" "AUTO" "AUTO" "AUTO" ...
# $ conservative: logi  FALSE TRUE TRUE TRUE TRUE TRUE ...
summary(usedcars) #对各个变量进行简单统计
#      year         model               price          mileage          color           transmission       conservative   
# Min.   :2000   Length:150         Min.   : 3800   Min.   :  4867   Length:150         Length:150         Mode :logical  
# 1st Qu.:2008   Class :character   1st Qu.:10995   1st Qu.: 27200   Class :character   Class :character   FALSE:51       
# Median :2009   Mode  :character   Median :13592   Median : 36385   Mode  :character   Mode  :character   TRUE :99       
# Mean   :2009                      Mean   :12962   Mean   : 44261                                                        
# 3rd Qu.:2010                      3rd Qu.:14904   3rd Qu.: 55125                                                        
# Max.   :2012                      Max.   :21992   Max.   :151479   

2、探索数据值型变量

2.1 测量变量中心趋势——平均数与中位数

使用mean() 与median() 函数计算变量的平均数与中位数。

mean(usedcars$price)
#[1] 12961.93
median(usedcars$price)
#[1] 13591.5

另外，使用summary() 函数的计算结果也包括平均数与中位数，此外还有变量的最大值与最小值，Q3与Q1分位所对应的数值。

summary(usedcars$price)
#   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#   3800   10995   13592   12962   14904   21992 
summary(usedcars[c("price", "mileage")])
#     price          mileage      
# Min.   : 3800   Min.   :  4867  
# 1st Qu.:10995   1st Qu.: 27200  
# Median :13592   Median : 36385  
# Mean   :12962   Mean   : 44261  
# 3rd Qu.:14904   3rd Qu.: 55125  
# Max.   :21992   Max.   :151479  

2.2 测量变量离散程度——分位数

使用range() 函数计算变量的范围；diff() 用来计算两个数值的差值；IQR() 函数用来计算变量的四分位距，即Q3-Q1；quantile() 函数可计算任意指定的分位数。

range(usedcars$price) #数据范围
#[1]  3800 21992
diff(range(usedcars$price)) #极差
#[1] 18192
IQR(usedcars$price) #四分位距：Q3-Q1
#[1] 3909.5
quantile(usedcars$price)#使用quantile()函数计算分位数
#     0%     25%     50%     75%    100% 
# 3800.0 10995.0 13591.5 14904.5 21992.0 
quantile(usedcars$price, probs = seq(from = 0, to = 1, by = 0.1))#自定义分位数
#     0%     10%     20%     30%     40%     50%     60%     70%     80%     90%    100% 
# 3800.0  8431.9 10759.4 11982.8 12993.8 13591.5 13992.0 14496.2 14999.0 15999.1 21992.0 
quantile(usedcars$price, probs = seq(0, 1, 0.1))#自定义分位数
 #    0%     10%     20%     30%     40%     50%     60%     70%     80%     90%    100% 
# 3800.0  8431.9 10759.4 11982.8 12993.8 13591.5 13992.0 14496.2 14999.0 15999.1 21992.0 
quantile(usedcars$price, probs = c(0.01, 0.99))#自定义分位数
#      1%      99% 
# 5428.69 20505.00 

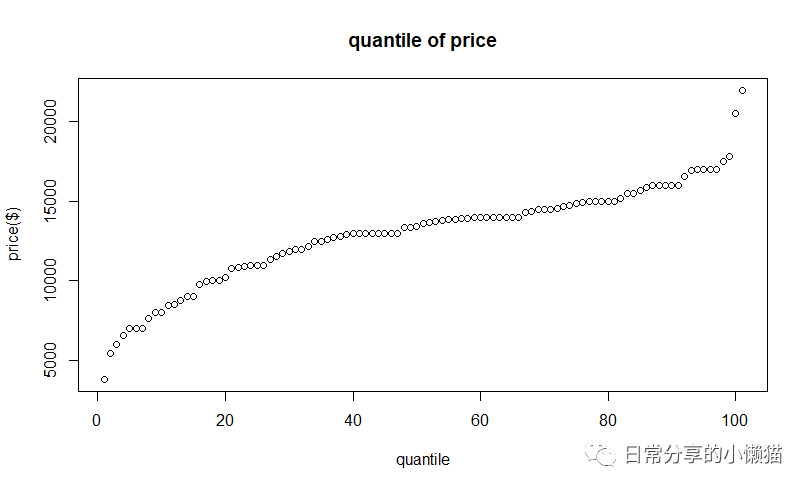
将分位数结果可视化。

df.quantile <- quantile(usedcars$price, probs = seq(0, 1, 0.01))
plot(df.quantile, 
     xlab = "quantile", ylab = "price($)", main = "quantile of price")

2.3 测量变量离散程度——方差与标准差

使用var() 与sd() 函数来计算变量的方差与标准差。

var(usedcars$price)
#[1] 9749892
sd(usedcars$price)
#[1] 3122.482

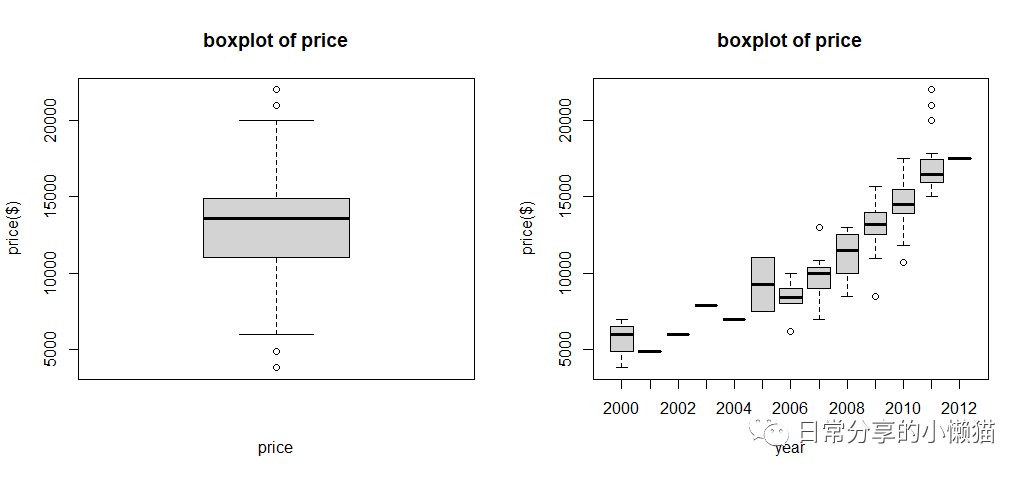
2.4 数值变量的可视化——箱线图

#单个变量箱线图，左图
boxplot(usedcars$price, xlab = "price", ylab = "price($)", main = "boxplot of price") 
#一个变量不同水平的箱线图，右图
boxplot(usedcars$price ~ usedcars$year, xlab = "year", ylab = "price($)", main = "boxplot of price")

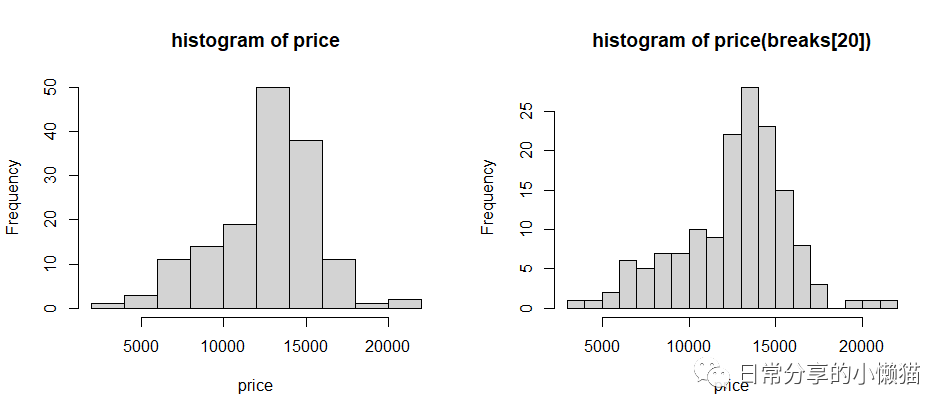
2.5 数值变量的可视化——直方图

使用hist() 函数来绘制变量的直方图。

hist(usedcars$price, xlab = "price", ylab = "Frequency", main = "histogram of price") #左图
hist(usedcars$price, breaks = 20, xlab = "price", ylab = "Frequency", main = "histogram of price(breaks[20])") #右图

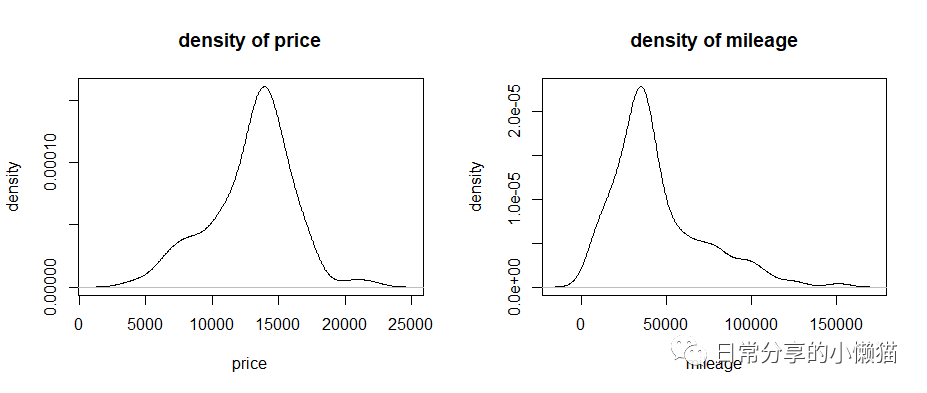
2.6 数值变量的可视化——密度图

使用plot(density(x) 函数来绘制变量的密度图。

plot(density(usedcars$price), xlab = "price", ylab = "density", main = "density of price")  #左图
plot(density(usedcars$mileage), xlab = "mileage", ylab = "density", main = "density of mileage") #右图

2.7 均匀分布与正态分布

通过对直方图及密度图的观察，可进一步分析数据的分布状况。

2.8 Describe()函数

利用bruceR^[2]中的Describe() 函数可以计算变量描述性统计结果，以探索数值型变量的基本特征。

install.packages("bruceR")
bruceR::Describe(usedcars$price)
#Descriptive Statistics:
#───────────────────────────────────────────────────────────────────────────────
#       N      Mean       SD  |    Median      Min       Max  Skewness  Kurtosis
#───────────────────────────────────────────────────────────────────────────────
#     150  12961.93  3122.48  |  13591.50  3800.00  21992.00     -0.42      0.43
#───────────────────────────────────────────────────────────────────────────────
bruceR::Describe(usedcars[c("price", "mileage")])
#Descriptive Statistics:
#───────────────────────────────────────────────────────────────────────────────────────
#             N      Mean        SD  |    Median      Min        Max  Skewness  Kurtosis
#───────────────────────────────────────────────────────────────────────────────────────
#price      150  12961.93   3122.48  |  13591.50  3800.00   21992.00     -0.42      0.43
#mileage    150  44260.65  26982.10  |  36385.00  4867.00  151479.00      1.23      1.50
#───────────────────────────────────────────────────────────────────────────────────────

3、探索分类型变量

3.1 变量频数统计与频率计算

使用table() 函数可用来统计类别变量的频次；使用prop.table() 函数可进一步计算频率分布；使用round() 函数可对统计结果的小数位进行控制。

table(usedcars$year) #year频次统计
#2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 
#   3    1    1    1    3    2    6   11   14   42   49   16    1 
table(usedcars$model) #model频次统计
# SE SEL SES 
# 78  23  49 
prop.table(table(usedcars$year)) #year频率计算
#       2000        2001        2002        2003        2004        2005        2006        2007        2008        2009 
#0.020000000 0.006666667 0.006666667 0.006666667 0.020000000 0.013333333 0.040000000 0.073333333 0.093333333 0.280000000 
#       2010        2011        2012 
#0.326666667 0.106666667 0.006666667 
round(prop.table(table(usedcars$year)) * 100, digits = 2) #乘100，保留2位小数
# 2000  2001  2002  2003  2004  2005  2006  2007  2008  2009  2010  2011  2012 
# 2.00  0.67  0.67  0.67  2.00  1.33  4.00  7.33  9.33 28.00 32.67 10.67  0.67 
round(prop.table(table(usedcars$color)) * 100, digits = 2) #乘100，保留2位小数
# Black   Blue   Gold   Gray  Green    Red Silver  White Yellow 
# 23.33  11.33   0.67  10.67   3.33  16.67  21.33  10.67   2.00 

3.2 分类变量中心趋势——众数

在对变量进行频数统计与频率计算时，频率最高的即为众数。此外，也可以使用which.max() 与prettyR包中的Mode() 函数来计算变量的众数。

which.max(table(usedcars$year))
#2010 
#  11
install.packages("prettyR")
library(prettyR)
Mode(usedcars$year)
#[1] "2010"

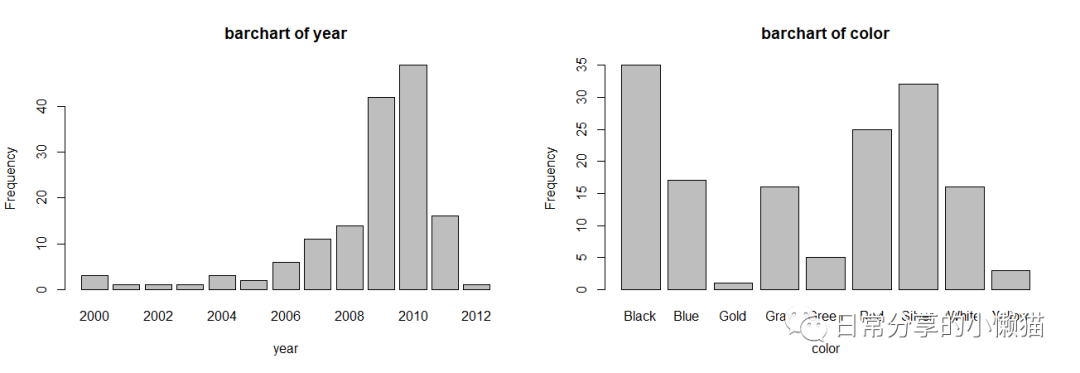
3.3 分类变量可视化——柱状图

使用barplot() 函数来绘制变量的柱状图

barplot(table(usedcars$year), xlab = "year", ylab = "Frequency", main = "barchart of year") #左图
barplot(table(usedcars$color), xlab = "color", ylab = "Frequency", main = "barchart of color") #右图

4、探索变量之间的关系

4.1 数值型变量之间的关系

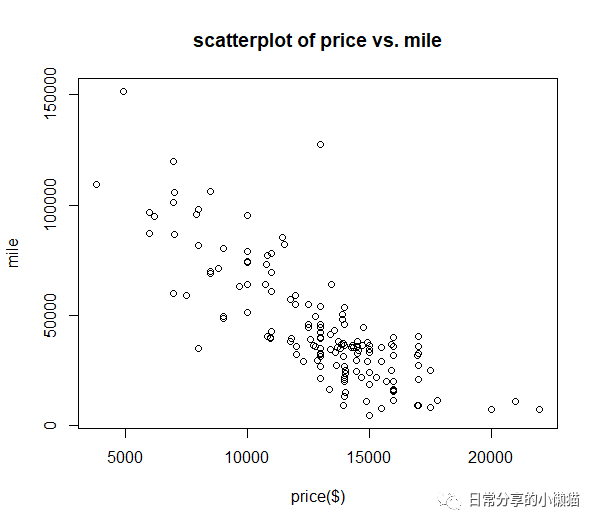
4.1.1 散点图

使用plot() 函数来绘制数值型变量间的散点图。关于如何利用ggplot2绘制散点图及添加回归拟合曲线可参考R语言绘图|散点图与回归拟合曲线。

plot(usedcars$price, usedcars$mileage, 
     xlab = "price($)", ylab = "mile", main = "scatterplot of price vs. mile")

4.1.2 散点图矩阵

关于散点图矩阵绘制的更多方法可参考R语言绘图|散点图矩阵。

#install.packages("psych")
library(psych)
pairs.panels(usedcars[c("price", "mileage")], lm = TRUE, pch = 21, stars = TRUE, ci = TRUE)

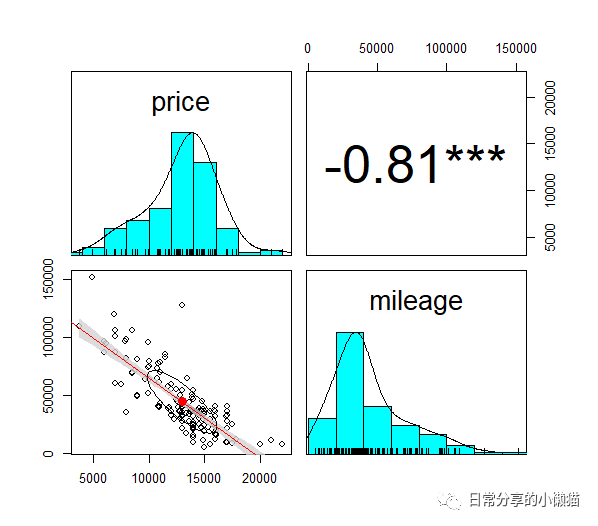
4.2 分类型变量之间的关系

检验model和color两个分类变量间的关系。将color变量分为两组（是否为保守颜色），第一组保守颜色包括Black、Gray、Silver、White，其余颜色为第二组非保守颜色，使用 %in% 运算符来创建一个二元变量conservative（虚拟变量）， %in% 运算符会返回一个TRUE或者FALSE结果。

#install.packages("gmodels")
library(gmodels)
table(usedcars$color)
# Black   Blue   Gold   Gray  Green    Red Silver  White Yellow 
#    35     17      1     16      5     25     32     16      3 
usedcars$conservative <- usedcars$color %in% c("Black", "Gray", "Silver", "White")
table(usedcars$conservative)
#FALSE  TRUE 
#   51    99 

利用table() 函数生成列联表。

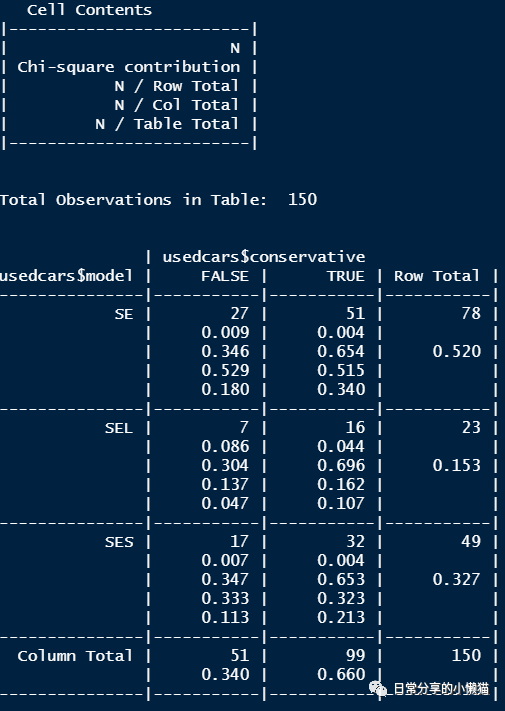
table(usedcars$model, usedcars$conservative) #列联表
#      FALSE TRUE
#  SE     27   51
#  SEL     7   16
#  SES    17   32

利用CrossTable() 函数进行列联表检验。结果包括观测值数量、卡方统计量、行占比、列占比及整体占比。

CrossTable(usedcars$model, usedcars$conservative)

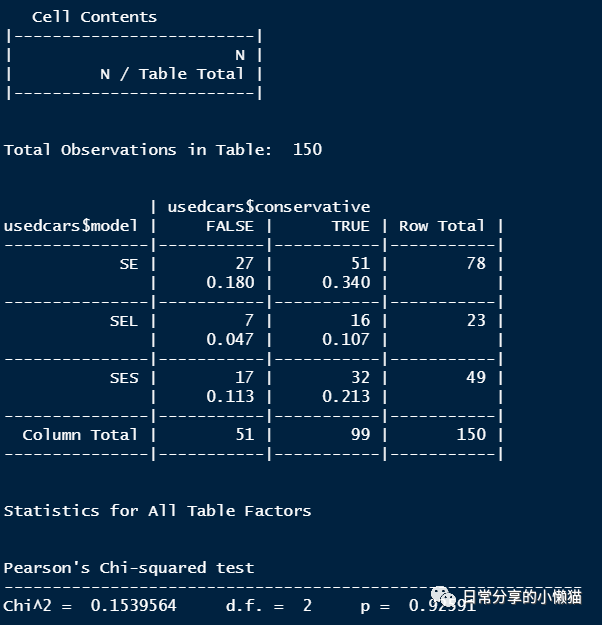
对CrossTable() 函数内的参数进一步调整。

CrossTable(usedcars$model, usedcars$conservative, prop.r = FALSE, prop.c = FALSE, prop.chisq = FALSE, chisq = TRUE) 

其他

本章为Brett Lantz的Machine Learning with R中的基础数据管理与理解章节，后续将进一步介绍该书中的相关机器学习算法与模型。

如有帮助请多多点赞哦！

参考资料