
前面我们已经介绍了如何找出合格的关联规则。
我们知道在计算关联规则的时候,需要首先遍历所有的项集,判断是否是频繁项集,然后计算所有的频繁项集两两之间的置信度。假使一共有个项,产生的项集有个,假使其中频繁项集的比例为,则需要计算次置信度。显然这个计算量会非常大。有没有什么方法能够尽量简化计算量呢?
这就要提到我们即将介绍的apriori算法。事实上,该算法主要是基于频繁项集的两个性质对频繁项集的计算过程进行剪枝。
性质1:频繁项集的子集一定是频繁项集
性质2:非频繁项集的超集一定是非频繁项集

| 订单号 | 订单内容 |
|---|---|
001 | A,C,D |
002 | B,C,E |
003 | A,B,C,E |
004 | B,E |
005 | A,B,C |
给定最小支持度阈值,最小置信度阈值,找出以上购物篮的所有合格的关联规则。
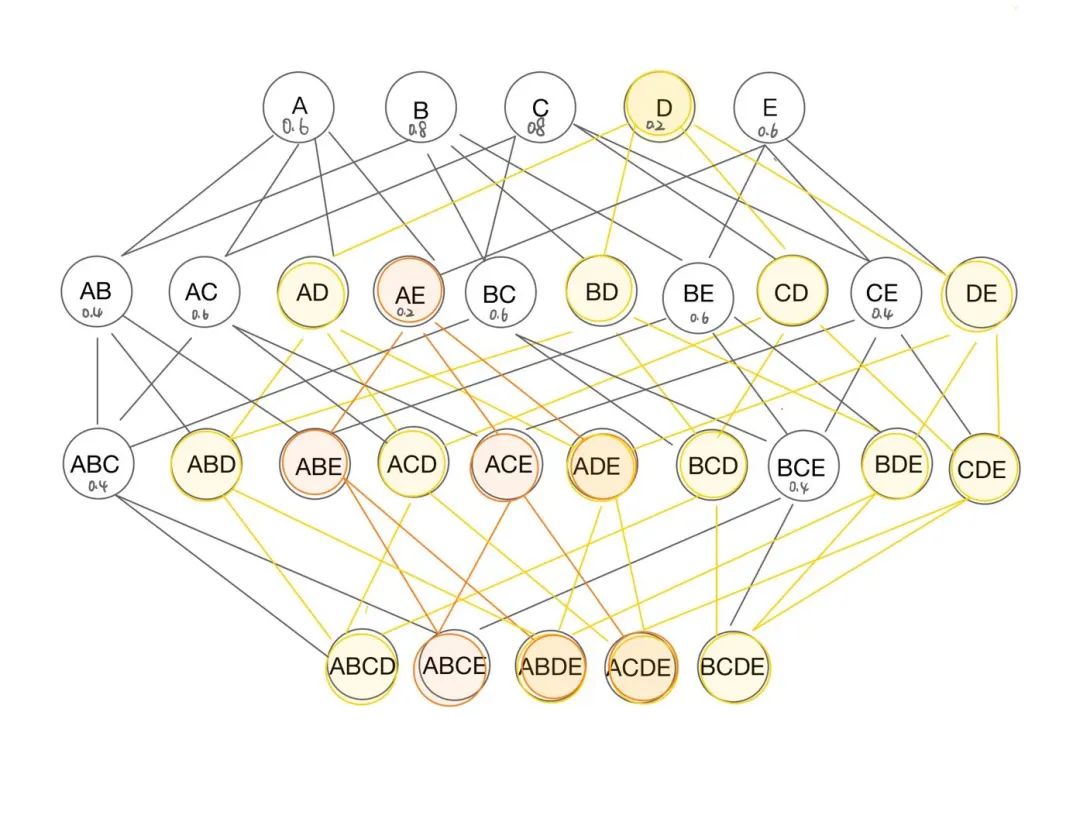
第一步:计算出所有的频繁项集
| 1-项集 | 支持度 | 2-项集 | 支持度 | 3-项集 | 支持度 |
|---|---|---|---|---|---|
| A | 0.6 | AB | 0.4 | ABC | 0.4 |
| B | 0.8 | AC | 0.6 | BCE | 0.4 |
| C | 0.8 | AE | 0.2 | ||
| D | 0.2 | BC | 0.6 | ||
| E | 0.6 | BE | 0.6 | ||
| CE | 0.4 |
第二步:计算出频繁项集之间的置信度
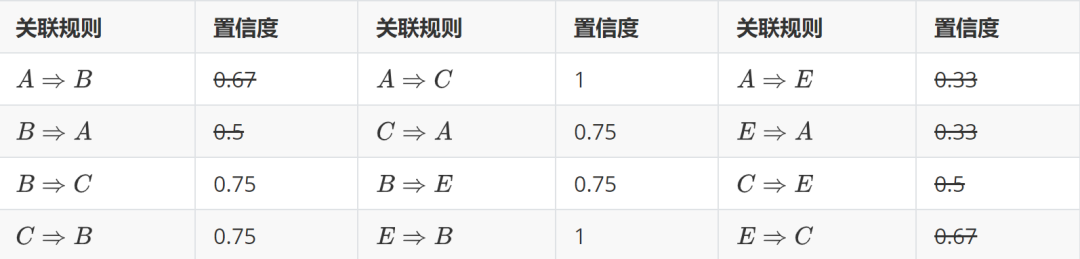
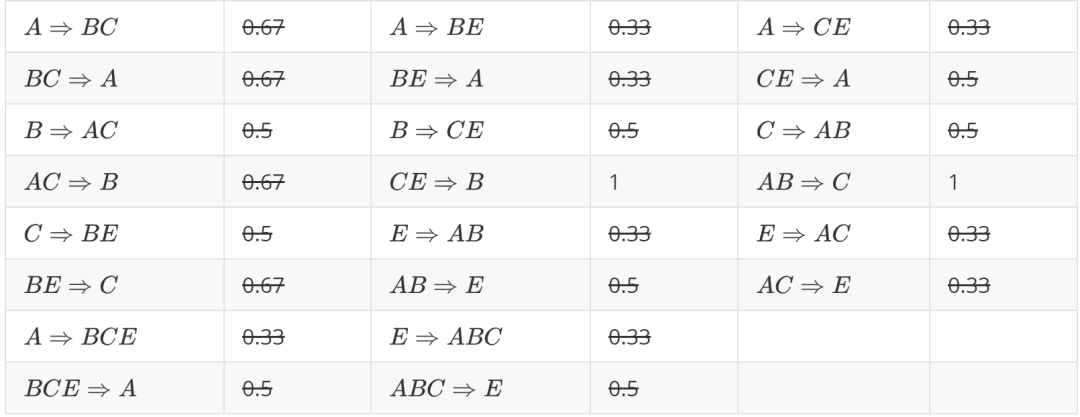


提升度 : 我们在做商品推荐或者风控策略的时候,重点考虑的是提升度,因为提升度代表的是A 的出现,对B的出现概率提升的程度。
所以提升度有三种可能:
:说明规则的效果比直接基于数据项频率的猜测更好,有兴趣性。
:说明前项与后项相互独立(独立事件的概率等式),规则的效果与直接基于数据项频率的猜测相同,没有兴趣性;;
:说明规则的效果比直接基于数据项频率的猜测更差,无兴趣性。
使用提升度对前面8条合格关联规则进行剪枝,有3条关联规则的提升度小于1,可以删去
杠杆度:杠杆度与提升度类似,反映关联规则前项与后项之间的关系
如果杠杆度等于0,前项与后项之间独立;杠杆度越大,前项与后项之间的关系越紧密。

进行关联规则分析的时候,这里我们使用akapriori第三方库。Github相关资源标题为:GitHub - aknd/akapriori: Python implementation of the Apriori Algorithm.
from akapriori import apriori
dataset = [[‘A’,’C’,’D’],[‘B’,’C’,’E’],[‘A’,’B’,’C’,’E‘],[‘B’,’E’],[‘A’,’B’,’C’]]
rules = apriori(dataset, support = 0.4, confidence = 0.7, lift = 0)
for i in rules:
print(i)

图二 akapriori库当中的apriori函数定义
apriori函数参数使用说明:
transcations: #要计算的数据集
support:#自定义的支持度,默认值为0.1
confidence:#自定义的置信度,默认值为0.8
lift:#自定义的提升度,默认值为1
minlen:#关联规则包含的最短的项数,默认为2
maxlen:#关联规则包含的最长的项数,默认为2
运行结果如下
(frozenset({'C'}), frozenset({'B'}), 0.6, 0.75, 0.9375)
(frozenset({'B'}), frozenset({'C'}), 0.6, 0.75, 0.9375)
(frozenset({'E'}), frozenset({'B'}), 0.6, 1.0, 1.25)
(frozenset({'B'}), frozenset({'E'}), 0.6, 0.75, 1.25)
(frozenset({'C'}), frozenset({'A'}), 0.6, 0.75, 1.25)
(frozenset({'A'}), frozenset({'C'}), 0.6, 1.0, 1.25)







