以下文章来源于labuladong ,作者labuladong
题目分析
重复一下题目的本质:
给你输入若干时间区间,让你计算同一时刻「最多」有几个区间重叠。
题目的关键点在于,给你任意一个时刻,你是否能够说出这个时刻有几个会议在同时进行?
如果可以做到,那我遍历所有的时刻,找个最大值,就是需要申请的会议室数量。
有没有一种数据结构或者算法,给我输入若干区间,我能知道每个位置有多少个区间重叠?
老读者肯定可以联想到之前说过的一个算法技巧:差分数组技巧。
把时间线想象成一个初始值为 0 的数组,每个时间区间[i, j]就相当于一个子数组,这个时间区间有一个会议,那我就把这个子数组中的元素都加一。
最后,每个时刻有几个会议我不就知道了吗?我遍历整个数组,不就知道至少需要几间会议室了吗?
举例来说,如果输入meetings = [[0,30],[5,10],[15,20]],那么我们就给数组中[0,30],[5,10],[15,20]这几个索引区间分别加一,最后遍历数组,求个最大值就行了。
还记得吗,差分数组技巧可以在 O(1) 时间对整个区间的元素进行加减,所以可以拿来解决这道题。
不过,这个解法的效率不算高,所以我这里不准备具体写差分数组的解法,参照 差分数组技巧 的原理,有兴趣的读者可以自己尝试去实现。
基于差分数组的思路,我们可以推导出一种更高效,更优雅的解法。
我们首先把这些会议的时间区间进行投影:
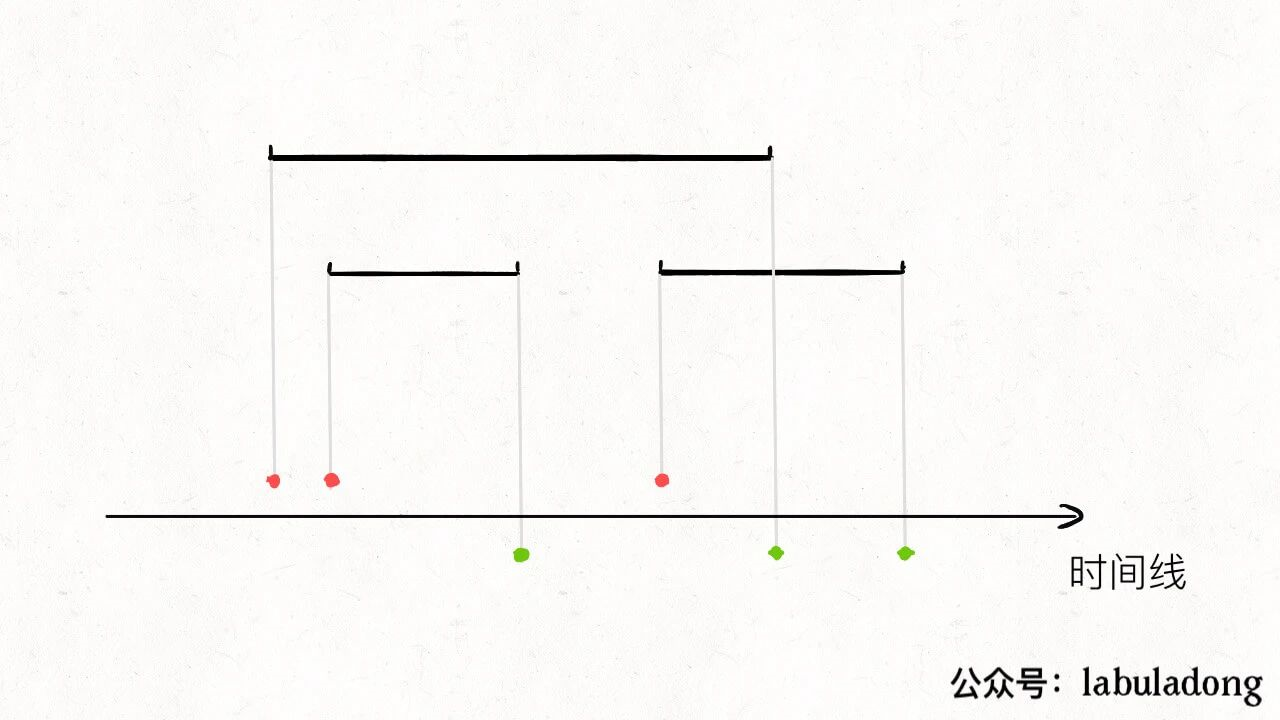
红色的点代表每个会议的开始时间点,绿色的点代表每个会议的结束时间点。
现在假想有一条带着计数器的线,在时间线上从左至右进行扫描,每遇到红色的点,计数器count加一,每遇到绿色的点,计数器count减一:
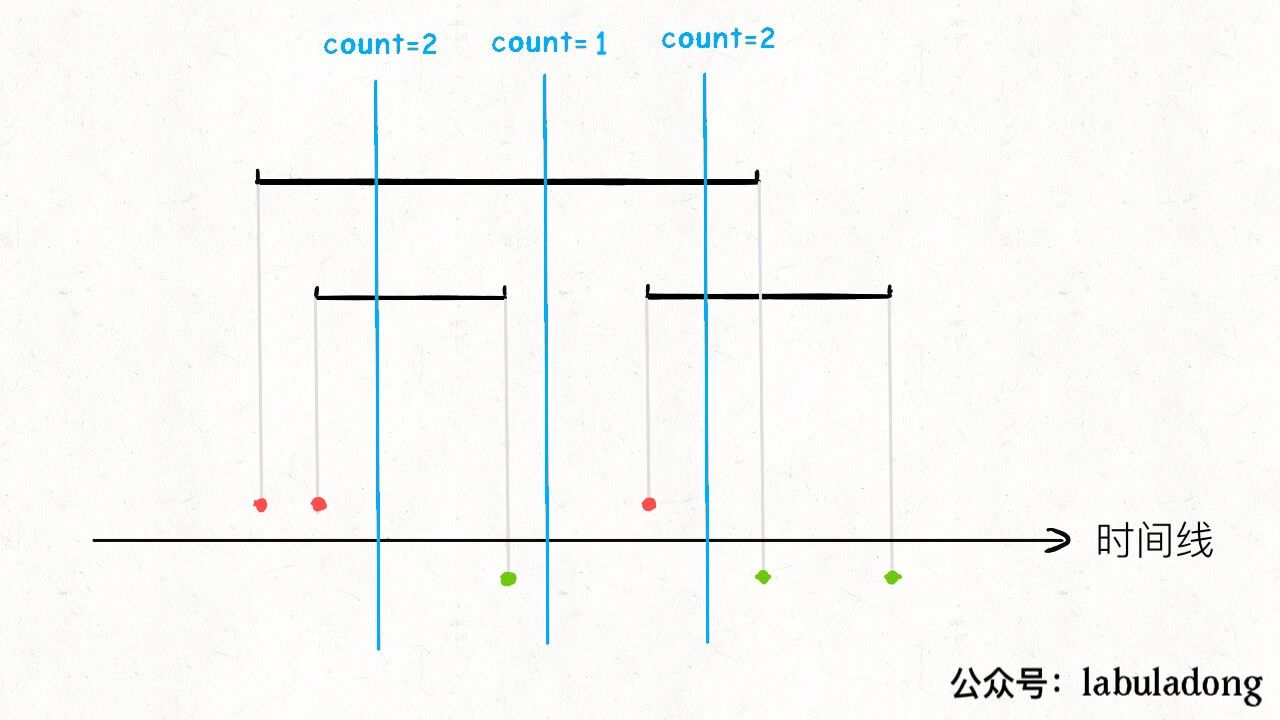
这样一来,每个时刻有多少个会议在同时进行,就是计数器count的值,count的最大值,就是需要申请的会议室数量。
对差分数组技巧熟悉的读者一眼就能看出来了,这个扫描线其实就是差分数组的遍历过程,所以我们说这是差分数组技巧衍生出来的解法。
代码实现
那么,如何写代码实现这个扫描的过程呢?
首先,对区间进行投影,就相当于对每个区间的起点和终点分别进行排序:
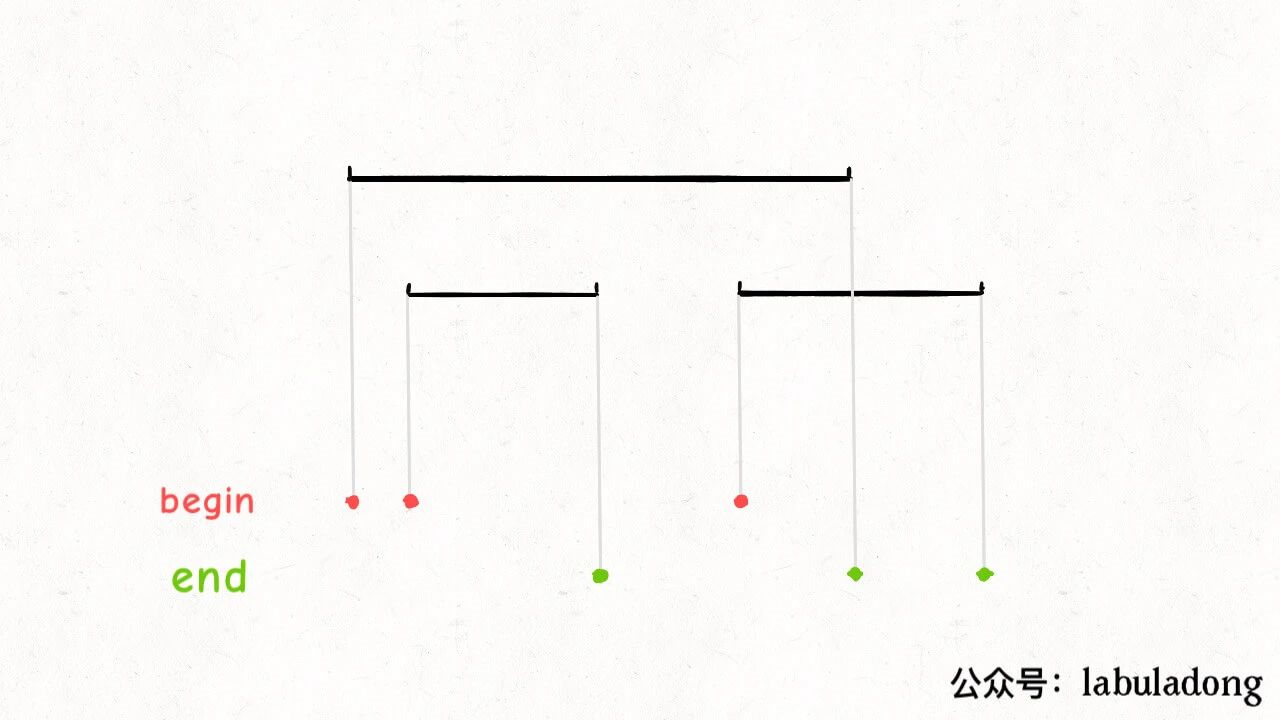
int minMeetingRooms(int[][] meetings) {
int n = meetings.length;
int[] begin = new int[n];
int[] end = new int[n];
// 把左端点和右端点单独拿出来
for(int i = 0; i < n; i++) {
begin[i] = meetings[i][0];
end[i] = meetings[i][1];
}
// 排序后就是图中的红点
Arrays.sort(begin);
// 排序后就是图中的绿点
Arrays.sort(end);
// ...
}
然后就简单了,扫描线从左向右前进,遇到红点就对计数器加一,遇到绿点就对计数器减一,计数器count的最大值就是答案:
int minMeetingRooms(int[][] meetings) {
int n = meetings.length;
int[] begin = new int[n];
int[] end = new int[n];
for(int i = 0; i < n; i++) {
begin[i] = meetings[i][0];
end[i] = meetings[i][1];
}
Arrays.sort(begin);
Arrays.sort(end);
// 扫描过程中的计数器
int count = 0;
// 双指针技巧
int res = 0, i = 0, j = 0;
while (i < n && j < n) {
if (begin[i] < end[j]) {
// 扫描到一个红点
count++;
i++;
} else {
// 扫描到一个绿点
count--;
j++;
}
// 记录扫描过程中的最大值
res = Math.max(res, count);
}
return res;
}
这里使用的是 双指针技巧,你可以认为指针 i 就是那根扫描线,根据i, j的相对位置就可以模拟扫描线前进的过程。
至此,这道题就做完了。当然,这个题目也可以变形,比如给你若干会议,问你k个会议室够不够用,其实你套用本文的解法代码,也可以很轻松解决。






