

长按二维码关注
大数据领域必关注的公众号

文末扫描二维码免费获取《大数据算法面试文档》
题目描述:
有一个GB大小的文件,文件里面每一行是一个英文单词,每个单词的大小不超过16个字节,内存限制是1MB。请设计一个算法思路,返回单词词频数最高的100个单词(Top100)。
题目解析:
题目中文件的大小为1GB,由于内存大小的限制,我们无法直接将这个大文件的所有单词一次性读入内存中。因此我们需要采用分治法,将一个大文件分割成若干个小文件,并且每个小文件的大小不超过1MB,从而能将每个小文件分别加载到内存中进行处理。然后使用HashMap分别统计出每个小文件的单词词频数,并获取每个小文件词频最高的100个单词。最后使用小顶堆统计出所有单词中出现词频最高的100个单词。
实现方式:分治法
步骤1
首先遍历这个大文件,对文件中遍历到的每个单词word,执行n=hash(word)%5000操作,然后将结果为n的单词存放到第fn个文件中。整个大文件遍历结束之后,我们可以得到5000个小文件,每个小文件的大小为200KB左右。如果有的小文件的大小仍然超过1MB,则采用同样的方式继续进行分解,直到每个小文件的大小都小于1MB为止。文件分割过程如图1-1所示。
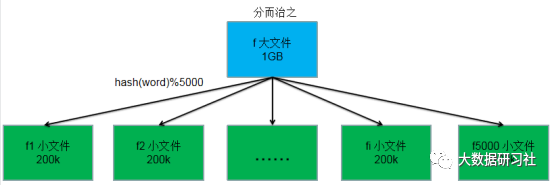
图1-1 文件分割过程
步骤2
分别统计每个小文件中出现单词词频数最高的100个单词,最简单的实现方式是使用HashMap来实现,其中key为单词,value为该单词出现的词频数。具体做法是:遍历文件中的所有单词,对于遍历到的单词word,如果word在map中不存在,那么就执行map.put(word,1),将该词频设置为1;如果word在map中存在,那么就执行map.put(word,map.get(word)+1),将该单词词频数加1。遍历完成之后,可以很容易找出每个文件出现频率最高的100个单词。词频统计逻辑如图1-1所示。
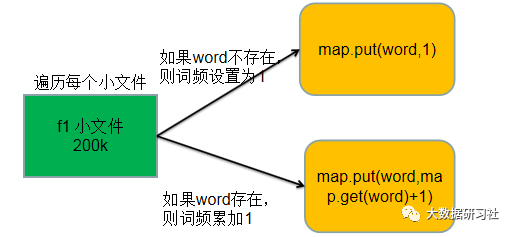
图1-1词频统计逻辑
步骤3
因为步骤2已经找出了每个文件出现频率最高的100个单词,接下来我们可以通过维护一个小顶堆来找出所有单词中出现频率最高的100个单词。具体做法是:依次遍历每个小文件,构建一个小顶堆,堆大小为100。如果遍历到的单词出现的次数大于堆顶单词出现的次数,那么就用新单词替换堆顶的单词,然后重新调整为小顶堆。当遍历完所有文件后,小顶堆中的单词就是出现频率最高的100个单词。小顶堆构建过程如图1-1所示。
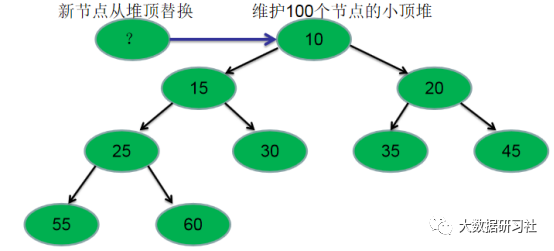
如图1-1 小顶堆构建过程
方法总结:
针对限定内存,求解海量数据的TopN问题,可以采取以下几个步骤。
1.分而治之,利用哈希取余,将大文件分割为小文件。
2.使用HashMap统计每个单词的词频。
3.求解词频最大的TopN,使用小顶堆;求解词频最小的TopN,使用大顶堆。
题目描述:
现在有一个1亿条记录的超大文件,里面包含着某一天海量用户访问日志,但已有内存存放不下该文件,现要求从这个超大文件中统计出某天访问百度次数最多的那个IP地址。
题目解析:
因为题目中只关心访问百度最多的IP地址,所以需要对原始文件进行遍历,将这一天访问百度的IP的相关记录输出到一个单独的大文件中。由于内存大小的限制,我们无法将这个大文件一次性加载到内存中,所以需要采用分治法将大文件分割为若干个小文件,直到内存可以装下每个小文件为止。然后使用HashMap分别统计出每个小文件中的每个IP地址出现的次数,并找出每个小文件中出现次数最多的IP地址。最后比较所有小文件中出现次数最多的IP,从而最终统计出这个超大文件中访问百度最多的IP地址。
实现方式:分治法
步骤1
首先遍历超大原始日志文件,将包含百度url地址的相关信息记录输出到一个单独的大文件中,那么这个新生成的大文件只包含访问百度的相关信息记录。文件过滤如图1-1所示。

图1-1 文件过滤
步骤2
然后遍历新生成的大文件,对文件中遍历到的每个IP执行n=hash(IP)%1000操作,将结果为n的日志记录放到第fn个文件中。整个大文件遍历结束后,我们可以得到1000个小文件。那么相同的IP会存储到同一个文件中,分割后的每个小文件的大小为大文件的1/1000。如果分割后的文件中仍然有部分文件无法装载到内存中,可以对该文件进行分割直至内存可以装下为止。文件分割过程如图1-1所示。
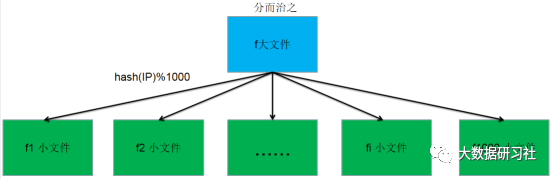
如图1-1 文件分割过程
步骤3
接着统计每个小文件中出现次数最多的IP,最简单的方法是通过HashMap来实现,其中key为IP地址,value为该IP地址出现的次数。具体做法是:遍历每个小文件中的所有记录,对于遍历到的IP,如果IP地址在map中不存在,那么就执行map.put(IP,1),将该IP出现次数设置为1;如果IP地址在map中存在,那么就执行map.put(IP,map.get(IP)+1),将该IP出现的次数加1。然后再遍历HashMap,可以很容易分别统计出每个文件中访问百度次数做多的IP。IP访问次数统计逻辑如图1-1所示。
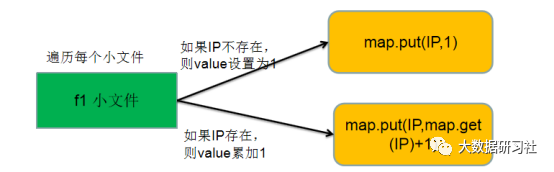
如图1-1 IP访问次数统计逻辑
步骤4
最后比较所有小文件中访问百度次数最多的IP,便可以统计出整个超大文件中某日访问百度次数最多的IP地址。结果汇总过程如图1-1所示
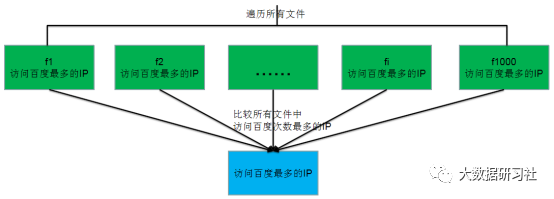
如图1-1 结果汇总过程
方法总结:
针对限定内存,求解海量数据的最大值问题,可以采取以下几个步骤。
1.分而治之,利用哈希取余,将大文件分割为小文件。
2.使用HashMap统计每个IP出现的次数。
3.求解IP出现次数的最大值,遍历HashMap即可。
题目描述:
在2.5亿个整数文件中找出不重复的整数。
备注:现有内存无法容纳2.5亿个整数。
题目解析:
题目中已经说明现有内存无法容纳2.5亿个整数,所以我们无法一次性将所有数据加载到内存中进行处理。
实现方式1:分治法
由于无法直接将2.5亿个整数一次性加载到内存处理,所以我们需要采用分治法,将一个大文件分割成若干个小文件,从而能将每个小文件分别加载到内存中进行处理,然后使用HashMap分别统计出每个小文件中每个整数出现的次数,最后遍历HashMap输出value值为1的整数即可。
步骤1
首先遍历这个大文件,对文件中遍历到的每个整数digit执行hash(digit)%1000操作,将结果为n的整数存放到第fn个文件中。整个大文件遍历结束之后,我们就可以将2.5亿个整数划分到1000个小文件中。那么相同的整数会存储到同一个文件中,分割后的每个小文件的大小为大文件的1/1000。如果有的小文件仍然无法加载到内存中,则可以采用同样的方式继续进分解,直到每个小文件都可以加载到内存中为止。文件分割过程如图1-1所示。
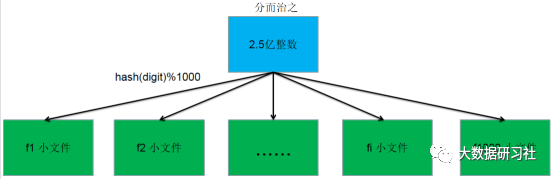
如图1-1 文件分割过程
步骤2
然后在每个小文件中找出不重复的整数,最简单的方法是通过HashMap来实现,其中key为整数,value为该整数出现的次数。具体做法是:遍历每个小文件中的所有记录,对于遍历到的整数digit,如果digit在map中不存在,那么就执行map.put(digit,1),将digit出现次数设置为1;如果digit在map中存在,那么就执行map.put(digit,map.get(digit)+1),将digit出现的次数加1。整数出现次数统计逻辑如图1-1所示。
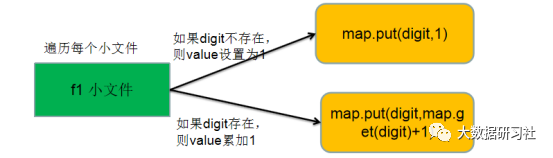
如图1-1 整数出现次数统计逻辑
步骤3
最后针对每个小文件,遍历HashMap输出value为1的所有整数,就可以找出这2.5亿个整数中所有的不重复的数。这里不用再对每个小文件输出的整数进行重复筛重,因为每个整数经过hash函数处理后,相同的整数只会被划分到同一个小文件中,不同的文件中不会出现重复的整数。
实现方式2:位图法
对于整数相关的算法的求解,位图法是一种非常实用的算法。假设整数占用4B,即32bit,那么可以表示的整数的个数为2^32。那么对于本题目来说,我们只需要查找不重复的数,而无需关心具体整数出现的次数,所以可以分别使用2个bit来表示各个数字的状态:00表示这个数字没有出现过;01表示这个数字出现过一次;10表示这个数字出现过多次。那么这2^32个整数,总共需要的内存为2^32*2b=1GB。因此,当可用内存超过1GB时,可以采用位图法求解该题目。
步骤1
首先需要开辟一个用2Bitmap法标志的2^32个整数的桶数组,并初始化标记位为00,其存储的数据量远远大于2.5亿个整数。开辟并初始化位图如图1-1所示。

如图1-1开辟并初始化位图
步骤2
然后遍历2.5亿个整数,并查看每个整数在位图中对应的位,如果位值为00,则修改为01,如果位值为01,则修改为10,如果位值为10则保持不变。遍历数据并修改位图状态如图1-1所示。
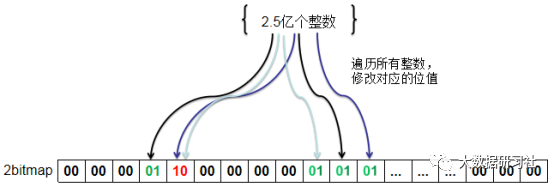
如图1-1 遍历数据并修改位图状态
步骤3
最后当所有数据都遍历完成之后,可以再遍历一遍位图,把对应位值是01的整数输出,即可统计出2.5亿个整数中所有不重复的数。
方法总结:
判断整数是否重复的问题,位图法是一种非常高效的方法,当然前提是:内存要满足位图法所需要的存储空间。
题目描述:
给定40亿个不重复的没有排序过的整数,然后再给定一个整数,如何快速判断这个整数是否包含在这40亿个整数当中。备注:现有内存不足以容纳这40亿个整数。
题目解析:
题目中已经说明现有内存无法容纳40亿个整数,所以我们无法一次性将所有数据加载到内存中进行处理,那么最容易想到的方法还是分治法。
实现方式1:分治法
根据实际内存大小情况,确定一个hash函数,比如hash(digit)%1000,通过这个hash函数将40亿个整数划分到若干个小文件(f1,f2,f3,...,f1000),从而确保每个小文件都能加载到内存中进行处理。然后再对待找出的整数使用相同的hash函数求出hash值,假设计算出的这个hash值为n,如果这个整数存在的话,那么它一定存在fn文件中。接着将fn文件中所有的整数都保存到HashSet中,最后判断待查找的整数是否存在。由于详细步骤与前面分治法类似,这里就不再赘述了。
实现方式2:位图法
假设整数占用4B,即32bit,那么可以表示的整数的个数为2^32。那么对于本题目来说,我们只需要判断整数是否存在,而无需关心整数出现的次数,所以可以使用1个bit来标记整数是否存在:0表示这个整数不存在;1表示这个整数存在。那么这2^32个整数,总共需要的内存为2^32*2b=1GB。因此,当可用内存超过1GB时,可以采用位图法求解该题目。
步骤1
首先需要开辟一个用1Bitmap法标志的2^32个整数的桶数组,并初始化标记位为0,其存储的数据量大于40亿个整数。开辟并初始化位图如图1-1所示。
如图1-1开辟并初始化位图
步骤2
然后遍历40亿个整数,将对应的位值设置为1。遍历数据并修改位图状态如图1-1所示。
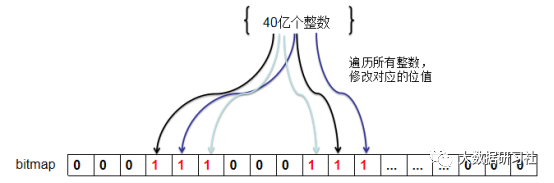
如图1-1 遍历数据并修改位图状态
步骤3
最后再读取要查询的整数,查看对应的位值是否为1,如果位值为1表示存在,如果位值为0表示不存在。
方法总结:
判断数字是否存在、判断数字是否重复的问题,位图法是一种非常高效的方法。
题目描述:
CSDN网站搜索引擎会通过日志文件把用户每次搜索使用关键词都记录下来,每个查询关键词限定长度为1~255个字节。假设目前有1000万个搜索记录,现要求统计最热门的10个搜索关键词。备注:现有内存不超过1GB。
题目解析:
从题目中给出的信息可知,每个搜索关键词最长为255个字节,1000万个搜索记录需要占用约10000000*255B≈2.55GB内存,因此,我们无法将所有搜索记录全部读入内存中处理。
实现方式1:分治法
分治法依然是一个非常实用的方法。首先将整个搜索记录文件分割为多个小文件,保证单个小文件中的搜索记录可以全部加载到内存中处理,然后统计出每个小文件中出现次数最多的10个搜索关键词,最后设计一个小顶堆统计出所有文件中出现最多的10个搜索关键词。在本题目中,分治法虽然可行,但不是最好的方法,因为需要2次遍历文件,分割文件的Hash函数被调用1000万次,所以性能不是很好,这里就不再赘述。
实现方式2:HashMap法
虽然题目中搜索关键词的总数比较多,但是一般关键词的重复度比较高,去重之后搜索关键词不超过300万个,因此可以考虑把所有搜索关键词及出现的次数保存到HashMap中,由于存储次数的整数一般占用4个字节,所以HashMap所需要占用的空间为300万*(255+4)≈800M,因此题目中限定的1GB内存完全够用。
步骤1
首先遍历所有搜索关键词,如果关键词存在与map中,则value值累加1;如果关键词不在map中,则value值设置为1。关键词出现次数统计逻辑如图1-1所示。
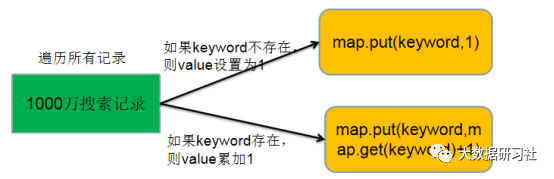
如图1-1 关键词出现次数统计逻辑
步骤2
然后遍历map集合,构建一个包含10个元素的小顶堆,如果遍历到的关键词出现的次数大于堆顶关键词出现的次数,则进行替换,并将堆调整为小顶堆。小顶堆构建过程如图1-1所示。
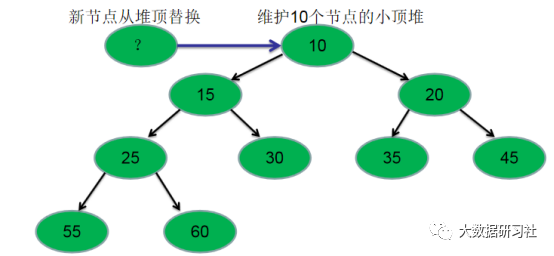
图1-1 小顶堆构建过程
步骤3
最后直接取出堆中的10个关键词就是出现次数最多的字符串。
实现方式3:前缀树法
前缀树:又称为字典树、单词查找树,是一种哈希树的变种。典型应用是用于统计、排序和保存大量的字符串,所以经常被搜索引擎系统用于文本词频统计。
实现方式2使用了HashMap来统计关键词出现的次数,当这些关键词有大量相同的前缀时,可以考虑使用前缀树来统计搜索关键词出现的次数,树的结点可以保存关键词出现的次数。
步骤1
首先遍历所有搜索关键词,针对每个关键词在前缀树中查找,如果能找到,则把结点中保存的关键词次数加1,否则就为这个关键词构建新的结点,构建完成之后把叶子结点中关键词的出现次数设置为1。当遍历完所有关键词之后,就可以知道每个关键词的出现次数了。前缀树的构建过程如图1-1所示。
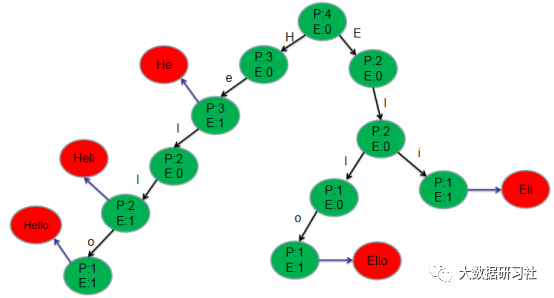
如图1-1 前缀树的构建过程
备注:每个结点中的P表示所有字符添加到树的过程中,这个结点到达过几次,E表示当前结点有多少个字符串是以它结尾。
步骤2
然后遍历前缀树,就可以找出出现次数最多的关键词。
方法总结:
前缀树经常被用来统计字符串的出现次数,它的另外一个用途是字符串查找,判断是否有重复的字符串等。
题目描述:
已知某个文件内包含海量的电话号码,每个号码为8位数字,要求统计有多少个不同的电话号码。
题目解析:
这类题目其实就是求解数据重复的问题,一般来说,对于这类问题首先会考虑使用位图法处理。就本题目而言,8位电话号码的范围为00000000~99999999,那么可以表示的电话号码个数为10^8,即1亿个。如果用1bit表示一个号码,那么总共需要1亿个bit,大约占用100M的内存。
实现方式:位图法
步骤1
首先需要开辟一个用1Bitmap法标记的1亿个整数的桶数组,并初始化标记位为0。开辟并初始化位图如图1-1所示。

如图1-1开辟并初始化位图
步骤2
然后遍历所有电话号码,将电话号码对应的位值设置为1。遍历完成之后,如果对应的位值为1,则表示这个电话号码在文件中存在,否则表示电话号码不存在。遍历数据并修改位图状态如图1-1所示。
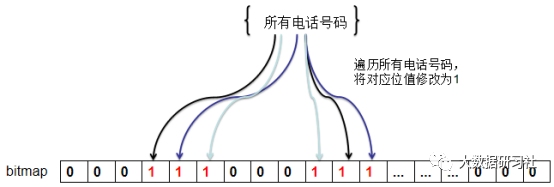
如图1-1 遍历数据并修改位图状态
步骤3
最后再遍历一遍位图,统计位值为1的数量即为不同电话号码的个数。
方法总结:
求解数据重复问题,在内存有限的情况下,一般选择使用位图法。
题目描述:
腾讯面试:给定内存500k,现在有一百万条查询数据,每条数据20B,现要求找出重复次数最多的那一条数据。
题目解析:
题目中每条数据大小为20B,一共有一百万条查询记录,那么数据总大小为约为1000000*20B≈20M,由于给定内存限制为500k,所以我们无法直接一次性加载所有查询数据到内存。因此我们需要采用分治法,将一百万条查询数据使用hash函数分割为100个小文件,每个小文件大约占用内存200k,同时相同的字符串会存储在同一个文件中。然后使用HashMap分别统计出每个小文件中相同字符串的个数,并找出字符串出现次数做多的100个。最后遍历每个小文件中出现次数最多的100个字符串,只需要使用一个变量即可统计出重复次数最多的字符串。
实现方式:分治法
步骤1
首先遍历一百万条查询数据,对每条查询记录的字符串str,执行n=hash(str)%100操作,然后将结果为n的字符串存放到第fn个文件中。所有数据遍历结束之后,我们可以得到100个小文件,每个小文件的大小为200KB左右。如果部分小文件的大小仍然超过500k,则采用同样的方式继续进行分解,直到每个小文件的大小都小于500k为止。文件分割过程如图1-1所示。
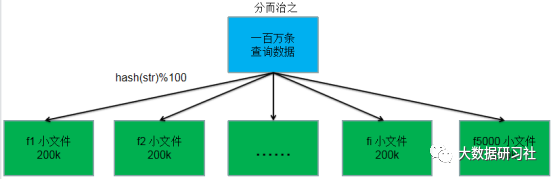
图1-1 文件分割过程
步骤2
统计每个小文件中出现次数最多的100个字符串,最简单的实现方式是使用HashMap来实现,其中key为字符串,value为该字符串出现的次数。具体做法是:遍历文件中的所有字符串,对于遍历到的字符串str,如果str在map中不存在,那么就执行map.put(str,1),将字符串出现次数设置为1;如果str在map中存在,那么就执行map.put(str,map.get(str)+1),将字符串出现次数加1。遍历完成之后,可以很容易找出出现次数最多的100个字符串。字符串出现次数统计逻辑如图1-1所示。
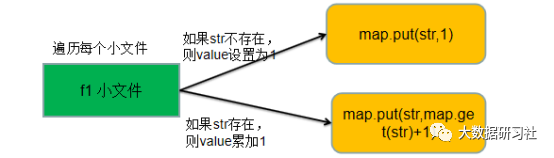
图1-1字符串出现次数统计逻辑
步骤3
基于第2步我们求解出了每个文件中出现次数最多的100个字符串,接下来只需要遍历第2步的统计结果,使用一个变量就可以找出重复次数最多的字符串。
方法总结:
在内存限定的情况下,求解海量数据的TopN或者Top1问题,都可以使用分治法进行解决。
题目描述:
有10个文件,每个文件1GB,每个文件的每一行存放的都是用户的query,每个文件的query都可能重复,现在要求按照query的频度排序。
题目解析:
针对本题目要考虑两种情况:
第1种情况:给定的内存足够大或者文件中的query重复度比较高,可以一次性把所有文件的query加载到内存中进行处理。
第2种情况:给定的内存不够或者文件中的query重复度不高,可用的内存无法存放所有文件中的query,那么就需要使用分治法来解决。
实现方式1:HashMap法
针对第1种情况,文件中的query重复度比较高,表明query的种类比较少,而且内存足够大,所以可以考虑把文件中所有的query都加载到内存中进行处理。
步骤1
首先遍历所有文件中的query,如果query存在与map中,则value值累加1;如果query不在map中,则value值设置为1。query出现次数统计逻辑如图1-1所示。
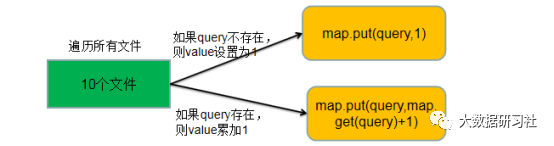
如图1-1 query出现次数统计逻辑
步骤2
基于第1步统计完所有query出现的次数之后,接下来可以对HashMap按照query出现的次数进行排序即可完成题目要求。
实现方式2:分治法
针对第2种情况,文件中query重复度不高,而且内存无法存储所有query数据,所以需要利用分治法来解决问题。
步骤1
首先需要根据数据量的大小和现有内存的大小,来确定问题划分的规模。目前就本题目来说,假定给定的内存为500M,可以遍历这10个文件中的query,通过Hash函数hash(query)%100将这些query划分到100个文件中,通过这样的划分,每个文件的大小约为100M,完全可以加载到500M的内存中进行处理。如果划分后的部分文件大小仍然超过500M,则采用同样的方式继续进行分解,直到划分后的每个小文件的大小都小于500M为止。文件分割过程如图1-1所示。
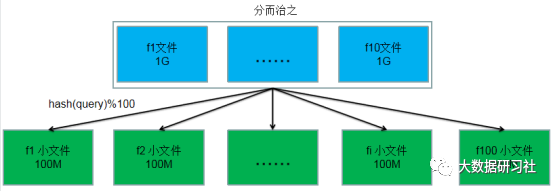
图1-1 文件分割过程
步骤2
然后统计每个query出现的次数,最简单的实现方式是使用HashMap来实现,其中key为query,value为该query出现的次数。具体做法是:针对每个小文件,遍历文件中的query,对于遍历到的query,如果query在map中不存在,那么就执行map.put(query,1),将query出现次数设置为1;如果query在map中存在,那么就执行map.put(query,map.get(query)+1),将query出现次数加1。接着按照query出现的次数value值排序,并将排序好的query以及value值输出到另外一个单独的文件中。那么针对每个输出文件,都是按照query的出现次数进行排序的。query出现次数统计逻辑如图1-1所示。
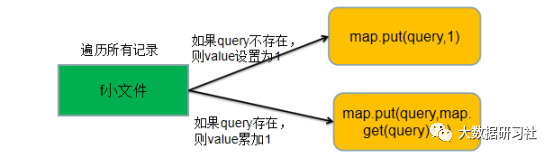
图1-1 query出现次数统计逻辑
步骤3
最后使用归并排序,对所有输出文件按照query的出现次数进行排序,就可以得到所有数据都是按照query的频度进行排序的结果。
题目描述:
给定a、b两个文件,各存放50亿个url,每个url各占64字节,内存限制为4G,现要求找出a、b两个文件中共同的url。
题目解析:
由于内存大小限制为4G,而每个URL占64字节,那么50亿个URL占用的空间大小约为50亿*64B≈320GB,因此我们无法一次性将所有URL加载到内存中进行处理,所以我们首先想到的是利用分治法来解决问题。
实现方式:分治法
步骤1
首先遍历a文件,对文件中遍历到的每个URL执行n=hash(URL)%1000操作,根据计算结果n将遍历到的URL映射存储到a0,a1,a2,a3,...,a999文件中,那么分割后的每个文件大小约为300M。a文件分割过程如图1-1所示。
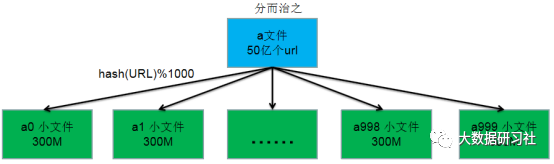
图1-1 a文件分割过程
步骤2
然后使用同样的方法遍历b文件,将b文件中的URL映射存储到b0,b1,b2,b3,...,b999文件中。这样处理完成之后,与ai文件中URL相同的URL一定在bi文件中,它们的对应关系为:a0对应b0,a1对应b1,a2对应b2,...,a999对应b999,ai和bi不对应的小文件不可能有相同的URL,因为它们使用的Hash函数是一样的。那么后续我们只需要统计出a和b对应的1000个小文件中相同的URL就可以了。b文件分割过程如图1-1所示。
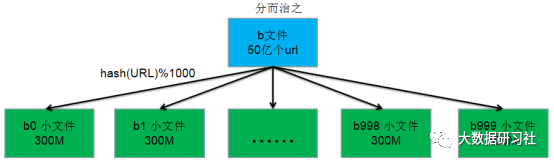
图1-1 b文件分割过程
步骤3
最后遍历ai文件,将遍历到的URL存储到一个HashSet集合中,接着遍历bi文件中的URL,如果这个URL在HashSet中存在,那么就说明这就是ai和bi文件共同的URL,可以把这个URL保存到一个单独的文件中。当遍历完从a0~a999的所有文件后,a和b两个文件中所有共同的URL都找到了。
题目描述:
从5亿个数中找出中位数。数据排序后,位置在最中间的数就是中位数。当样本数为奇数时,中位数为第(N+1)/2个数。当样本数为偶数时,中位数为第N/2个数与第 1+N/2个数的均值。
题目解析:
本题目中,有5亿个数字,每个数字在内存中占4个字节,那么5亿个数字需要的内存空间为5亿*4B=2GB内存。如果现有内存不足以加载所有数字,则可以采用分治法来解决问题。反之,我们可以采用双堆法。
实现方式1:分治法
步骤1
首先遍历这5亿个数字,针对读取到的数字digit,可以将其转换为二进制,二进制最高位为符号位,0表示为正,1表示为负。如果它对应的二进制中最高位为1,那么就把这个digit输出到fmin文件中,如果最高位为0,那么digit就输出到fmax文件中。经过这一步的处理,5亿个数字被分割为两个部分,并且fmax中的数字都大于fmin中的数字。文件分割过程如图1-1所示。
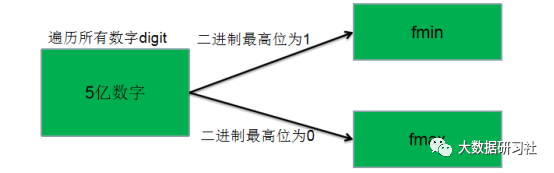
图1-1 文件分割过程
步骤2
经过第1步的处理之后,假设fmin中有1亿个数字,那么中位数一定在fmax文件中,而且为fmax文件中的第1.5亿个数开始的连续两个数求得的平均值。
步骤3
针对fmax文件可以使用同样的思路,使用二进制的次高位继续将fmax划分为两个文件。从而确定中位数是哪个文件的第几个数。类似的操作可以迭代进行,直到划分后的文件可以完全加载到内存中为止。
步骤4
经过上述操作之后,找到中位数所在的文件,并将该文件中的数据加载到内存中使用List集合进行排序,很容易找出中位数。还有一种特殊情况需要注意,当数字总数为偶数时,如果分割后的两个文件fmin和fmx的数字总数相同,那么中位数为fmin文件中的最大值与fmax文件中的最小值的平均值。
实现方式2:双堆法
当给定的内存可以完全加载5亿个数字时,我们可以选择双堆法来解决问题。这种方法的思路就是维护两个堆,一个大顶堆,一个小顶堆,而且这两个堆需要满足两个条件:
1.大顶堆中最大的数字小于等于小顶堆中最小的数字。
2.保证这两个堆中的数字个数的差值不能超过1。
当数字总数为偶数时,中位数就是两个堆顶元素的平均值。当数字总数为奇数的时,比较两个堆的大小,中位数就是数字总数最多的堆的堆顶元素。
步骤1
首先遍历5亿个数字,维护两个堆max-Heap(大顶堆)和min-Heap(小顶堆),其堆大小分别为maxSize和minSize,针对遍历到的每个数字digit,如果digit<max-Heap的堆顶元素,那么只能将digit插入到max-Heap中,但为了满足第二个条件,还需要分情况进行处理。
(1)当maxSize<=minSize,表明max-Heap的元素个数小于min-Heap的元素个数,此时将digit插入到max-Heap中,并重构max-Heap大顶堆。
(2)当maxSize>minSize,为了满足第二个条件,此时需要将max-Heap堆顶的元素移动到min-Heap中,然后将digit插入到max-Heap中,最后还需要重构min-Heap小顶堆和max-Heap大顶堆。
步骤2
如果max-Heap堆顶元素<=digit<=min-Heap堆顶的元素,此时情况较为复杂,我们需要分情况进行处理。
(1)当maxSize<minSize,就将digit插入到max-Heap中。
(2)当maxSize>minSize,就将digit插入到min-Heap中。
(3)当maxSize==minSize,将digit插入任意堆中都行。
步骤3
如果digit>min-Heap堆顶元素,那么只能将digit插入到min-Heap中,但为了满足第二个条件,还需要分情况进行处理。
(1)当maxSize>=minSize,就将digit插入到min-Heap。
(2)当maxSize<minSize,首先需要将min-Heap的堆顶元素移到max-Heap中,然后再将digit插入到min-Heap中。
步骤4
经过上述步骤处理,遍历完5亿个数字之后,就构造好了一个大顶堆(max-Heap)和一个小顶堆(min-Heap)。如果数据总数为奇数,就比较两个堆的大小,中位数就是数据量多的堆的堆顶元素。如果数据总数为偶数,那么中位数就是两个堆顶元素的平均值。双堆构造示意图如图1-1所示。
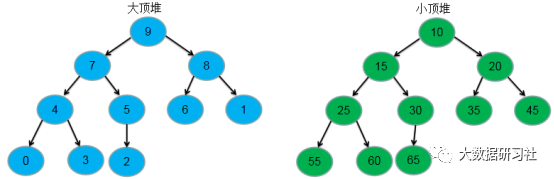
图1-1 双堆构造示意图
方法总结:
如果内存不足以容纳所有数据,则选择分治法。如果所有数据可以加载到内存中处理,则可以选择双堆法。
由于百度网盘链接经常被和谐,可以扫描下方微信二维码,备注【大数据算法面试】,然后通过网盘添加好友分享。

扫描上方微信二维码,添加好友,备注【大数据算法面试】,免费获取大数据算法面试文档。
完







