电力市场一个两阶段MPEC模型的构建和求解（二）

搬山道人的能源研究 2021-12-27

822

本文目的：求解上一期所构建的模型，得到发电商在两个市场的均衡策略，在文献或相关资料中，通过代码来实现所构建的模型大多没有细节部分，本文通过笔者的实践，尽量描述清楚这一过程的细节。

注：本文会使用gurobi求解器，gurobi基本的建模方式本文不在陈述，具体可参考Python|Gurobi——零基础学优化建模-NLP Python|Gurobi——零基础学优化建模，另外本文的代码通过python语言编写。

一、合约市场的代码实现

按照之前的分析，合约市场的算法逻辑如下图

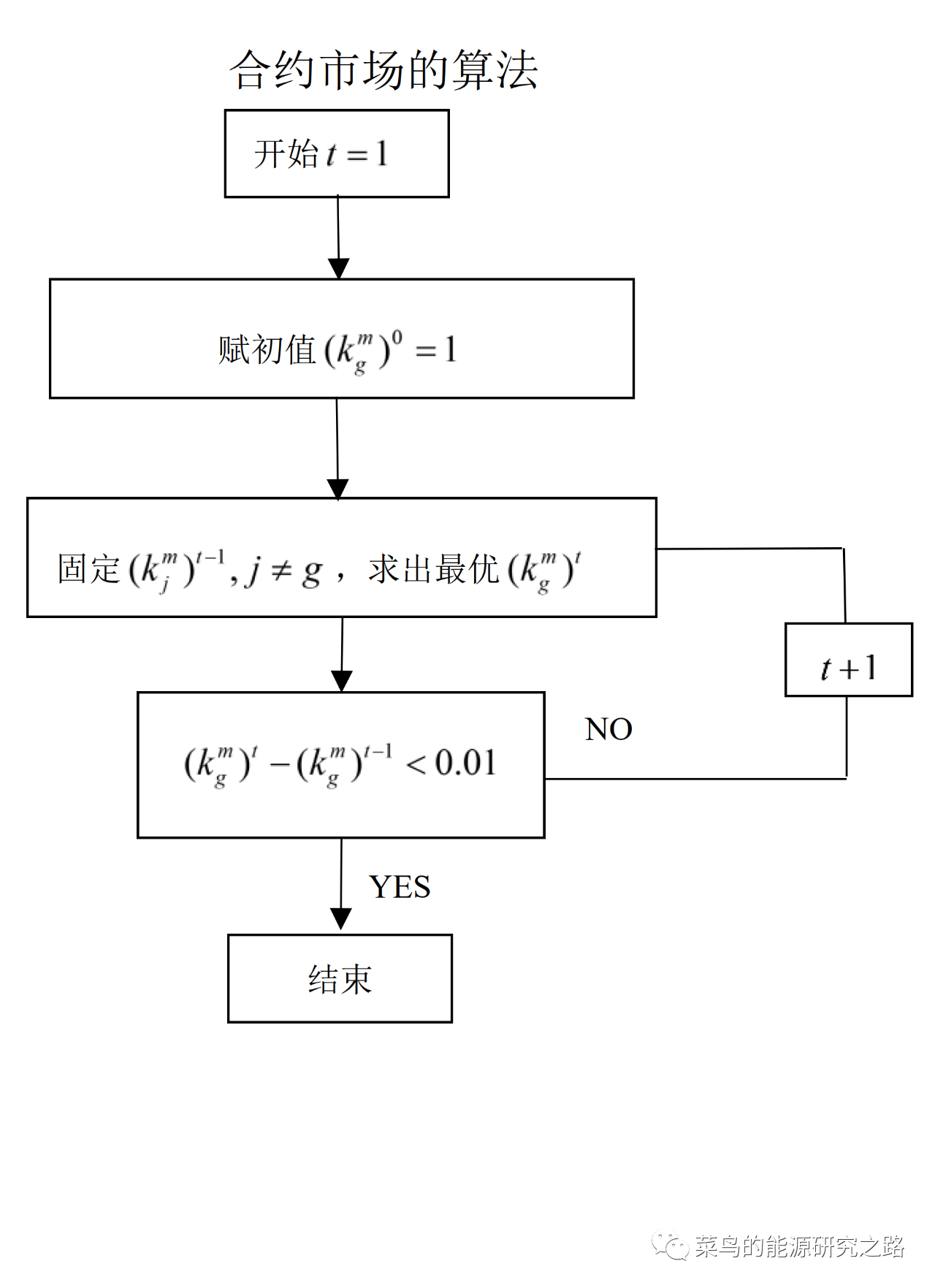
从上图分析可知，对于某一个发电商，是在固定其对手的策略下，求解其最优的策略，因此对每一个发电商来讲都为一个小的优化问题，这可通过Gurobi建模求解。进一步，迭代的每一轮中，每一个发电商最优问题的求解都可以在上一轮已经求解出的最优策略的基础上进行，直到迭代满足收敛的标准，即最终迭代出的最优策略会稳定在某一水平，偏差较小。

那么可以为每个发电商的优化模型定义为一个包含优化模型的函数，然后在主程序中不断的调用这个函数，直到迭代满足收敛要求。比如发电商1的优化模型如下：

import gurobipy as gp
from gurobipy import GRB


g_number = 5 #发电商的数量
a_gen = [30, 20, 30, 40, 40] #发电商的成本参数
b_gen = [0.03, 0.02, 0.03, 0.04, 0.15] #发电商的成本参数
A = 20000 #需求函数的参数A
B = 0.01  #需求函数的参数B
#发电商1的gurobi优化模型
def gen1(kgm2,kgm3,kgm4,kgm5,Eqg, Ep_spot):  #kgm2等为其余发电商的策略参数，
# Eqg为预期的发电商日前市场出清电量，为一个list ,包含5个发电商的数据，Ep_spot为日前市场出清的平均电价。
    
    model = gp.Model('foward')
    model.params.NonConvex = 2  # 模型为非线性规划模型，参数设置为2，具体见gurobi参考手册
    kgm1 = model.addVar(lb=1,ub=5,vtype=GRB.CONTINUOUS, name="kgm1")
    r = model.addVar(vtype=GRB.CONTINUOUS, name="r") #出清的合约电价
    qgc1 = model.addVar(vtype=GRB.CONTINUOUS, name="qgc1") #发电商1出清的合约电量
    z = model.addVar(vtype=GRB.CONTINUOUS, name="z") #定义额辅助变量
    y = model.addVar(vtype=GRB.CONTINUOUS, name="y") #定义的辅助变量
    
    con_z = model.addConstr(z == (1/(kgm1*b_gen[0])+1/(kgm2*b_gen[1])+1/(kgm3*b_gen[2])+1/(kgm4*b_gen[3])+1/(kgm5*b_gen[4])),name="con_z") #辅助变量约束
    con_y = model.addConstr(y == gp.quicksum(a_gen[number]/b_gen[number] for number in range(g_number)),name="con_y") #辅助变量约束
    con_price = model.addConstr(r*(B+z) == (A+y),name="con_price") # 均衡的合约价格约束
    con_qgc1 = model.addConstr(r == kgm1*(a_gen[0]+b_gen[0]*qgc1),name="con_qgc1")  #qgc1约束
    
    g1 = r*qgc1 + (Eqg[0]-qgc1)*Ep_spot - 0.5*b_gen[0]*qgc1*qgc1 - a_gen[0]*qgc1   #发电商1的目标函数
    var = model.getVars()
    kgm1 = var[0].x #提取计算的结果
    for v in Var:
            print(f"{v.varName}：{round(v.x,3)}")#打印变量的结果
    return kgm1 #返回发电商1的最优策略

其余发电商的优化模型代码同理可写，如下：

def gen2(kgm1,kgm3,kgm4,kgm5,Eqg, Ep_spot):  
.......
    return kgm2

def gen3(kgm1,kgm2,kgm4,kgm5,Eqg, Ep_spot):  
.......
    return kgm3

def gen4(kgm1,kgm2,kgm3,kgm5,Eqg, Ep_spot):  
.......
    return kgm4

def gen5(kgm1,kgm2,kgm3,kgm4,Eqg, Ep_spot):  
.......
    return kgm5

在写出5个发电商的优化模型函数之后，就开始写寻找合约市场均衡的代码，程序是不断通过迭代去收敛的，所以写一个for循环，代码如下：

for d in range(1,500):#发电商策略迭代都是在上一轮迭代的基础上进行的，同时赋所有发电商的初值为1
        kgm1[d] = forward_1.gen1(kgm2[d-1],kgm3[d-1],kgm4[d-1],kgm5[d-1],Eqg,Ep_spot)
        kgm2[d] = forward_1.gen2(kgm1[d-1],kgm3[d-1],kgm4[d-1],kgm5[d-1],Eqg,Ep_spot)
        kgm3[d] = forward_1.gen3(kgm1[d-1],kgm2[d-1],kgm4[d-1],kgm5[d-1],Eqg,Ep_spot)
        kgm4[d] = forward_1.gen4(kgm1[d-1],kgm2[d-1],kgm3[d-1],kgm5[d-1],Eqg,Ep_spot)
        kgm5[d] = forward_1.gen5(kgm1[d-1],kgm2[d-1],kgm3[d-1],kgm4[d-1],Eqg,Ep_spot)
        if abs(kgm1[d]-kgm1[d-1])<0.01 and abs(kgm2[d]-kgm2[d-1])<0.0.01 and abs(kgm3[d]-kgm3[d-1])<0.01 and abs(kgm4[d]-kgm4[d-1])<0.01 and abs(kgm5[d]-kgm5[d-1])<0.01:
            break #当满足迭代条件时跳出循环

注：代码中forward_1为模块名，因为笔者把所有发电商的函数都写在一个模块里面，所以在另外的主程序中需要使用模块名进行调用。运行程序后迭代几次就能找到均衡的策略。

二、日前市场的代码实现

日前市场的算法逻辑如下：

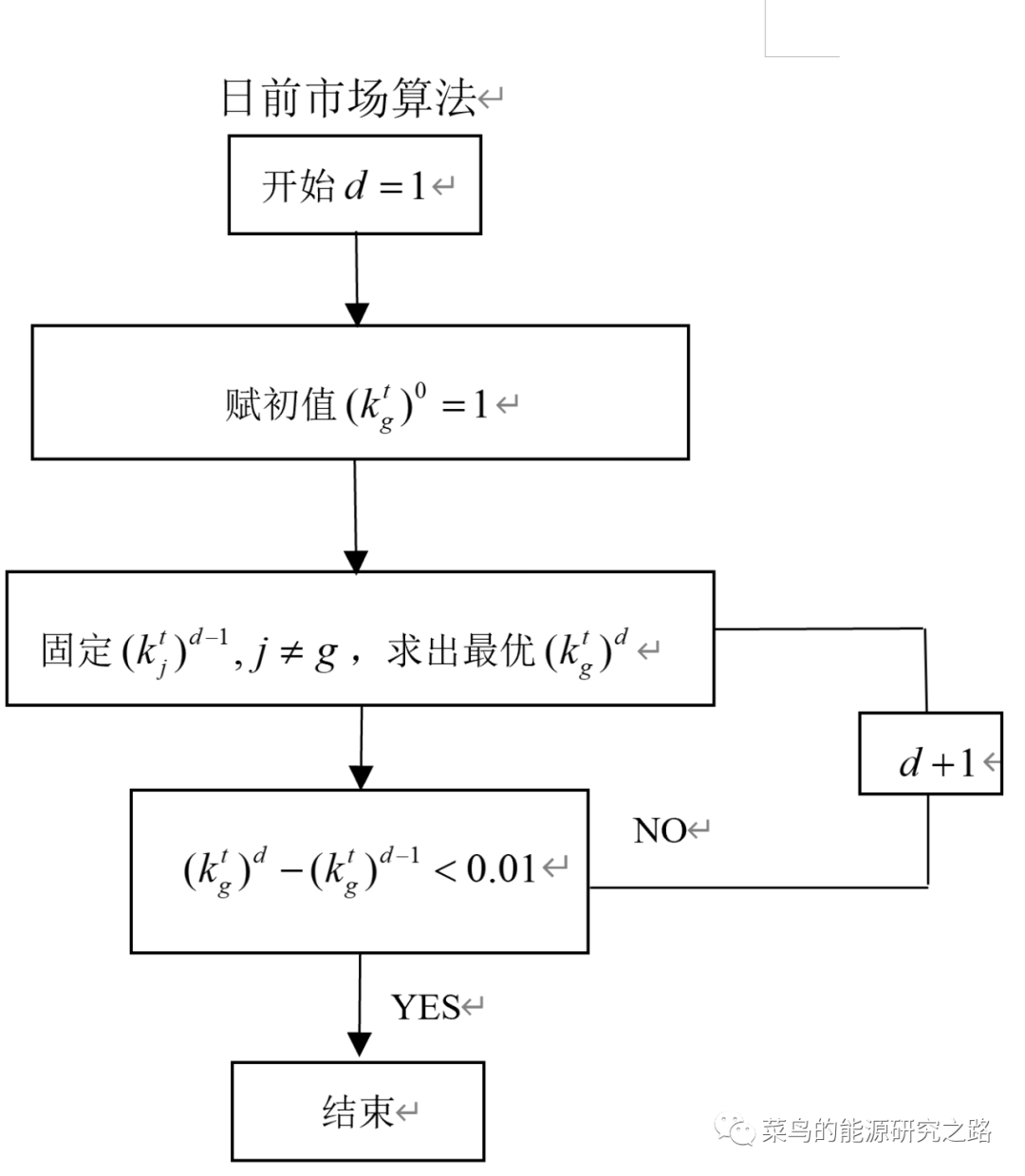
按照同样的思路，也可以为每个发电商的优化模型写一个函数，比如发电商1的优化模型代码如下：

import numpy as np
import gurobipy as gp
from gurobipy import GRB


n_period = [0.5, 0.3, 0.2]#在每个时段合约电量分配的比例
max_gen = [3800, 6000, 5000, 5500, 3000]#发电商的最大出力
M = 10000000 #松弛约束线性化处理后的设置的大M辅助变量


def gen1(kgt2,kgt3,kgt4,kgt5,r,qgc1,qm,demand_scene):
    result = [] #定义一个空列表，用于装计算的结果
    model = gp.Model('gen1')
    model.params.NonConvex = 2
    kgt1 = model.addVars(period, lb=1, ub=5,vtype=GRB.CONTINUOUS, name="kgt1")#发电商1的策略变量
    p_spot = model.addVars(period, lb=0, vtype=GRB.CONTINUOUS, name="p_spot")#日前市场的出清电价 
    qgt = model.addVars(g_number, period, lb=0,vtype=GRB.CONTINUOUS, name="qgt")#日前市场每个发电商的出清电量
    ugt = model.addVars(g_number, period, lb=0, vtype=GRB.CONTINUOUS,name="ugt")# 出力上限约束额朗格朗日乘子
    z = model.addVars(g_number, period,vtype=GRB.BINARY,name="z") 松弛约束线性化处理而设置的0,1变量
    #相应约束条件
    con_kgt1 = model.addConstrs(kgt1[j]*(a_gen[0]+b_gen[0]*qgt[0,j]) == p_spot[j] - ugt[0,j] for j in range(period))
    con_kgt2 = model.addConstrs(kgt2[j]*(a_gen[1]+b_gen[1]*qgt[1,j]) == p_spot[j] - ugt[1,j] for j in range(period))
    con_kgt3 = model.addConstrs(kgt3[j]*(a_gen[2]+b_gen[2]*qgt[2,j]) == p_spot[j] - ugt[2,j] for j in range(period))
    con_kgt4 = model.addConstrs(kgt4[j]*(a_gen[3]+b_gen[3]*qgt[3,j]) == p_spot[j] - ugt[3,j] for j in range(period))
    con_kgt5 = model.addConstrs(kgt5[j]*(a_gen[4]+b_gen[4]*qgt[4,j]) == p_spot[j] - ugt[4,j] for j in range(period))
    
    con_demand = model.addConstrs(qgt.sum('*',j) == n_period[j]*qm+demand_scene[j] for j in range(period))
    con_qgt_1 = model.addConstrs(qgt[i,j] <= max_gen[i] for i in range(g_number) for j in range(period))
    con_ugt = model.addConstrs(ugt[i,j] <= M*z[i,j] for i in range(g_number) for j in range(period))
    con_qgt_2 = model.addConstrs(max_gen[i] - qgt[i,j] <= M*(1-z[i,j]) for i in range(g_number) for j in range(period))
    
    #发电商1的目标函数
    g1 = (sum(p_spot[j]*qgt[0,j] + n_period[j]*qgc1*(r-p_spot[j]) for j in range(period)) - a_gen[0]*(qgt[0,0]+qgt[0,1]+qgt[0,2]) - 
                             0.5*b_gen[0]*(qgt[0,0]+qgt[0,1]+qgt[0,2])**2)


    model.setObjective(g1, GRB.MAXIMIZE)
    model.optimize()


    for v in model.getVars():  #打印出结果
        print(f"{v.varName}：{round(v.x,3)}")


    var = model.getVars()   #提取出清电量
    result.append(var[0].x)  
    result.append(var[1].x)
    result.append(var[2].x)


    return np.array(result)

注：（1）本程序对松弛约束进行了线性化处理，即上期模型（12）中的松弛约束变为：0<=Ugt<=M*Zgt和 0<=Max_q - qgt<=M*(1-Zgt)；（2）qm为总的合约市场的出清电量，由合约模型优化后每个发电商的出清电量加总即可；（3）demand_scene为上期模型（12）中的随机变量，在主程序中设置一定的分布自动生成。(4)模型最后返回一个np.array的结果是为了主程序好计算。

同理可写出每个发电商在日前市场的优化模型函数，同样通过for循环写出均衡结果的迭代程序。如下：

#赋初值
kgt1[0] = np.array([1,1,1])
kgt2[0] = np.array([1,1,1])
kgt3[0] = np.array([1,1,1])
kgt4[0] = np.array([1,1,1])
kgt5[0] = np.array([1,1,1])
e0 = np.array([0.01,0.01,0.01])
 
 for d in range(1,500):
        kgt1[d] = spot_1.gen1(kgt2[d-1],kgt3[d-1],kgt4[d-1],kgt5[d-1],r,qgc1,qm,demand_scene)
        kgt2[d] = spot_1.gen2(kgt1[d-1],kgt3[d-1],kgt4[d-1],kgt5[d-1],r,qgc2,qm,demand_scene)
        kgt3[d] = spot_1.gen3(kgt1[d-1],kgt2[d-1],kgt4[d-1],kgt5[d-1],r,qgc3,qm,demand_scene)
        kgt4[d] = spot_1.gen4(kgt1[d-1],kgt2[d-1],kgt3[d-1],kgt5[d-1],r,qgc4,qm,demand_scene)
        kgt5[d] = spot_1.gen5(kgt1[d-1],kgt2[d-1],kgt3[d-1],kgt4[d-1],r,qgc5,qm,demand_scene)
        if d % 2 == 0:
            e1[d] = abs(kgt1[d]-kgt1[d-2])
            e2[d] = abs(kgt2[d]-kgt2[d-2])
            e3[d] = abs(kgt3[d]-kgt3[d-2])
            e4[d] = abs(kgt4[d]-kgt4[d-2])
            e5[d] = abs(kgt5[d]-kgt5[d-2])
            if np.all(e1[d] < e0) and np.all(e2[d] < e0) and np.all(e3[d] < e0) and np.all(e4[d] < e0) and np.all(e5[d] < e0):
                break

注：（1）由于每个发电商的策略为三个时段的投标组成的，所以把初值设置为array结构；（2）从模型的运行结果来看，存在两个均衡，所以笔者取其给发电商最大利润的均衡，即选择了偶数轮的结果，当然也可以设置程序使得自身可以判断；（3）np.all函数为numpy库里的函数，含义为使得数列里每一个数都小于对应数列的数即可返回真；（4）模块spot_1同样为了书写日前市场的相关程序而设定的。

三、主程序实现两个市场的均衡

总的算法流程图如下：

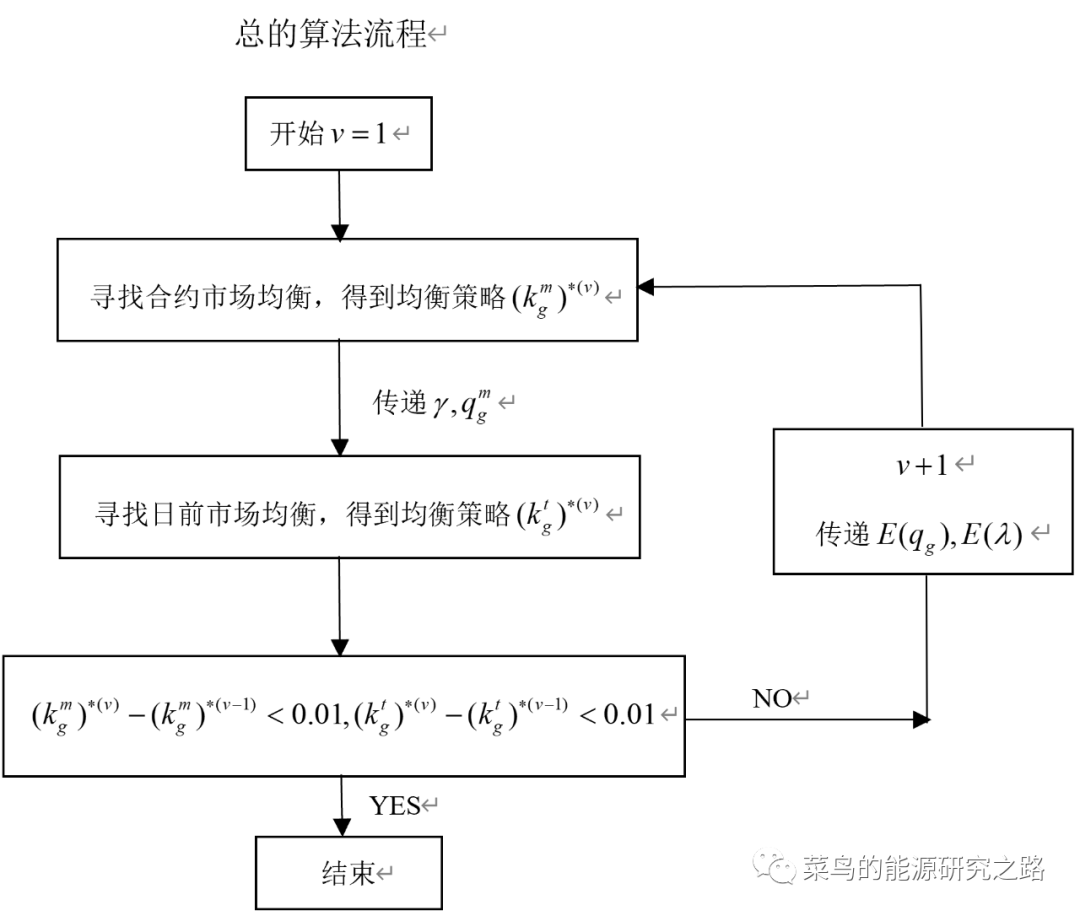
为方便主程序的书写，同样可以把寻找合约市场和日前市场的均衡封装在一个函数里面，便于调用，即定义forward_clean和spot_clean

  def forward_clean(Eqg,Ep_spot):  
      for d in range(1,500):
          kgm1[d] = forward_1.gen1(kgm2[d-1],kgm3[d-1],kgm4[d-1],kgm5[d-1],Eqg,Ep_spot)
          kgm2[d] = forward_1.gen2(kgm1[d-1],kgm3[d-1],kgm4[d-1],kgm5[d-1],Eqg,Ep_spot)
          kgm3[d] = forward_1.gen3(kgm1[d-1],kgm2[d-1],kgm4[d-1],kgm5[d-1],Eqg,Ep_spot)
          kgm4[d] = forward_1.gen4(kgm1[d-1],kgm2[d-1],kgm3[d-1],kgm5[d-1],Eqg,Ep_spot)
          kgm5[d] = forward_1.gen5(kgm1[d-1],kgm2[d-1],kgm3[d-1],kgm4[d-1],Eqg,Ep_spot)
          if abs(kgm1[d]-kgm1[d-1])<0.2 and abs(kgm2[d]-kgm2[d-1])<0.2 and abs(kgm3[d]-kgm3[d-1])<0.2 and abs(kgm4[d]-kgm4[d-1])<0.2 and abs(kgm5[d]-kgm5[d-1])<0.2:
            ............
              break
      return r,qgc1,qgc2,qgc3,qgc4,qgc5,qm

def spot_clean(r,qgc1,qgc2,qgc3,qgc4,qgc5,qm):
    for d in range(1,500):
        kgt1[d] = spot_1.gen1(kgt2[d-1],kgt3[d-1],kgt4[d-1],kgt5[d-1],r,qgc1,qm,demand_scene)
        kgt2[d] = spot_1.gen2(kgt1[d-1],kgt3[d-1],kgt4[d-1],kgt5[d-1],r,qgc2,qm,demand_scene)
        kgt3[d] = spot_1.gen3(kgt1[d-1],kgt2[d-1],kgt4[d-1],kgt5[d-1],r,qgc3,qm,demand_scene)
        kgt4[d] = spot_1.gen4(kgt1[d-1],kgt2[d-1],kgt3[d-1],kgt5[d-1],r,qgc4,qm,demand_scene)
        kgt5[d] = spot_1.gen5(kgt1[d-1],kgt2[d-1],kgt3[d-1],kgt4[d-1],r,qgc5,qm,demand_scene)
        if d % 2 == 0:
            e1[d] = abs(kgt1[d]-kgt1[d-2])
            e2[d] = abs(kgt2[d]-kgt2[d-2])
            e3[d] = abs(kgt3[d]-kgt3[d-2])
            e4[d] = abs(kgt4[d]-kgt4[d-2])
            e5[d] = abs(kgt5[d]-kgt5[d-2])
            if np.all(e1[d] < e0) and np.all(e2[d] < e0) and np.all(e3[d] < e0) and np.all(e4[d] < e0) and np.all(e5[d] < e0):
              .........
    return Eqg,Ep_spot #均衡的出清电量额电价的平均水平

注：省略号省略的是模型收敛后计算的相应的需要返回的结果，日前市场收敛后，得到的是每个发电商的均衡投标策略，因此可在pot_1中再写一个ISO的出清函数得到出清电价和每个发电商的出清电量，或者将均衡的策略随便带入某一个发电商的日前优化模型函数，本文采用的是另写一个ISO模型，即：

def ISO(kgt1,kgt2,kgt3,kgt4,kgt5,qm,demand_scene):
    result_q = {}
    p_spot={}
    model = gp.Model('ISO')
    model.params.NonConvex = 2
    qgt = model.addVars(g_number, period, vtype=GRB.CONTINUOUS, name="qgt")
    con_demand = model.addConstrs(qgt.sum('*',j) == n_period[j]*qm+demand_scene[j] for j in range(period))
    con_qgt = model.addConstrs(qgt[i,j] <= max_gen[i] for i in range(g_number) for j in range(period))
    #设置目标函数
    g1 = gp.quicksum(kgt1[j]*qgt[0,j]*(a_gen[0]+0.5*b_gen[0]*qgt[0,j]) for j in range(period))
    g2 = gp.quicksum(kgt2[j]*qgt[1,j]*(a_gen[1]+0.5*b_gen[1]*qgt[1,j]) for j in range(period))
    g3 = gp.quicksum(kgt3[j]*qgt[2,j]*(a_gen[2]+0.5*b_gen[2]*qgt[2,j]) for j in range(period))
    g4 = gp.quicksum(kgt4[j]*qgt[3,j]*(a_gen[3]+0.5*b_gen[3]*qgt[3,j]) for j in range(period))
    g5 = gp.quicksum(kgt5[j]*qgt[4,j]*(a_gen[4]+0.5*b_gen[4]*qgt[4,j]) for j in range(period))
    model.setObjective(g1+g2+g3+g4+g5, GRB.MINIMIZE)
    model.optimize()


    for v in model.getVars():  #打印出结果
        print(f"{v.varName}：{round(v.x,3)}")


    var = model.getVars()   #提取出清电量
    for v in range(15):
        i = v//3
        j = v%3
        result_q[i,j] = round(var[v].x,3)


    for i in range(5):  #计算出清电价
        if result_q[i,0] < max_gen[i] and result_q[i,1] < max_gen[i] and result_q[i,2] < max_gen[i]:
            for j in range(3):
                if i == 0:
                    p_spot[j] = kgt1[j]*(a_gen[0]+b_gen[0]*result_q[i,j])
                if i == 1:
                    p_spot[j] = kgt2[j]*(a_gen[1]+b_gen[1]*result_q[i,j])
                if i == 2:
                    p_spot[j] = kgt3[j]*(a_gen[2]+b_gen[2]*result_q[i,j])
                if i == 3:
                    p_spot[j] = kgt4[j]*(a_gen[3]+b_gen[3]*result_q[i,j])
                if i == 4:
                    p_spot[j] = kgt5[j]*(a_gen[4]+b_gen[4]*result_q[i,j])
    return result_q, p_spot

另外，本文的demand_scene为一个随机变量，在主程序中，设置其三个时段的值都服从均匀分布，然后设置多少种场景，就运行多少次日前市场的出清模型spot_clean，最后计算出预期的Eqg,Ep_spot。

demand_scene1 = random.uniform(1000, 2000)
demand_scene2 = random.uniform(500, 1000)
demand_scene3 = random.uniform(-200,200)
demand_scene = [demand_scene1,demand_scene2,demand_scene3]

优化策略迭代计算迭代模型 qm

文章转载自搬山道人的能源研究，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。

电力市场一个两阶段MPEC模型的构建和求解（二）

评论