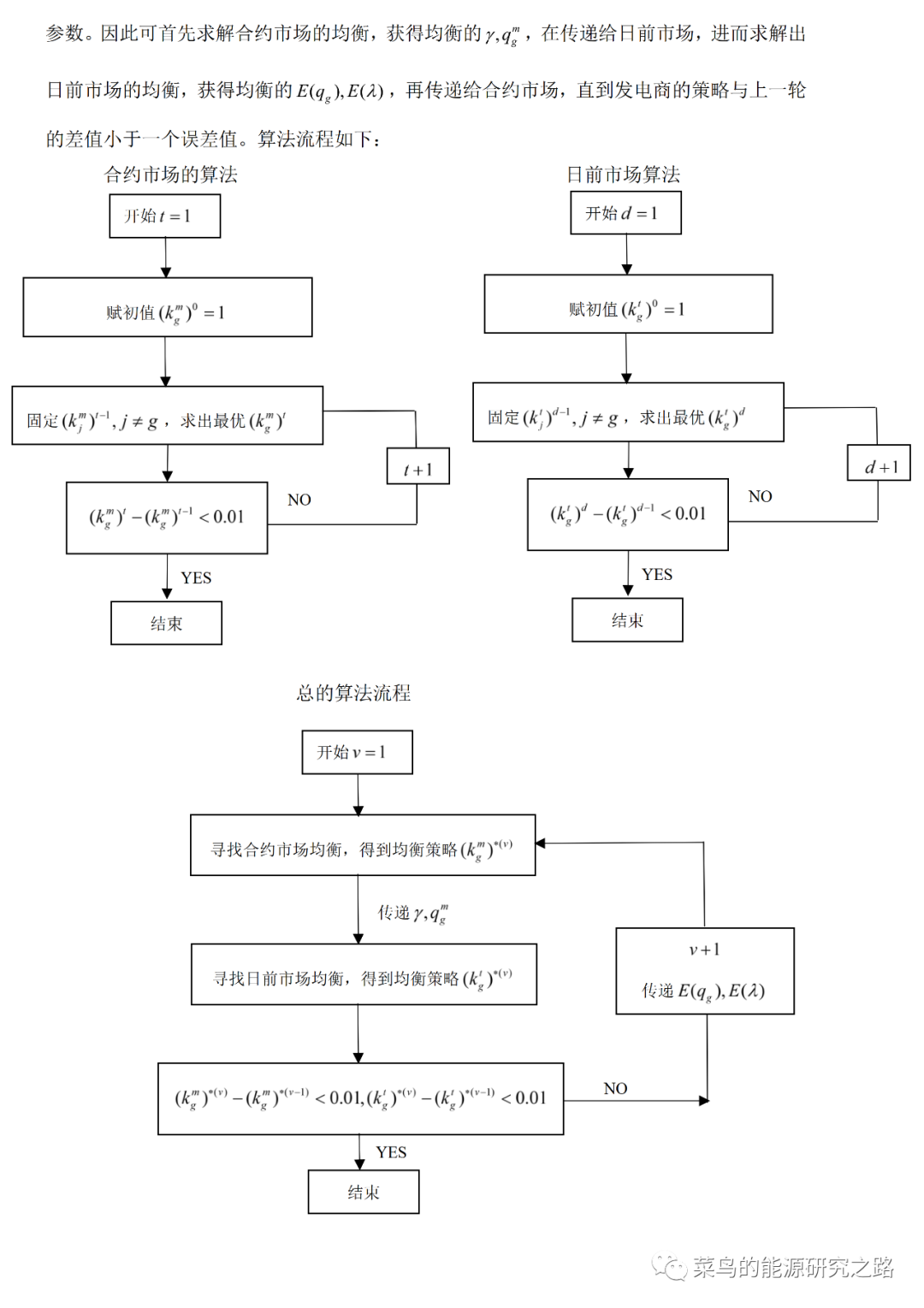
本文的目的:构建一个电力市场两阶段模型,利用商业求解器Gurobi和python语言对模型进行求解,得到电力市场的纳什均衡解,本期只描述模型的构建,模型的求解将在下一期进行。
本文的创新点:(1)MPEC模型在文献中有多种方法求解均衡,比如粒子群算法,协同进化,强化学习等,但这类智能算法都存在运行时间过长的缺点,本文试图直接通过成熟的商业求解器gurobi对模型进行求解,通过不断迭代去寻找发电商的最优策略,得到了较好的收敛效果;(2)本文所构建的模型是两阶段的,只有两个市场同时达到均衡才能得到最终的结果;(3)电力市场的实际需求通常是难以准确预测的,本文设置电力需求为一个随机变量,所以构建的模型为一个随机规划模型,在求解方式上,通过算法自身生成服从一定分布的数据。
一、模型背景
2015年电改“9”号文下发后,我国开启了新一轮的电力市场改革(简称“售电侧改革”),其旨在售电环节引入竞争,允许社会资本参与配售电业务,打破垄断售电格局,从而达到降低电价的目的。本次改革后,我国逐渐建立起了多层次的电力市场,并与国外成熟的电力市场接轨,具体讲,电力市场的架构如下:
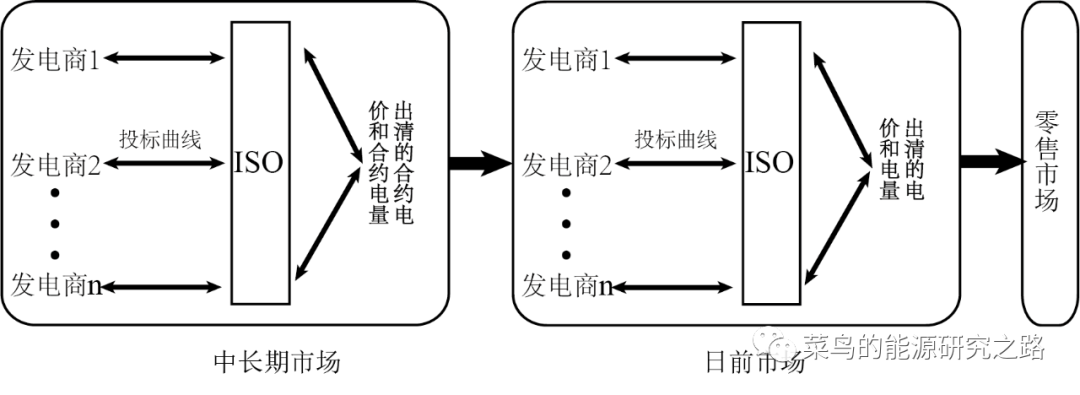
如图1所示,在售电环节中,我国大体上将建立中长期合约市场、现货市场(日前和实时市场)和零售市场(注:电力市场中还存在辅助市场、容量市场、输电权市场等,本文未考虑)。首先,发电商在中长期市场上签订电力合同,交易周、月、年或更长时间段的电量,可通过面对面(OTC)谈判的方式签订或者通过交易所的集中竞价方式签订,一般而言,参加交易所的方式更方便,成本也更低,所以大多市场参与者都会参与中长期合约的集中竞价。同时需要注意的是:建立在现货市场基础上的中长期市场,签订的合约是金融合约,且必须带分解曲线,而目前现行的中长期市场,签订的合约为物理合约,可不带曲线(注:我国的情况比较特殊,先构建了价差模式的中长期市场,然后在逐渐试点现货市场,今后的中长期市场将会与现行的中长期市场有很大的不同,具体可参考:我国电力市场直接交易竞价模式的经济学原理分析(五 广东2016年规则分析 );电力市场集中竞价的经济学原理分析 (十二 我国月度竞价市场中的偏差处理机制))。
在现货市场上(日前和实时市场),发电侧和负荷侧通过集中竞价的方式交易第一小时或一小时以内的电量,以此达到电量的平衡。现阶段,现货市场竞价规则采用“发电侧报价报量,负荷侧报量”的方式出清,即发电商向交易组织机构(ISO)提交报价曲线,报价随电量递增,表示提供一定数量的电量所需的最低价格(供给函数),而负荷侧只提交购电量,那么负荷侧将被动接受现货价格,是价格的接受者。ISO则以社会福利最大化(需求侧只提供报量时以发电商成本最低的出清原则)的原则进行出清,得到出清电价和每个发电商的出清电量。而中长期市场的集中竞价,参与双方都会报量报价。
电力实际需求通常是难以准确预测的,还加上机组临停检修等众多因素,现货市场的价格通常波动较大,为避免价格波动带来的风险,中长期市场统一签订差价合约形式的合同,其为一种金融合约,合同电量并不物理执行,只是在现货市场的出清结算中作为事后结算方式,具体结算规则为:签订的合约电量部分按合约价格结算,超出合约的电量按现货市场的统一市场清除价结算。根据这种结算方式,发电侧的总收入=上网电量×市场出清价+合约电量×(合约价格—现货电价),从结算方式上看,发电商可通过差价合约规避现货电价过低的风险。
综上分析,可以这样近似认为:发电侧和负荷侧在中长期市场和现货市场都会参与集中竞价,向交易所(ISO)提交曲线(实际中为分段曲线,本文近似为连续曲线),不同的是,负荷侧在中长期市场要提供曲线(需求曲线),而在现货市场上只提供量,即无弹性的曲线,交易所收集到参与者的报价数据后进行市场出清。所以在这两个市场上,参与者的策略变量为报价的参数。
二、模型构建
由于电力需求的弹性太小,所以可以假定市场需求曲线为固定的,(即:负荷侧的报价曲线固定),也就可以只考虑发电商的报价策略。那么,发电商的策略选择是建立在交易所出清结果的基础上,所以在两个市场中,发电商面临的都为一个双层模型,模型上层是发电商的目标函数(利润最大化),下层为ISO的出清模型(大多文献称为MPEC模型),下层模型可通过KKT条件进行转化,最终形成一个带均衡约束的非线性规划问题。