ICML  2022 | ProGCL: Rethinking Hard Negative Mining in Graph Contrastive Learning

“

文章信息

来源：Proceedings of the 39th International Conference on Machine Learning（ICML） 2022
标题：ProGCL: Rethinking Hard Negative Mining in Graph Contrastive Learning
作者：Jun Xia, Lirong Wu, Ge Wang, Jintao Chen, Stan Z. Li
链接：https://proceedings.mlr.press/v162/xia22b.html
代码：https://github.com/junxia97/ProGCL

”

内容简介

对比学习（CL）已成为无监督表示学习的主要技术，它将anchor的增强版本嵌入彼此靠近（正样本）并将其他样本（负样本）的嵌入分开。正如最近的研究所揭示的那样，CL 可以从hard example（与锚点最相似的底片）中受益。然而，当本文在图对比学习 (GCL) 中采用其他领域的现有hard negative挖掘技术时，本文观察到的好处有限。本文对这种现象进行了实验和理论分析，发现它可以归因于图神经网络（GNN）的消息传递。与其他领域的 CL 不同，如果仅根据锚点与自身的相似性来选择硬负样本，则大多数硬负样本都是潜在的假负样本（与锚点共享同一类的负样本），这将不希望地推开同一类的样本。为了弥补这一缺陷，本文提出了一种称为 ProGCL 的有效方法来估计负数为真的概率，这构成了更合适的负数硬度和相似性度量。此外，本文设计了两种方案（即 ProGCLweight 和 ProGCL-mix）来提高 GCL 的性能。大量实验表明，ProGCL 对基本 GCL 方法带来了显着且一致的改进，并在多个无监督基准上产生了多个最先进的结果，甚至超过了有监督基准的性能。此外，ProGCL 很容易插入到各种基于底片的 GCL 方法中以提高性能。

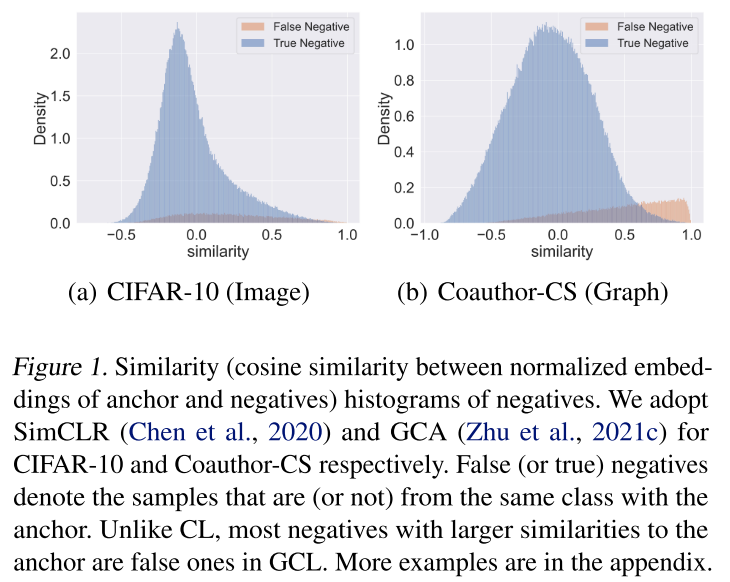当本文在 GCL 中采用负面挖掘技术时，本文观察到性能略有改善甚至显着下降（结果如下表所示）。为了解释这些现象，本文首先在下图中绘制了各种数据集相似性上的负数分布。请注意，在训练过程中，本文没有观察到负数分布的显着变化（如上图（a）所示保持单峰） SimCLR (Chen et al., 2020) 在 CIFAR-10 和其他图像数据集上。然而，对于 GCL 的第一阶段，底片的分布在很长一段时间内是双峰的，如上图（b），然后在第二阶段逐渐过渡到单峰分布，如 CL。更多数据集的类似现象可以在附录中找到。CL 和 GCL 之间负数分布的差异可以归因于图神经网络独特的消息传递，这些解释了 GCL 中现有的负挖掘技术性能不佳的原因。具体来说，他们将与锚点最相似的负数视为所有训练过程中的难点。然而，如上图(b) 所示，以这种方式选择的大多数“硬”负样本确实是 GCL 的假负样本，这将不希望地推开语义相似的样本，从而降低性能。假阴性的存在被称为 DCL 中的抽样偏差 (Chuang et al., 2020)。本文认为可以通过在相似性上拟合双分量（真-假）β 混合模型（BMM）来区分真假阴性。在 BMM 下，负数为真的后验概率可以构成更合适的测量负数硬度和相似性的方法。通过新的度量，本文设计了两种方案（ProGCL-weight 和 ProGCLmix）来进一步改进基于负数的 GCL 方法。据本文所知，本文的工作是在节点级 GCL 中研究硬负挖掘的开创性尝试之一。本文强调以下贡献：

• 本文展示了 GCL 和 CL 之间负数分布的差异，并通过理论和实验分析解释了为什么现有的硬负数挖掘技术在 GCL 中不能很好地工作。
• 本文建议利用BMM 来估计一个否定相对于特定锚为真的概率。结合相似性，本文得到了一个更合适的负片硬度度量。
• 本文设计了两种方案（即ProGCL-weight 和ProGCL-mix），它们更适合GCL 中的hardnegative 挖掘。
• ProGCL 对基本 GCL 方法带来了显着且一致的改进，并在多个无监督基准上产生了多个最先进的结果，甚至超过了有监督基准的性能。此外，它还可以增强各种基于底片的 GCL 方法以进一步改进。

方法介绍

实验和理论分析

在下图中，本文通过仅用 2 层 MLP 编码器替换由消息传递和多层感知器 (MLP) 组成的 2 层 GCN (Kipf & Welling, 2016a) 来研究消息传递在 GCL 中的作用。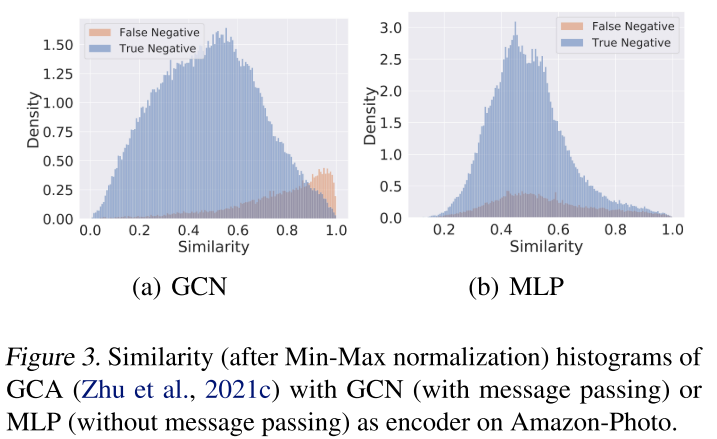可以观察到，GCL 的相似度直方图将与没有消息传递的 CL 相似，这验证了 GNN 编码器的消息传递是 CL 和 GCL 之间负数分布差异的关键因素。更具体地说，对于 GCL 的第一个双峰阶段，在 GCL 中传递的消息扩大了通常共享同一类的相邻节点之间的相似性。对于第二个单峰阶段，GCL 的实例判别占据了突出的位置，并推开了所有其他样本，而不管它们的语义类别如何。理论上，对于图 G 中任何节点对的嵌入，本文可以比较它们在消息传递之前和之后的距离，并表明距离将随着过程而减小。

ProGCL

本文的目标是估计否定的概率是真实的。从下图可以看出，GCL 中的假阴性和真阴性分布之间存在显着差异，可以从相似性分布中区分这两种类型的阴性。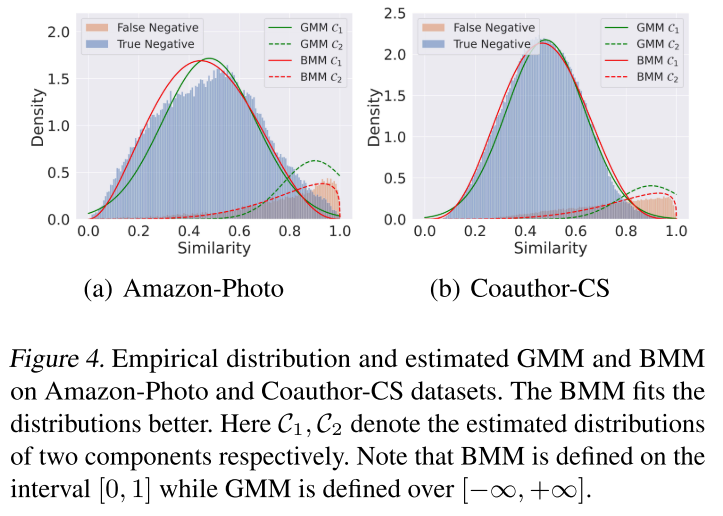在这里，本文建议利用混合模型来估计概率。高斯混合模型 (GMM) 是最流行的混合模型 (Lindsay, 1995)。然而，在上图中，假阴性的分布是倾斜的，因此对称高斯分布不能很好地拟合这一点。为了规避这个问题，本文求助于 beta 分布 (Gupta & Nadarajah, 2004; Ji et al., 2005)，它足够灵活，可以对 [0, 1] 上的各种分布（对称、偏斜、拱形分布等）进行建模。如上图所示，Beta 混合模型 (BMM) 可以比 GMM 更好地拟合经验分布。此外，本文在下表中比较了 ProGCL 与 BMM 和 GMM 的性能，发现 BMM 始终优于 GMM。贝塔分布的概率密度函数 (pdf) 是，

其中 是 beta 分布的参数， 是 gamma 函数。 上 分量的 beta 混合模型的 pdf（锚点和负数的归一化嵌入之间的最小-最大归一化余弦相似度）可以定义为：

方案一：ProGCL-权重

如上所述，GCL 存在严重的采样偏差，这将破坏性能。为了解决这个问题，本文提出了一种新的负片硬度测量方法，同时考虑了负片的硬度和概率为真:

其中是anchor 和它的采访负样本之间的相似度，表示相对于anchor 为真负的概率。注意 可用于对视图间 和视图内 负对进行加权，

然后本文可以将新的整体损失定义为所有正对的平均值，

方案二：ProGCL-mix

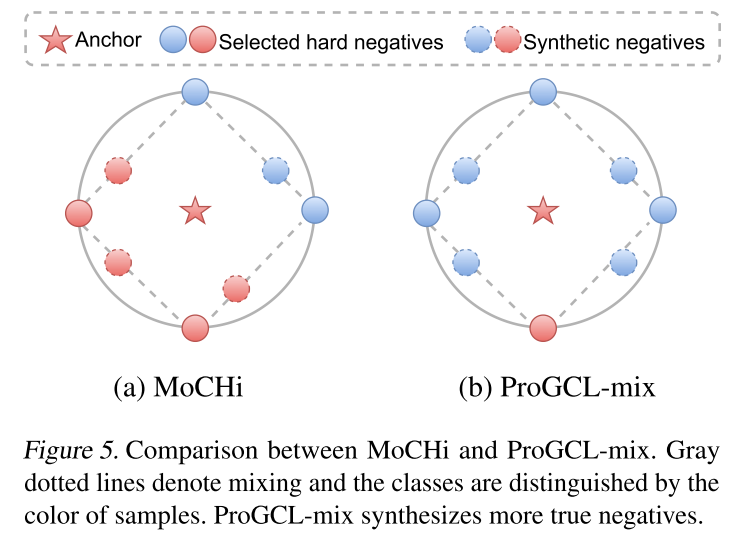
最近，MoCHi (Kalantidis et al., 2020) 提出使用仅通过相似性选择的“硬”负数来合成更多负数。然而，正如上面分析的那样，GCL 中许多合成的硬负样本确实是正样本，这会破坏性能。为了弥补这个缺陷，本文提出了 ProGCL-mix，它综合了更多的硬底片，考虑到负片是真实的概率。MoCHi 和 ProGCLmix 之间的比较可以在下图中看到。

更具体地说，对于每个锚点 ，本文通过其“最难”现有负数对的凸线性组合来合成 个硬负数。这里，“最难”的现有负数是指用等式中的度量选择的 个负数。本文不是随机混合 个样本，而是通过强调更可能为真阴性的样本来混合它们。形式上，对于每个锚 ，一个合成点 将由下式给出，

其中 和 是从测量的 “最难”的现有负数中选择的， 可以计算为:

然后，本文可以用合成的否定定义每个正对 的训练目标:

请注意，本文仅使用视图间硬底片合成新样本。最后，本文可以定义新的整体损失，

实验分析

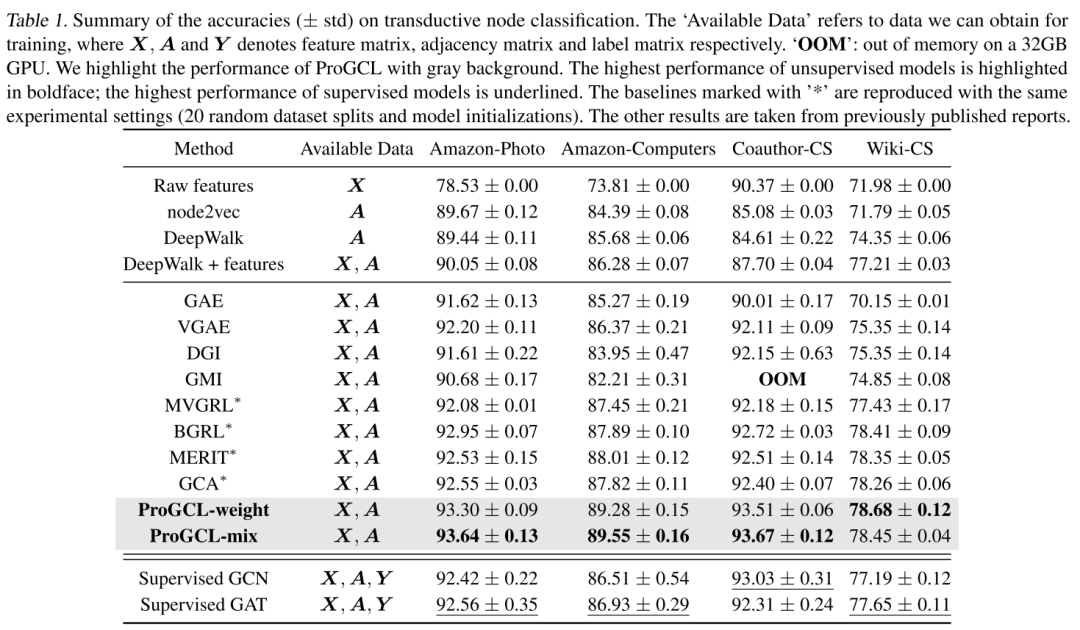
对于转导分类，如下表所示：

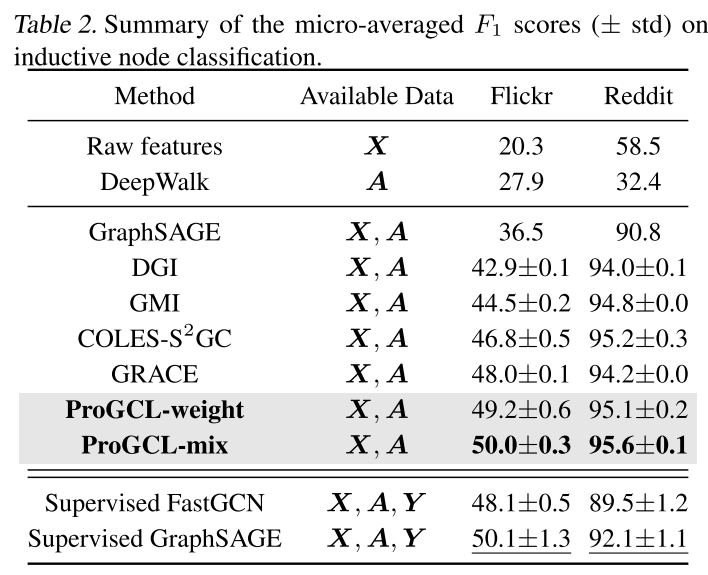
ProGCL 始终比以前的无监督基线甚至监督基线表现更好，这验证了本文的 ProGCL 的优越性。本文提供了更多的观察结果如下。首先，仅使用邻接矩阵的传统方法 node2vec 和 DeepWalk 优于仅使用亚马逊数据集上的原始特征（“原始特征”）的简单逻辑回归分类器。然而，后者在 Coauthor-CS 和 Wiki-CS 上表现更好。将两者结合起来（“DeepWalk + 功能”）可以带来显着的改进。与 GCA 相比，本文的 ProGCL 强调硬负样本或消除采样偏差，从而提高了表示质量。其次，ProGCL-mix 总体上比 ProGCL-weight 表现更好。对于归纳任务，ProGCL 还实现了优于其他基线的竞争性能，如下表所示。

总结

在本文中，本文解释了为什么现有的hard negative挖掘方法在 GCL 中不能很好地工作，并相反地引入 BMM 来估计否定为真的概率。此外，本文设计了两种方案来进一步提升GCL。未来工作的有趣方向包括（1）将 GCL 应用于更多现实世界的任务，包括社会分析和药物发现（Sun et al., 2021; Xia et al., 2022c）；(2)探索对比学习取得巨大成功的理论解释。