ICML  2022 | pathGCN: Learning General Graph Spatial Operators from Paths

“

文章信息

来源：Proceedings of the 39th International Conference on Machine Learning（ICML） 2022
标题：pathGCN: Learning General Graph Spatial Operators from Paths
作者：Moshe Eliasof, Eldad Haber, Eran Treister
链接：https://proceedings.mlr.press/v162/eliasof22a.html

”

内容简介

图卷积网络 (GCN) 与卷积神经网络 (CNN) 类似，通常基于两个主要操作——空间卷积和逐点卷积。在 GCN 的上下文中，与 CNN 不同，通常选择基于图拉普拉斯算子的预定空间算子，只允许学习逐点操作。然而，学习一个有意义的空间算子对于开发更具表现力的 GCN 以提高性能至关重要。本文提出了 pathGCN，这是一种从图上的随机路径中学习空间算子的新方法。作者分析了所提方法的收敛性及其与现有 GCN 的区别。此外，本文讨论了将学习的空间算子与逐点卷积相结合的几种选择。本文对大量数据集的广泛实验表明，通过正确学习空间卷积和逐点卷积，可以从本质上避免过度平滑等现象，并实现新的最先进的性能。

本文提出了 pathGCN——一种克服上述限制的新方法，基于图顶点上定义的随机路径的聚合。使用这种方法可以定义类似于图像二维卷积中使用的空间算子。这样的算子具有可变的孔径和系数，可以增加 GCN 的表现力。此外，由于算子的系数是学习的，它的特征值可能与图拉普拉斯算子的特征值有很大不同。这意味着学习的内核可以扮演不同的角色，从平滑到边缘检测（或锐化）算子。下图给出了由平滑空间核 [0.8, 1.0, 0.6] 诱导的有效空间算子的示例，其中可以看到空间算子同时依赖于图拓扑和空间核。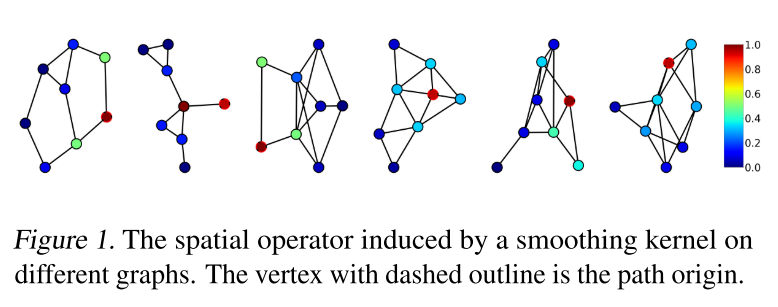

本文的主要贡献如下

• 本文介绍了 pathGCN——一种从随机路径学习 GCN 的表达性空间算子的新方法。pathGCN 支持多种公式，类似于标准 CNN——范围从全局到每层和每通道学习的空间运算符。
• 本文提供对pathGCN 行为的分析，并提出随机路径训练策略。
• 本文的实验通过在各种基准上获得和提高最先进的精度来揭示学习空间算子的重要性，同时还固有地防止过度平滑。

主要方法

学习空间算子

本文提出了对学习空间算子的需求。为此，首先考虑一个标准 CNN，其中数据位于一个简单的均匀网格上。注意到 CNN 和 GCN 都表示具有几何特征的数据。然而，虽然 CNN 是在简单的网格图上运行的网络，其中像素（节点）根据它们的位置链接，并且图的局部几何是固定的，但 GCN 可以被认为是局部几何变化的非结构化网格。

给定一个特征张量 ，CNN 中的卷积用 表示，是一个线性运算，其中每个输入通道和每个输出通道都有自己的空间算子。因此，每个线性算子 由张量 表示的 个不同的空间卷积组成。此外，卷积可以具有可变孔径（即内核大小），以获得更大的视野，并且通常是每层学习的，产生一组极具表现力的运算符。本文提出了一种方法，该方法允许在规则网格上构建类似于标准卷积的图卷积，这允许更大的表现力并且本质上不会过度平滑。

从固定到可变的空间算子

图的非恒定拓扑是在 GCN 中生成有意义的空间卷积的主要障碍。本文表明，这可以通过使用随机游走来解决。为此，考虑图上的一条路径，在该路径上学习参数化空间算子的权重。因此，需要一个在图上指示一些遍历策略的转换函数，以便获得类似于网络输入的路径。具体来说，本文采用来自 node2vec (Grover & Leskovec, 2016) 的图随机游走生成器，在 PyTorch-Geometric (Fey & Lenssen, 2019) 中实现，因为它的简单性和高效实现。

首先假设有一个单通道特征张量 ，并且给出了一条长度为 的路径。用 表示学习的空间参数，让 是长度为 的节点的单个随机路径的节点索引的元组，从节点 开始.第 个节点的单个路径上的卷积由以下线性算子定义：

即路径 %y_jsjp$ 个不同的路径，并相应地将路径卷积定义为所有采样路径的平均值:

其中 是从第 个节点开始的一组 个随机游走的路径。

构建路径pathGCN

本文定义了在空间域中运行的路径卷积。为了得到一个完整的网络，需要添加通道混合卷积和非线性激活，如下:

实验分析

本文展示了关于节点分类和蛋白质相互作用的 pathGCN (Hamilton et al., 2017)，然后进行了消融研究，以深入了解方法。在所有实验中，使用的网络由嵌入层（1×1 卷积）和一系列 pathGCN 层组成，其最终输出被馈送到充当分类器的 1×1 卷积层。在所有实验中使用 Adam (Kingma & Ba, 2014) 优化器，并对网络的超参数执行网格搜索。所有实验中的目标函数是交叉熵损失，除了在 PPI 上使用二元交叉熵损失的归纳学习。本文代码使用 PyTorch (Paszke et al., 2019) 和 PyTorch-Geometric (Fey & Lenssen, 2019) 实现，并在 Nvidia Titan RTX GPU 上进行了训练。

本文展示了所有考虑的任务和数据集，其统计数据在下表中提供。本文的方法要么更好，要么与其他最先进的模型相当。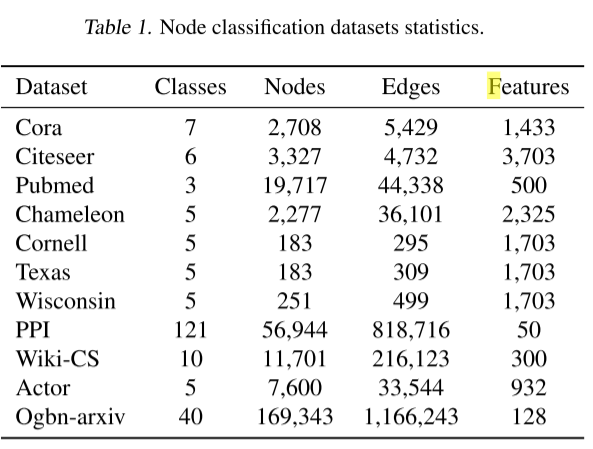

半监督节点分类

如下图所示，本文构建的 pathGCN 可以获得更宽的空间运算符，从而提高表达能力，即与基于图拉普拉斯算子或其代理的方法相比。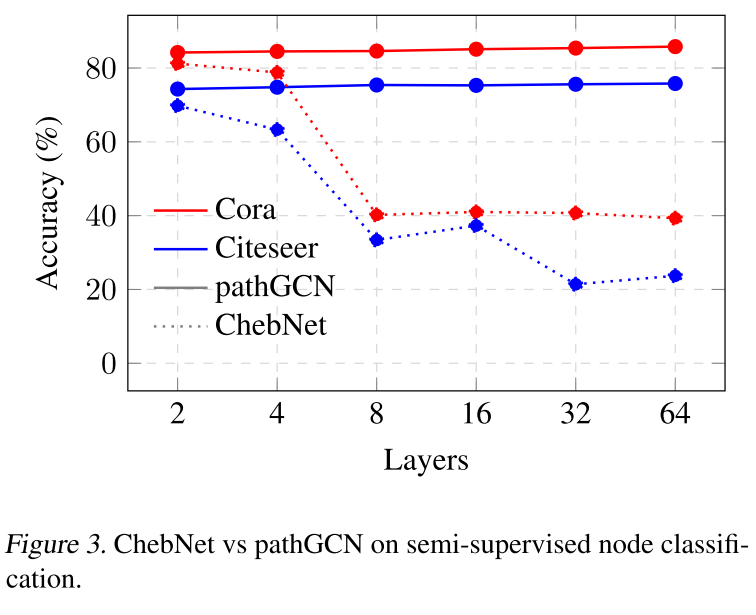

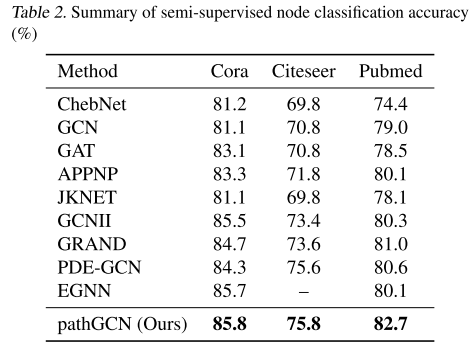
如下表所示，本文的 pathGCN 能够在所有三个数据集上获得更高的准确度。

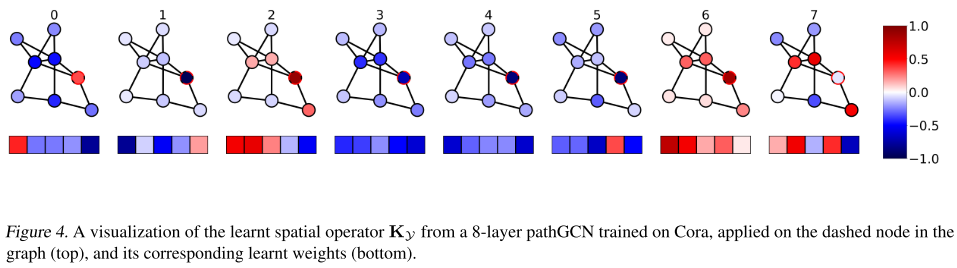
与之前最先进的 GRANDnl-rw 的 81.0% 相比，在 Pubmed 上获得了大胆的改进，准确率达到了 82.7%。本文的方法还受益于过度平滑的固有缺失，因为空间算子已完全学习。这也通过检查网络不同层的学习内核来验证。实际上，如下图所示，一些层通过平均来执行平滑，而另一些层则通过考虑沿路径的相邻节点的差异来充当边缘检测滤波器。

全监督节点分类

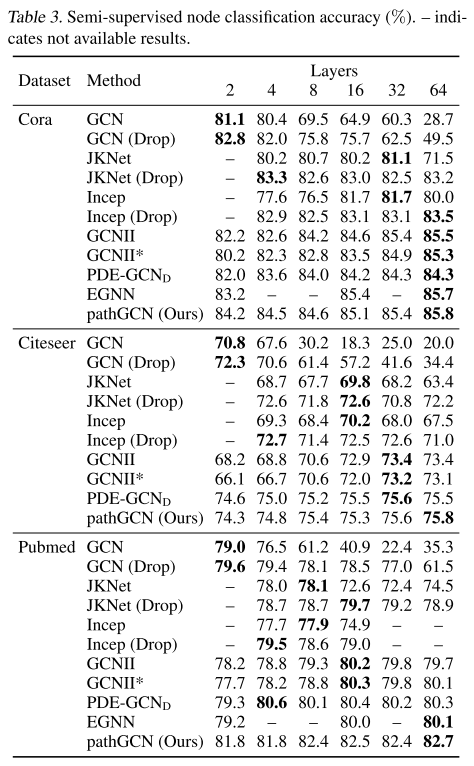
为了进一步验证方法，本文总共使用了 10 个数据集。本文还分别使用 60%、20%、20% 的相同训练/验证/测试拆分，并报告来自 (Pei et al., 2020) 的 10 个随机拆分的平均性能。将通道数固定为 64 并执行网格搜索以确定超参数。将本文的网络与表中的 GCN、GAT、Geom-GCN (Pei et al., 2020)、APPNP、JKNet、Inception、GCNII 和 PDE-GCN 进行了比较。

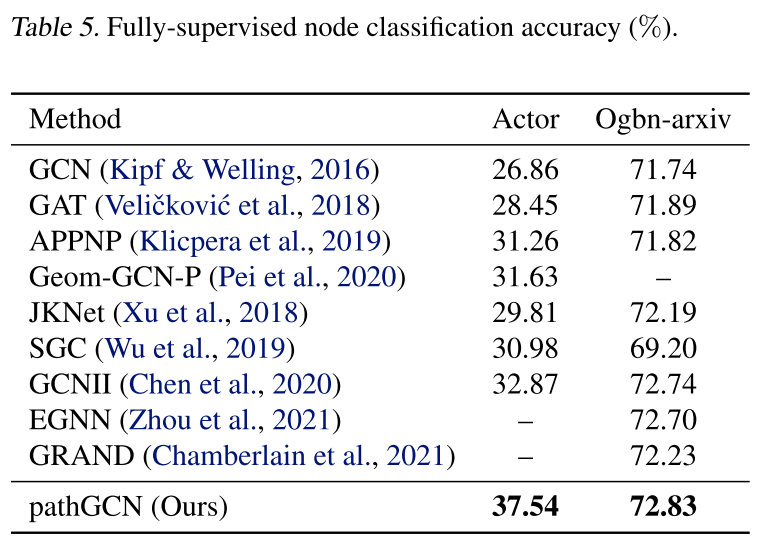
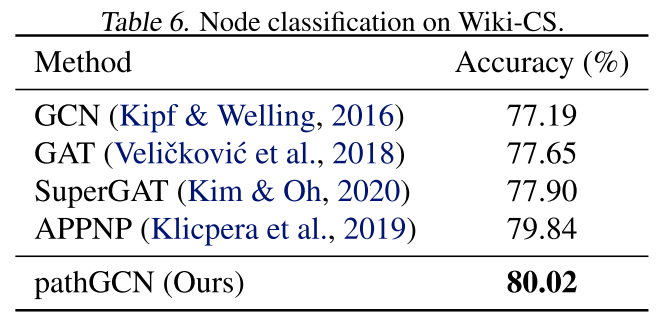
与所有考虑的方法相比，本文的实验获得了所有数据集的改进。例如，使用 pathGCN 在 Cora 上获得了 90.02% 的准确率，而 GCNII* 和 PDE-GCN 的准确率分别为 88.49% 和 88.60%。此外，使用 Actor (Pei et al., 2020)、Ogbnarxiv (Hu et al., 2020) 和 Wiki-CS (20 random splits) (Mernyei) 的标准训练/验证/测试拆分在更大的数据集上检查 pathGCN。在下表中可以再次看到所有考虑过的数据集的准确性提高。

总结

本文提出了一种学习 GCN 空间算子的新方法。作者的动机源于对具有表达空间内核的深度 GCN 的需求，类似于不会过度平滑的标准 CNN。本文的方法利用图上定义的路径来学习此类算子，进一步缩小 GCN 和 CNN 之间的差距。正如拉普拉斯算子不是用于 CNN 中图像的唯一空间算子一样，它在图和 GCN 的情况下也不一定是最佳的。为此，本文提出了 pathGCN，它用完全学习的内核代替了基于拉普拉斯算子的算子。事实上，实验表明，可以根据手头的数据和任务学习更具表现力的内核，从而在众多应用程序和数据集上始终保持更高的准确性，并且不会过度平滑。