ICML  2022 | The Infinite Contextual Graph Markov Model

文章信息

「来源」：Proceedings of the 39th International Conference on Machine Learning（ICML） 2022
「标题」：The Infinite Contextual Graph Markov Model
「作者」：Daniele Castellana, Federico Errica, Davide Bacciu, Alessio Micheli
「链接」：https://proceedings.mlr.press/v162/castellana22a.html
「代码」：https://github.com/diningphil/iCGMM

内容简介

上下文图马尔可夫模型 (CGMM) 是一种深度、无监督和概率模型，用于逐层递增训练的图。与大多数深度图网络一样，一个固有的限制是需要执行广泛的模型选择来选择每个层的潜在表示适当大小。本文通过引入无限上下文图马尔可夫模型（ICGMM）来解决这个问题，「这是第一个用于图学习的深度贝叶斯非参数模型。在训练过程中，ICGMM 可以调整每一层的复杂度，以更好地拟合底层数据分布」。在 8 个图分类任务中，本文展示了 ICGMM 成功恢复或提高了 CGMM 的性能，同时减少了超参数的搜索空间，且与大多数端到端监督方法的性能相当。结果包括关于深度、超参数和图嵌入压缩的重要性的研究。本文还介绍了一种新颖的近似推理程序，可以更好地处理更大的图拓扑。

CGMM 训练许多贝叶斯网络，其中每一层都以在前一层计算的图节点冻结后验为条件。每一层都使用期望最大化 (EM) 算法 (Moon, 1996) 和封闭式解决方案来优化数据的可能性。与其神经对应物一样，每层中隐藏单元的数量通常被选为超参数，「CGMM 依赖于模型选择来选择与分类潜在变量相关联的“合理”数量的隐藏状态。然而，与神经方法不同的是，CGMM 适合于 BNP 扩展，因为每一层本质上都是一个条件混合模型」。

出于这些原因，「本文的目标是设计一个用于图学习的深度贝叶斯非参数模型」，该模型可以从数据本身估计大多数超参数的值，例如状态数，通过提供 CGMM 的贝叶斯非参数处理来实现这一点。「主要困难在于如何处理每个节点的可变大小邻节点数」，在 CGMM 中，这通过邻居后验分布的（可能加权的）凸组合来解决。由此产生的模型，称为无限上下文图马尔可夫模型 (ICGMM)，可以根据需要生成尽可能多的潜在状态，以解决每一层的无监督密度估计任务。据作者研究，这是第一个用于自适应图处理的贝叶斯非参数模型。本文遵循公平、稳健和可重复的实验程序，在八种不同的图分类任务上比较了 ICGMM 与 CGMM 以及端到端监督方法。结果表明，「ICGMM 可以在不牺牲其预测性能的情况下推断其大部分超参数」。本文实验证明 ICGMM 的分数与 CGMM 相当或更好，并且这些分数可与最先进的监督方法相媲美。作者通过研究深度如何影响性能以及剩余超参数如何影响所选潜在状态的数量来补充分析。反过来，后者对最终无监督图嵌入的大小有显着影响。作为进一步的贡献，本文提供了一种更快的方法实现，该方法可以扩展到本工作中考虑的社会数据集，而没有任何性能变化。作者希望展示来自不同研究领域的想法的交叉融合如何帮助作者在方法论和经验意义上推进最先进的技术。

方案介绍

模型定义

本文将图定义为元组 其中 是实体集（也称为节点或顶点）， 是连接节点 u 到 v 的有向边 (u, v) 集, 符号 代表与图 g 相关的节点属性集。此外，节点 u 的邻域是连接到 u 的节点集，即 。为了这项工作的目的，我们将使用术语 定义节点 u 的（分类或连续）节点特征。

从架构上讲，ICGMM 与传统的 CGMM 具有相同的特征，而下图中突出显示了每一层的图形模型的差异。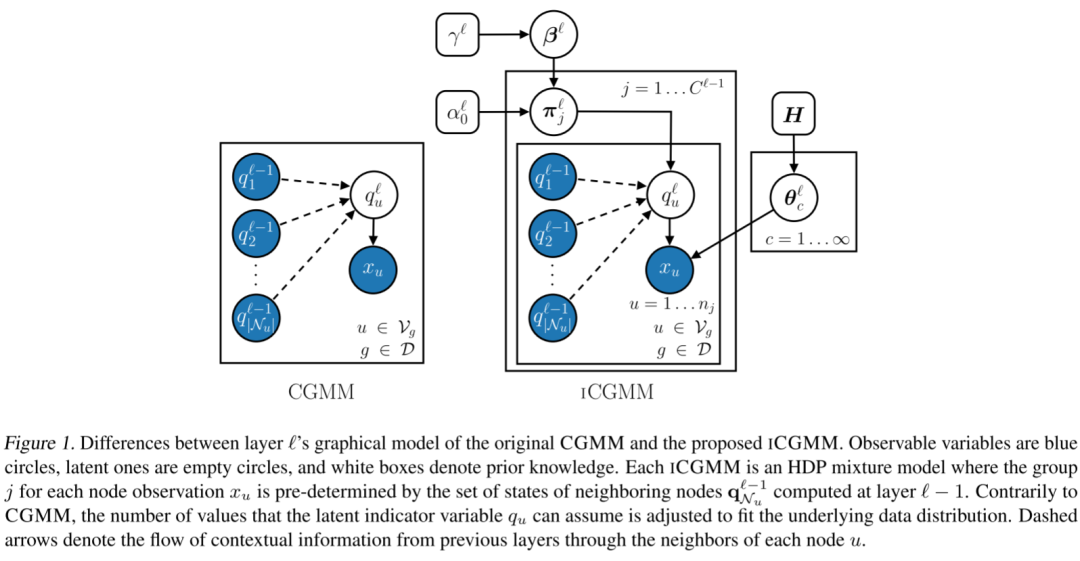特别是，ICGMM 假设每一层的节点特征 的生成由 HDP 控制混合模型。单个 ICGMM 层 的生成过程可以形式化如下：

作者将上标 ℓ 添加到 HDP 混合模型数量中，以突出它们在每个 ICGMM 层中是不同的。与 HDP 的情况类似，本文使用 来表示模型在当前层选择的状态数。当从上下文中清楚时，将省略这样的上标以简化符号。如前所述，在任何 HDP 混合模型中，每个观测值都必须属于一个组，并且该组通常是预先知道的。相反，在本文中，每个 ICGMM 层可以通过利用图中的结构信息为每个观察分配一个组。这样可以有效地让节点在彼此之间传播上下文信息。本文根据邻居的可观察后验 选择特征节点 的组 :

已被选为 大小的宏观状态中最有可能的位置，该位置是通过对 中的邻居概率进行平均而获得的。

图嵌入生成

与论文(Bacciu et al., 2020a)中所提方法类似，本文在最后一次迭代中使用样本分布。这样将有关状态占用的更多信息编码到节点/图嵌入中。如Bacciu 等人提出的每一层的节点嵌入都表示为unibigrams的方法。Unibigram 将节点的后部（即称为 unigram 的向量）与它的 bigram 连接起来。对于每个可能的状态 ，二元组计算 u 的邻居中有多少处于另一个状态，它表示为大小为 的向量。最终的图表示是通过在所有层上连接节点unibigrams，然后进行全局聚合来获得的。为了处理监督任务，本文在无监督节点/图嵌入之上应用“标准”预测器，例如多层感知器 (MLP)。

使用节点批次进行更快的推理

本文更喜欢通过引入近似而不是依赖于精确的分布式计算来加速推理过程。正如 Gal & Ghahramani (2014) 中所建议的，近似推理过程足以解决许多问题。本文的建议是对一批节点观察并行执行采样。通过这种方式，必要的统计数据可以批量更新，而不是单独更新，并且可以使用矩阵运算来提高效率。为了在质量和加速之间保持良好的平衡，本文坚持使用 1 个图作为批次的大小。这种权衡在训练时提供了高达 60 倍的 CPU 加速，作者凭经验观察到，在所考虑的较小化学任务上，性能相对于原始版本保持不变。虽然这个更快版本的 ICGMM（称之为 ICGMMf）并没有严格遵守上一节的技术规范，但作者认为优点在很大程度上优于缺点。有兴趣的读者可以参考附录 D 来分析不同数据集的加速增益。

实验分析

本文使用 Errica 等人定义的图分类的公平、稳健和可重复的评估设置来评估 ICGMM 的性能。它包括用于模型评估的外部 10 折交叉验证，然后是用于每个外部折叠的内部保留模型选择。已经提供了分层数据拆分；在这方面，作者通过尝试原始论文中指定的所有超参数（特别是尝试过的 分别为 5、10 和 20）。本文首先在三个化学数据集 D&D (Dobson & Doig, 2003)、NCI1 (Wale et al., 2008) 和 PROTEINS (Borgwardt et al., 2005) 上进行实验，其中节点特征代表原子类型。然后考虑社交数据集，包括 IMDB-BINARY、IMDB-MULTI、REDDIT-BINARY、REDDIT-MULTI-5K 和 COLLAB (Yanardag & Vishwanathan, 2015)，其中每个节点的度数是唯一可用的连续特征。所有数据集都是公开的（Kersting et al，2016 ），其统计数据总结在附录 C 中。最后，本文依靠 Pytorch Geometric（Fey & Lenssen，2019 ）来进行实验。

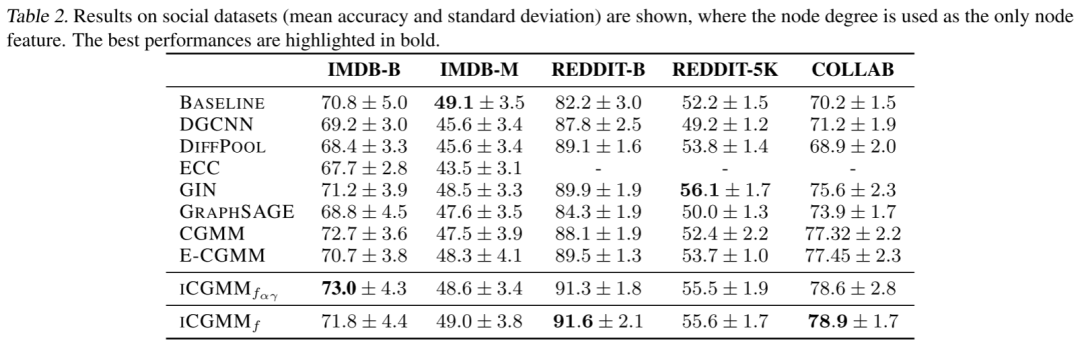
在化学和社交基准数据集上的实证结果分别在下表中报告。从化学任务开始，需要进行一些观察。首先，ICGMM 与 CGMM、E-CGMM 和大多数监督神经模型的性能相似；这表明基于相邻推荐的选择是图节点之间信息传播的一种微妙但有效的形式。此外，结果表明在不影响整体准确性的情况下有效地选择了潜在状态的数量，这是本文工作的主要目标。最后，ICGMMf 的性能与精确版本一样好，因此可以安全地将更快的变体应用于更大的社交数据集。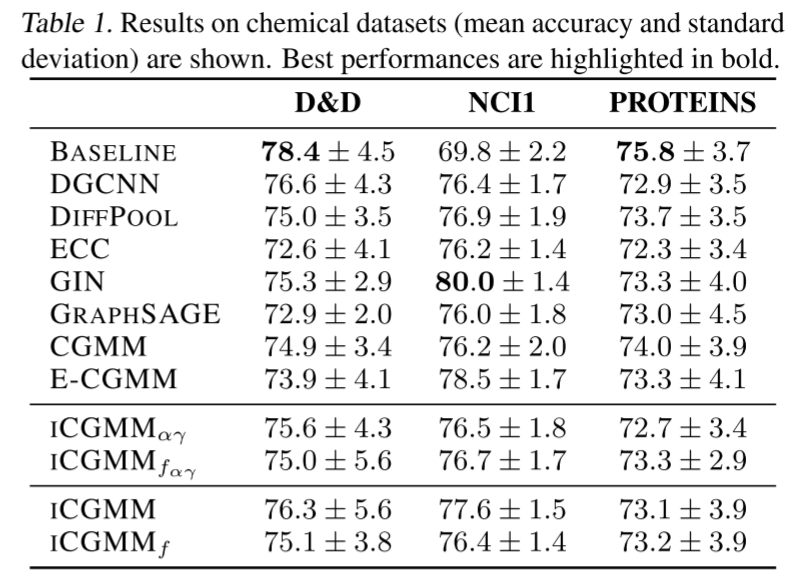

总结

通过无限上下文图马尔可夫模型，本文「弥合了贝叶斯非参数技术和图机器学习之间的差距」。本文已经描述了所提方法如何「推断每个无监督层的状态数量和大多数超参数，从而减少模型选择期间要尝试的配置数量」。正如实证分析表明的那样，该模型「不仅可以利用深度来提高其泛化性能，而且它还可以产生比 CGMM 更小的嵌入，从而节省内存占用和后续分类器的训练时间」。出于这些原因，作者认为 ICGMM 代表了在理论上构建图的完全概率深度学习模型的第一个相关步骤。