在日常生活中,我们经常会遇到一些问题,在字处理软件中,检查一个单词是否拼写正确(单词是否在已有的字典中);在FBI,犯罪嫌疑人的名字是否在嫌疑名单中;在网络爬虫里,一个网址是否已经被访问过;在垃圾邮件过滤中,判断一份垃圾邮件是否在垃圾邮件的名单中。
在传统的解决方案中,我们可以利用一些数据结构进行完成,比如:
数组:我们可以将该元素在数组中利用遍历的方式判断是否存在;
链表:我们可以将该元素在链表中利用遍历的方式判断是否存在;
树、平衡二叉树:我们可以将该元素在树中进行遍历,如果是平衡二叉树的话,效率相当于二分查找法;
哈希表:存储在哈希表中按键取值做比对的方式来判断是否存在。
但是一般来讲,当计算机运行的时候,都是在内存中去完成逻辑判断,在较小的数据量中,以上的判断方式是可以胜任的,当数据量大到了一定量级,比如500万条记录甚至1亿条记录的时候, 这时候常规数据结构的问题就凸显出来了,数组、链表和树的数据结果在大量级的数据面前,消耗的内存会呈现线性增长并最终达到瓶颈。哈希表的查询效率达到了O(1),但是哈希表在存储的时候是利用哈希函数进行映射的的,存储的效率通常小于50%(哈希冲突),一般来讲,如果一个email地址映射成8个字节的指纹信息,一亿条将消耗的内存是 8 * 2 * 1亿=1.6G(8个字节按50%的存储效率估计再乘以1亿条数据得出的预估结果),普通计算机和服务器是无法为满足此类的一次逻辑判断产生便如此巨大的内存开销的。
以上问题的本质其实概括起来讲就是,判断一个元素是否在超大集合中是否存在,既然传统的数据结构难以解决这个问题,那么布隆过滤器也就应运而生了。
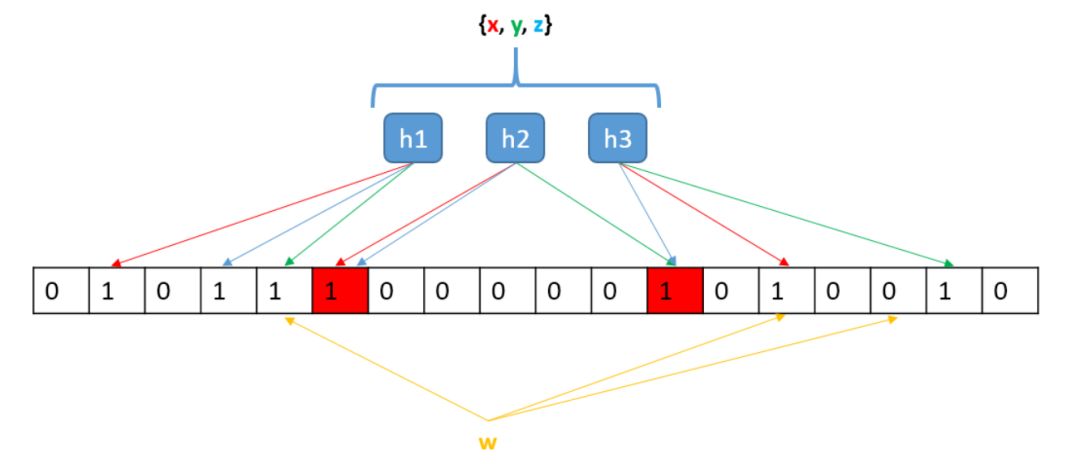
布隆过滤器实际上是由一个很长的二进制矢量和一系列的随机映射函数组成。其中【很长的二进制矢量】可以理解成一个很长的bit数组,采取bit数组的好处就是节省空间(1Byte=8bit,1KB=1024Byte),如果我们要存放一个100亿长度的bit数组会用到多少内存空间呢,答案是1.2G的内存空间,如果是100亿条8字节的指纹信息存放在HashMap中将会消耗160G的内存空间;【一系列随机函数】可以理解成有多个哈希函数。布隆过滤器优化查询性能的原理就是加速判断查找和判断是否存在,如果事先通过布隆过滤器判断该元素不在大集合中,则会减少之后所产生的磁盘读写和网络请求的消耗,节省后续昂贵的查询请求。下面举个例子来讲述下布隆过滤器的工作过程。
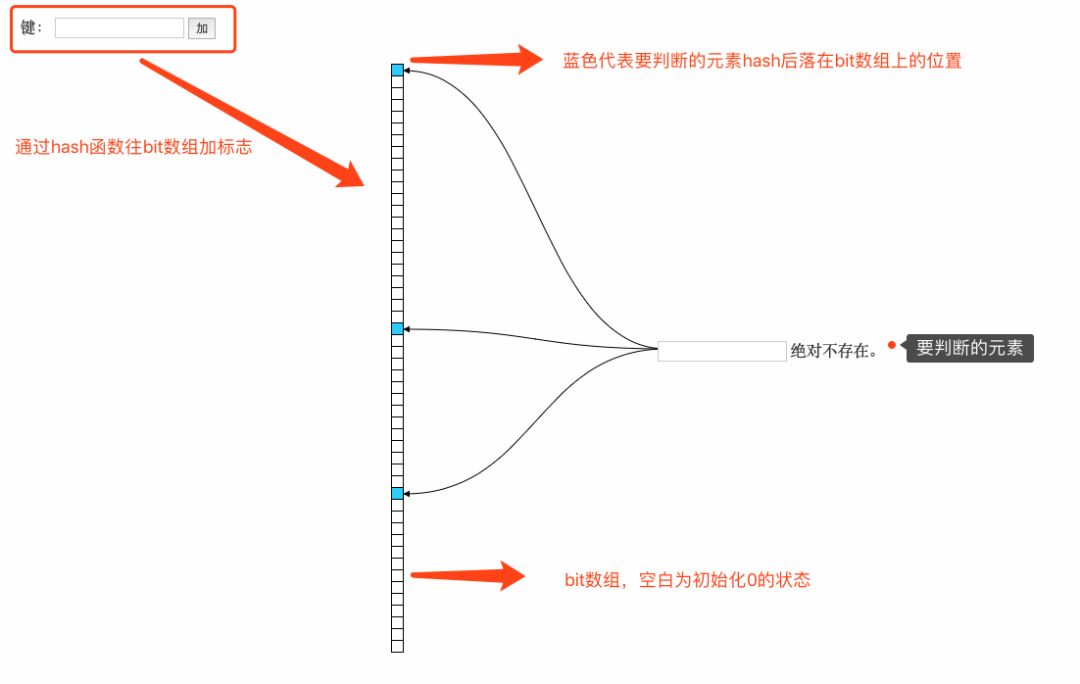
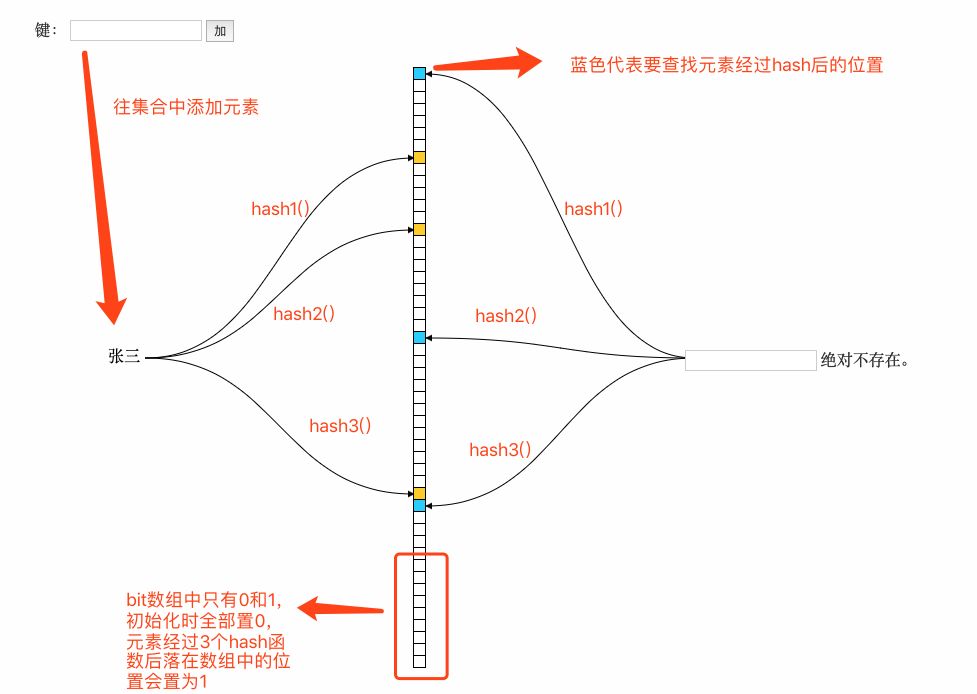
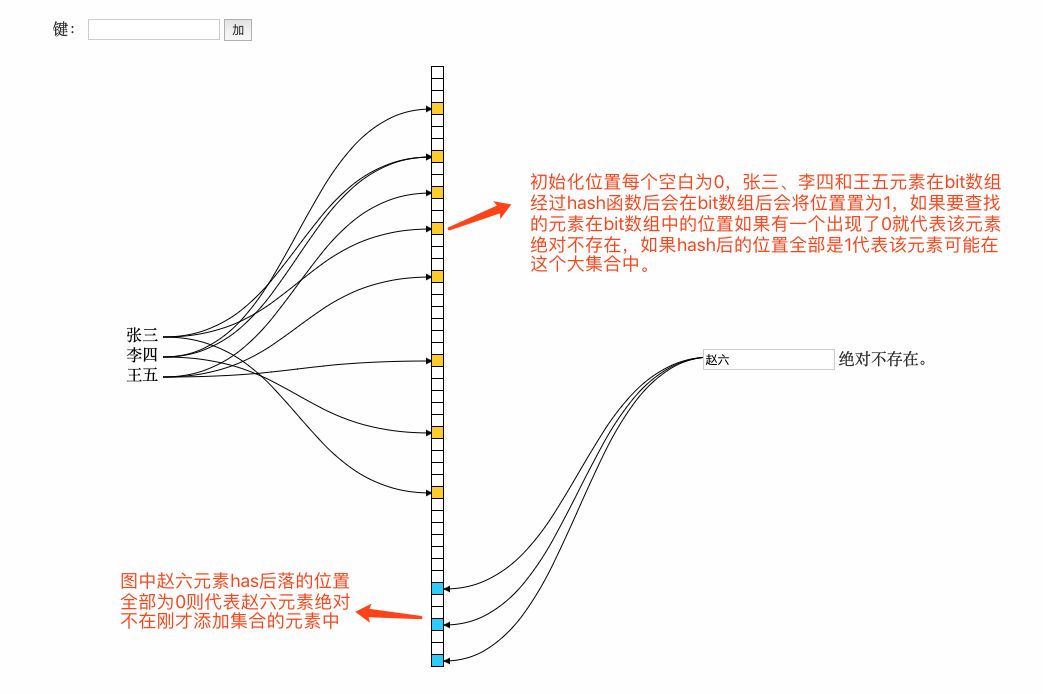
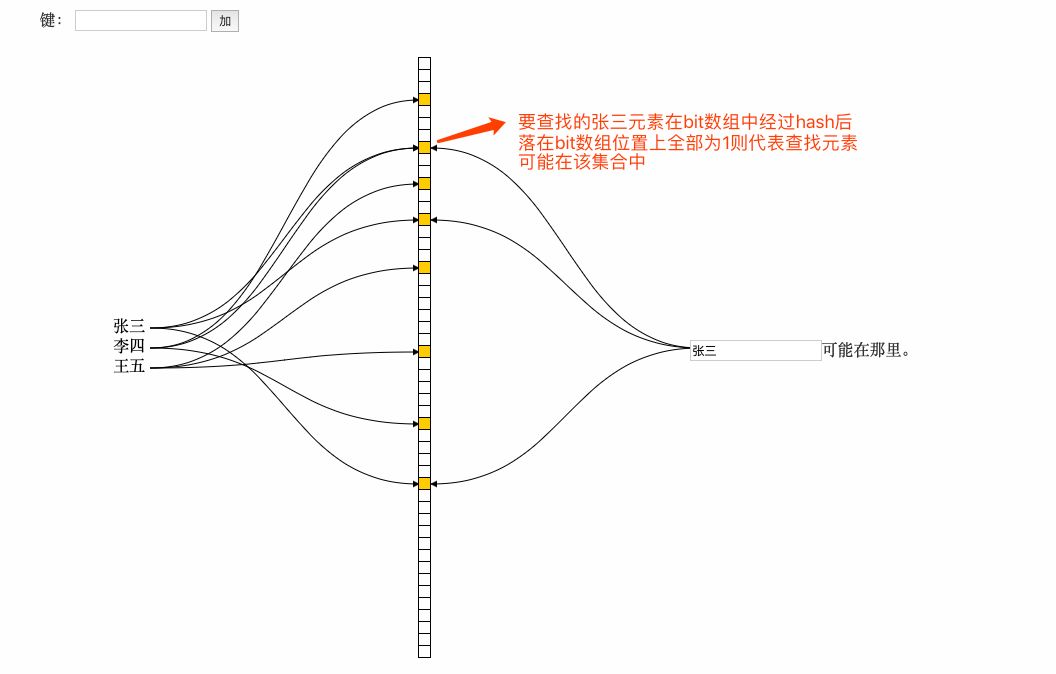
在以上的简单示例中我们可以看到,布隆过滤器本质上是一种比较巧妙的概率型数据结构,可以比较高效的插入和查询,而且可以告诉你”要查找的东西一定不存在和可能存在“,它高效而且占用的空间少,但是它的缺点是其返回的结果是概率性的,不确切的,不能告诉你要查找的东西一定在这个集合中。接下来我们抽象的讲解一下布隆过滤器:
(1) 在添加元素时:将要添加的元素给k个哈希函数,得到对应数组上的k个位置,将这k个位置置为1。
(2)在布隆过滤器查询元素时,将要查询的元素给k个哈希函数,得到对应数组上的k个位置,如果k个位置上有1个为0,则肯定不在集合中,如果k个位置全部为1,则可能在集合中。下面展示一段java代码片:
package com.lab.solr.util;
import java.util.BitSet;
/**
* @description: 布隆过滤器
* @author: zhengshangchao
* @date: 2019-02-17 12:31
**/
public class SimpleBloomFilter {
/**
* 布隆过滤器的长度定义为2的24次方
*/
private static final int DEFAULT_SIZE = 2 << 24;
/**
* 哈希函数的随机种子
*/
private static final int[] seeds = new int[]{7, 11, 13, 31, 37, 61,};
private BitSet bits = new BitSet(DEFAULT_SIZE);
private SimpleHash[] func = new SimpleHash[seeds.length];
/**
* 构造函数初始化哈希函数
*/
public SimpleBloomFilter() {
for (int i = 0; i < seeds.length; i++) {
func[i] = new SimpleHash(DEFAULT_SIZE, seeds[i]);
}
}
/**
* 往bit数组里新增元素的哈希标志位
*
* @param value
*/
public void add(String value) {
for (SimpleHash f : func) {
bits.set(f.hash(value), true);
}
}
/**
* 判断要查询的元素的标志位是否在bit数组中
*
* @param value
* @return
*/
public boolean contains(String value) {
if (value == null) {
return false;
}
boolean ret = true;
for (SimpleHash f : func) {
ret = ret && bits.get(f.hash(value));
}
return ret;
}
/**
* 哈希函数静态内部类
*/
public static class SimpleHash {
private int cap;
private int seed;
public SimpleHash(int cap, int seed) {
this.cap = cap;
this.seed = seed;
}
/**
* 哈希函数
*
* @param value
* @return
*/
public int hash(String value) {
int result = 0;
int len = value.length();
for (int i = 0; i < len; i++) {
result = seed * result + value.charAt(i);
}
return (cap - 1) & result;
}
}
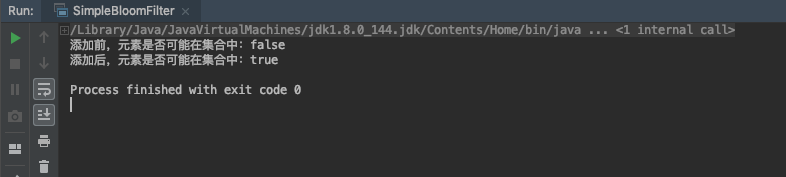
public static void main(String[] args) {
String value = " zhengshangchao@icloud.com";
SimpleBloomFilter filter = new SimpleBloomFilter();
System.out.println("添加前,元素是否可能在集合中:" + filter.contains(value));
filter.add(value);
System.out.println("添加后,元素是否可能在集合中:" + filter.contains(value));
}
}运行结果:
这里我们要注意到,布隆布隆器是不支持删除的,如果一旦删除其中一个值,就会将其hash后的位置上置为0,如果该位置恰好有另外一个位置也置为1,则会出现误判的问题。布隆过滤器的长度会影响误报率,布隆过滤器越长则误报率越小,哈希函数的个数越多,则误报率越小,但效率也越低,但如果太少的话,误报率就会变的很高。
下面我们会有一个公式来算数据量多大时应该对应多长的布隆过滤器和多少个哈希函数的个数。假设k为哈希函数的个数,m为布隆过滤器的长度,n为插入元素的个数,p为误报率。则公式如下:
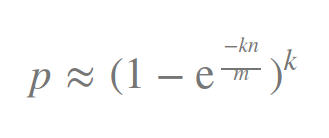

在常用的实践中,由于Redis天然支持setbit和getbit的操作且纯内存操作性能高,所以可以作为理想的布隆过滤器来使用,关于Redis使用布隆过滤器会出现大Value拆分问题,下期将会补充一份技术博客来围绕这个问题进行描述和实践。







