目录
1 特征交叉模型总结
2 特征交叉的业务应用和思考
2.1 模型应用和效果分析
2.1.1 deepFM
2.1.2 DCN
2.1.3 DCN-V2
2.1.4 xDeepFM
2.1.5 PNN
2.2 特征交叉思考
2.2.1 DCN如何实现field-wise特征交叉
2.2.2 deepFM特征交叉结果表征方式
2.2.3 自动高阶特征交叉效果一定好吗
2.2.4 人工先验经验的重要性
1 特征交叉模型总结
推荐模型的效果受几方面的因素影响:样本、特征、模型、工程。
样本是最基本的,影响非常大,样本量的大小对模型的训练效果有直接的影响,当样本量非常大时,可以出现大力出奇迹的效果,这时候即使模型非常简单,也可以达到不错的效果。
特征是训练数据的信息表达载体,直接决定了模型可以挖掘到什么信息,决定了模型效果的上限。在前深度学习时代,模型简单,因此想让模型挖掘出有效的信息,对特征工程的依赖强。深度学习在推荐领域的落地,加强了模型对特征的学习能力,但因为DNN处理的特征空间非常高维,在实际学习过程中想要收敛到理想状态,会面临各种各样的难题,因此不能迷信DNN可以在任何情况下都达到理想状态。当给模型提供越多有效经过先验设计的信息,模型在收敛过程越容易接近最优解。
在推荐数据中,特征之间存在关联模式。虽然DNN可以通过隐式方式学习这些模式,但想在实际过程中学到理想状态,是有难度的,绝大多数情况会陷在某个离最优解有段距离的地方,因此通过人工手工交叉设计,或者通过模型结构进行显式特征交叉,可以使模型学习过程更容易,同时也学到更接近最优解的状态,从而提高模型效果。
模型本身对效果的提升,相对样本和特征而言,比较有限。它的作用是尽可能地捕捉和学习样本和特征里包含的信息,本质上是在不断接近效果的上限。
工程上的实时性对模型效果又直接影响,通过提高模型的实时性,可以让模型更灵敏地捕捉到用户行为背后的兴趣变化。
特征交叉的实现方式不同,对模型效果影响的来源维度也不同,手工设计的交叉特征是从特征层影响,直接从源头上影响;通过设计模型结构实现特征交叉,是从模型层面影响,让模型更充分地挖掘特征背后的信息。这个主题介绍的若干模型,这两种方式都有涉及。
往期分享的特征交叉模型结构包括三个系列:
LR系列,模型包括LR,wide&deep(简写为W&D)
FM系列,模型包括FM、FFM、AFM、FwFM、FNN、PNN、NFM、deepFM
DCN系列,模型包括DCN、DCN-V2、xDeepFM
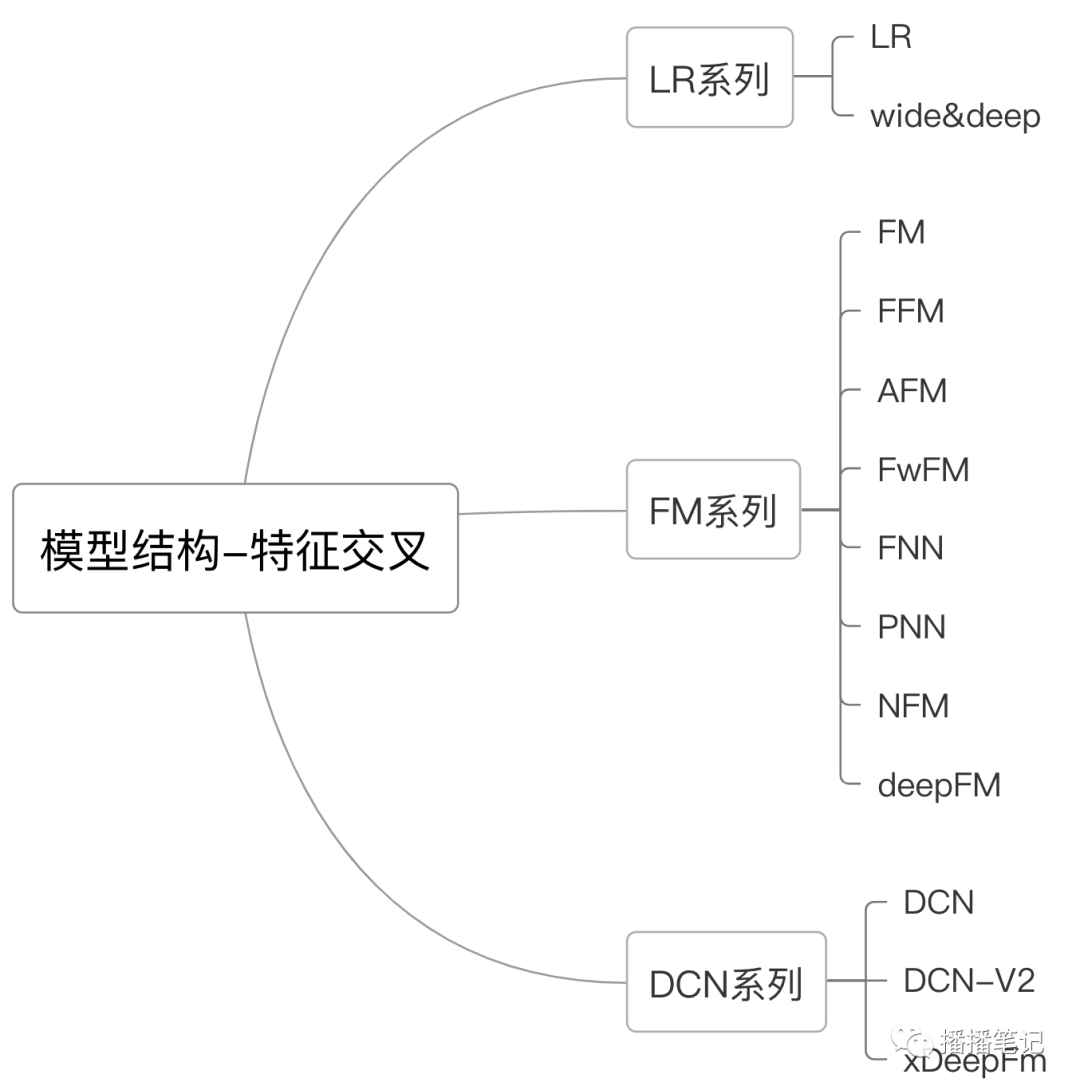
图1 特征交叉模型结构分类
LR系列模型的特征交叉,依赖人工设计,但这个系列的模型LR和W&D在推荐领域有非常重要的地位。LR是前深度学习时代使用最广泛的模型,它原理简单、可解释性强。W&D为后续模型在特征交叉上的优化提供了模型结构的设计思路,即特征交叉结构和DNN结构并行,最后输出层结合这两部分,这种设计思路在特征交叉模型结构的优化上被广泛使用。
FM系列模型,实现了特征的自动交叉,不需要依赖人工设计交叉特征,考虑了特征的field信息,进行field-wise的交叉。这一系列的模型思路相似,在FM的基础上进行两种改进:(1) 在特征交叉中对各个组合项引入差异化,包括FFM、AFM、FwFM;(2) 将FM和DNN结合,包括FNN、PNN、NFM、deepFM。
DCN系列模型,通过模型结构设计,实现特征的高阶显式自动交叉,提高了特征交叉的表达上限。DCN系列模型中,DCN、DCN-V2实现了bit-wise的特征交叉,xDeepFM实现了field-wise的特征交叉。
表1 三种系列模型特征交叉结构对比
模型 | 优点 | 缺点 |
LR系列 | 模型简单,可解释性强 | 依赖人工设计,对特征工程要求高 |
FM系列 | 特征显式自动交叉,不需要依赖人工设计 | 一般交叉到2阶为止,高阶交叉复杂度高 |
DCN系列 | 特征高阶显式自动交叉 | 模型复杂度高 |
表2 模型特征交叉结构特点和复杂度(复杂度仅针对特征交叉结构)
模型 | 优点 | 缺点 | 空间复杂度 | 时间复杂度 |
LR | 模型简单、可解释性强 | 需人工设计交叉组合 | O(N) | O(N) |
W&D | 特征交叉和DNN结合 | 需人工设计交叉组合 | O(N) | O(N) |
FM | 自动交叉,field-wise | 一般到2阶交叉为止 | O(ND) | O(ND) |
FFM | 充分考虑域和域之间的差异性 | 空间复杂度高,一般到2阶为止 | O(FND) | O(DNN) |
AFM | 采用attention机制学习每个组合项的重要度 | 特征组合稀疏性问题 | O(ND) | O(NND) |
FwFM | 考虑隐向量基于域的差异性,参数量比FFM小 | 一般到2阶为止 | O(ND+FF) | O(DNN) |
FNN | FM作为DNN输入,发挥FM优势 | 分段训练(非end-to-end);FM作为底层输入,作用被削弱;FNN的模型能力受FM能力限制 | O(ND) | O(ND) |
PNN | end-to-end结合显式交叉和DNN结构 | 内积/外积交叉计算复杂度高;显式交叉作为DNN输入导致低阶交叉重要度降低 | 内积形式O(NNH) | 内积形式 O(NND+NNH) |
NFM | 结合FM和DNN,保留了低阶交叉信息;用向量而非标量表达二阶交叉 | 二阶交叉作为DNN输入,交叉特征隐式化 | O(ND) | O(ND) |
deepFM | 结合FM和dnn,field-wise | 交叉到2阶为止 | O(FD) | O(FD) |
DCN | 高阶显式交叉 | bit-wise | O(2NL) | O(LNN) |
DCN-V2 | 高阶显式交叉,交叉项feature map有差别加权组合,可引入非线性优化 | bit-wise,参数量增加 | O(LNN) | O(LNNN) |
xDeepFM | 高阶显式交叉,field-wise | 时间复杂度高 | O(2LHDF) | O(FHHDL) |
N为输入特征
2 特征交叉的业务应用和思考
DNN结构通过全连接层和激活函数,实现了特征的隐式高阶交叉。理论上DNN结构可以学到特征之间的交叉模式,但DNN在高维空间收敛到最优解在实际过程中实现起来有难度,因此在模型中输入先验的特征交叉信息,或者通过网络结构的设计使特征显式自动交叉,可以降低模型的学习难度,从而达到更好的效果。
我在实际业务中尝试过多种模型,其中有一些有显著效果,有一些有不显著效果。
2.1 模型应用和效果分析
2.1.1 DeepFM
DeepFM优化W&D,有明显效果,且为后续优化提供了一个比较强的base。
2.1.2 DCN
DCN对比DeepFM在某些业务有明显效果,在某些业务效果不明显。从效果说明了deepFM中FM这个结构很强。DCN效果不明显,有两方面的思考:
(1) bit-wise的交叉和field-wise对比,由于没有考虑到field信息,效果打折,这里有兴趣的朋友可以试一试,把DCN的交叉结构层数设为1,其它部分DCN和deepFM两个模型保持一致,再对比效果;
(2) 通过增加模型层数,使其学习高阶特征交叉,是预期想达到的理想状态,但是同时带来模型复杂度的提高,以及模型学习难度的提高,在实际过程中,模型是否能学到期望的效果,是存疑的,这点也不太好验证,目前我没有想到一个比较好的验证方式,或许可以试试不同的特征交叉层数。
2.1.3 DCN-V2
DCN-V2对比DCN/deepFM有明显提升,但需要比较好的工程支持,否则容易由于模型空间复杂度和时间复杂度过高,线上推理超时,无法满足服务部署要求。
DCN-V2的效果,个人认为属于大力出奇迹的这种,通过大量增加模型参数(相比DNN侧),来提高模型表达能力,达到提高模型表达能力的效果。
2.1.4 xDeepFM
从离线指标看,对比deepFM有微弱提升,由于线上服务耗时问题,没有部署线上。个人觉得需要看业务,也许有的业务会和DCN一样有提升,但这部分提升,个人也认为是大力出奇迹的这种。
2.1.5 PNN
在具体业务中使用PNN落地,仅使用PNN的交叉部分,用于替换deepFM中的FM部分,对交叉后的向量进行线性组合,得到交叉特征表征。相比deepFM,有不显著的提升。这里的提升,主要来源于通过引入矩阵参数对交叉项组合,一定程度提高了信息量,但这个提升有限,进一步说明了FM对特征交叉的强大性。
2.2 特征交叉思考
在特征交叉这个主题的系列分享中,遗留了一些问题,在这里解答部分,没有解答的会在后续相关主题中继续。
2.2.1 DCN如何实现field-wise特征交叉
DCN模型实现的是bit-wise的特征交叉,忽略了特征的field信息,是否可以借鉴DCN的bit-wise交叉的思路,实现field-wise的交叉呢?
应该是可以的,对于输入从N维的特征
我在具体业务落地时,和deepFM相比有一定效果,但效果不如DCN-V2,还是那句话,DCN-V2属于大力出奇迹这类效果。
代码1 DCN field-wise特征交叉
def dcn_cross_layer_field_vector(params, input_layer, mode, layer_dropout=1):'''cross net module: field-wise cross, w use vectorx_{l+1} = x_0*(tf.matmul(W_l, x_l) + b_l) + x_l'''layer_name = 'cross_layers_field_v'field_num = input_layer.shape[1].value # return the F number input_layer [B, F, D]ebd_dim = input_layer.shape[2].value # the embedding size of each field, in this model, the size of all fields is sameoutput_size = params.cross_layers['out_dim']layer_num = params.cross_layers['layer_num']kernel_initializer = tf.glorot_uniform_initializer()bias_initializer = tf.zeros_initializer()embedding_layer_0 = tf.transpose(input_layer, [0, 2, 1]) # [B, D, F]embedding_layer_extend_0 = tf.expand_dims(embedding_layer_0, axis=3) # [B, D, F, 1]embedding_layer_l = embedding_layer_0 # [B, D, F]tf.logging.warning("{} input shape: {}".format(layer_name, input_layer.shape))# process cross netfor i in range(layer_num):index = i + 1embedding_layer_extend_l = tf.expand_dims(embedding_layer_l, axis=2) # [B, D, 1, F]kernel = tf.get_variable(name="{0}_kernel_{1}".format(layer_name, index),shape=[field_num, 1],dtype=tf.float32,initializer=kernel_initializer,) # [F, 1]bias = tf.get_variable(name="{0}_bias_{1}".format(layer_name, index),shape=[ebd_dim, field_num],dtype=tf.float32,initializer=bias_initializer,) # [D, F]embedding_layer_m_0_l = tf.matmul(embedding_layer_extend_0, # [B, D, F, 1]embedding_layer_extend_l, # [B, D, 1, F]name="{0}_m_0_l_{1}".format(layer_name, index),) # tf.matmul(x_l, W_l) [B, D, F, F]embedding_layer_m_0_l_w = tf.matmul(embedding_layer_m_0_l, # [B, D, F, F]kernel, # [F, 1]name="{0}_m_0_l_w_{1}".format(layer_name, index),) # [B, D, F, 1]# for matrix: embedding_layer_l = tf.add(tf.add(tf.reduce_sum(embedding_layer_m_0_l_w, axis=2, keepdims=False), bias), embedding_layer_l) # 【B, D, F】embedding_layer_l = tf.add(tf.add(tf.squeeze(embedding_layer_m_0_l_w, axis=[3]), bias),embedding_layer_l) # [B, D, F]if layer_dropout < 1.0:embedding_layer_l = tf.layers.dropout(embedding_layer_l, rate=(1 - layer_dropout),training=(mode == tf.estimator.ModeKeys.TRAIN),name="{0}_layer_{1}_dropout".format(layer_name, index),)# process outputembedding_layer_l = tf.squeeze(tf.concat(tf.split(embedding_layer_l, field_num, axis=2), axis=1),axis=[2]) # [B, F*D]# concate 输出output_w = tf.get_variable("{0}_output_w".format(layer_name),shape=[field_num * ebd_dim, output_size],dtype=tf.float32,initializer=kernel_initializer,)output_layer = tf.matmul(embedding_layer_l, output_w, name="{0}_output".format(layer_name)) # [B, Output]return output_layer
2.2.2 deepFM特征交叉结果表征方式
deepFM的特征交叉,可以在D和F两个维度求和,从而得到不同维度的表征,两种表征方式可能存在信息量不等价问题。在D这个维度求和相当于对F个field特征两两内积,得到F*(F-1)/2维的向量表征,而采用计算优化方式,相当于在field维度求和,则得到D维向量表征。
具体问题在《模型结构之特征交叉(2)-FM系列(2.2)-AFM,DeepFM等(附代码)》有详细说明,其中附了在field维度求和的代码,当时写该篇分享时还没有验证,对两种表征方式没有明确结论,只是猜想用D维表征特征交叉结果,不会有明显效果。
后来做了一些其它改进,加了一些交叉项,也就是使用内积求和方式,得到f维(指定f种交叉)的向量表征,有明显效果提升;而使用优化方式,最终得到D维向量表征,对比base没有明显变化。因此推测内积形式得到的F*(F-1)/2维的向量表征,具备更强的信息量。F*(F-1)/2维的结果表征,相当于对交叉操作先按位乘然后sum pooling,结果再concat,而D维的结果表征,相当于交叉操作先按位乘,再sum pooling;两者对比,在每个交叉项内sum pooling后concat,比对所有交叉项之间sum pooling,信息表达能力更强,也就是在项内sum pooling使信息表达更合理。
关于这个点,可能我的想法也不对,欢迎朋友一起来讨论。
2.2.3 自动高阶特征交叉效果一定好吗
在理想情况下,特征自动高阶交叉,其信息表达能力肯定强于手工低阶交叉的表达能力,但在具体业务场景和实际模型训练过程,可能不一定。我在尝试特征自动高阶交叉时,便遇到了这个问题。
分析可能的原因有两点:
(1) 模型自动高阶特征交叉时,模型复杂度提高,导致模型学习难度增加,在实际收敛过程,不一定能收敛到预期的效果;这点可以通过拉长时间和加大数据量解决,但不好论证;
(2) 模型自动交叉项中的某些项带偏了,这些项实际上可能没有交叉性,但在少量数据上表现出强交叉性,而在大多数数据上没有,但模型被这少量数据带偏后纠不回来了;关于这点,也比较难论证且存疑,因为默认模型是学数据分布的某个函数,如果某些交叉项在大多数数据上没有,那模型就不应该学到,学偏后是否能纠回来,默认是可以的。
2.2.4 人工先验经验的重要性
我在特征交叉的优化上,让模型显式自动高阶特征交叉,某些模型的效果不及预期,而通过人工对业务的分析,加入一些手工交叉特征,效果非常明显,再次论证了人工先验经验的重要性,以及算法工程师的必要性。
神经网络理想状态下很强大,可以拟合任何函数,但很多时候会因为它理论的强大忽略一点:它的学习是有难度的。算法工程师不断挖掘先验知识,输入到模型,可以非常有效降低模型学习难度,使模型更接近预期的理想状态。
模型不是万能的,一个好的算法工程师,其作用之一是让模型效果不断接近它的天花板。
下一篇将分享多目标、激活函数或者其它。
以及朋友们有什么想要一起探讨的,可以在评论区告诉我,共同学习一起进步呀~
推荐系列文章:
推荐模型结构-特征交叉
基础知识类
工具类
微信最近对公众号的推送算法改版较大,为了更好地找到我,动动手对这个公众号置顶呀~
公众号的内容会同时在知乎专栏更新,有兴趣的朋友可以在知乎找我玩(知乎账号:婷播播),知乎专栏:推荐学习笔记。
生活的思考和记录会在另一个公众号更新,有兴趣的朋友也可以动手关注一下






