为什么DCN可以实现显式高阶特征交叉-模型结构之特征交叉(3)-DCN系列(3.1)附代码

播播笔记 2022-04-09

1025

前面几篇文章介绍了通过模型结构进行特征交叉的LR系列和FM系列，包含LR、wide&deep，FM、MF、FFM、AFM、FwFM、FNN、PNN、NFM、DeepFM多个模型，想回顾的朋友可以移步到《模型结构之特征交叉(1)-从LR到wide&deep》、《模型结构之特征交叉(2)-FM系列(2.1)-FM,FFM》、《模型结构之特征交叉(2)-FM系列(2.2)-AFM,DeepFM等(附代码)》。本文将介绍第三种模型系列，即DCN系列。

基于FM思想的特征交叉，解决了LR时代手动特征交叉对人工经验的依赖以及交叉不全面的问题，但由于特征的高维度，FM往往止步于二阶交叉，一方面是因为二阶交叉可以取得不错的效果，另一方面是因为当阶数增加时，交叉项的数量以指数形式增长，导致参数量的指数增长，而且此时FM无法使用二阶交叉时的计算优化方法，时间复杂度也随之指数增加。可见FM虽然让显式特征交叉摆脱了对人工设计的依赖，但难以实现更高阶的显式特征交叉，而实际推荐领域的数据非常复杂，其中一定包含特征之间高阶交叉模式，如果通过模型结构设计，帮助模型高效捕捉这些模式，将提高推荐结果的准确性，因此DCN系列模型相继提出。

DCN系列模型，其结构包括两部分，特征交叉(Cross Net)模块和DNN模块，如图1所示。特征交叉模块通过多层网络对特征向量的加和乘处理，实现特征的显式高阶交叉，其输出和DNN模块的输出结合，得到结果。本文将分享DCN模型，DCN-V2、xDeepFM后续将陆续分享。

1 DCN

1.1 DCN原理
1.2 特征交叉层
1.3 如何理解DCN特征交叉

1.3.1 特征L+1阶交叉

1.3.1.1 归纳法理解
1.3.1.2 具体例子

1.3.2 参数w的理解
1.3.3 DCN的优缺点

1.4 特征交叉代码实现

1.4.1 实现优化
1.4.2 代码

相关面试问题

特征交叉的目的是找到特征关联的模式，在所有的特征组合里，有的对模型贡献大，有的对模型贡献小，其重要性存在差异。这种差异不同于特征取值不同导致组合结果不同带来的差异，特征本身值的不同带来的差异性是特征本身的差异，而特征组合的重要性差异，和特征值的大小没有关系，只是和某种组合关系相关。举个例子，当数据中运动这类特征和音乐这类特征存在明显的关联性，而运动这类特征和外貌这类特征关联性不强时，则在特征交叉时，特征组合为<运动类特征，音乐类特征>的重要性要高于<运动类特征，外貌类特征>，对模型的贡献程度存在差异。

图1 DCN系列模型结构框架

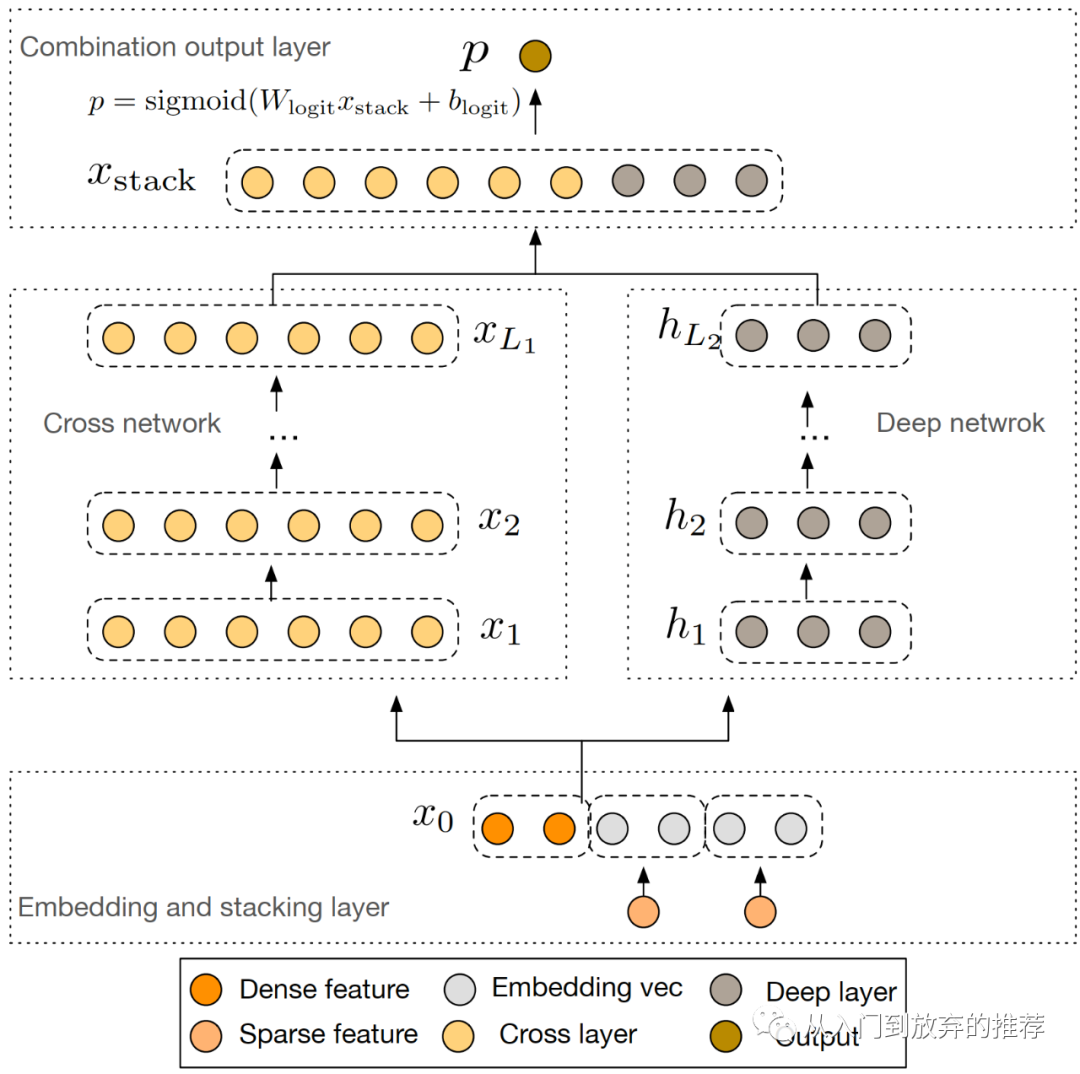
特征的高阶交叉

继续以前几篇文章里提到的运动和音乐为例，再加上年龄这类特征，它们之间的交叉为三阶交叉，即[年龄、运动、音乐]。数据里存在一些三阶交叉模式，比如[13-18岁、篮球、Rap]这种组合，在数据中比较常见，而[0-5岁、篮球、Rap]这种组合，在数据中则比较少见。

当特征里再加上性别这类特征，则可以形成四阶交叉，即[性别、年龄、运动、音乐]，[男、13-18岁、篮球、Rap]这种组合在数据中比较常见，而[女、13-18岁、篮球、Rap]这种组合，在数据中则比较少见。

1 DCN

Deep & Cross Network[1](DCN)出自论文《Deep & Cross Network for Ad Click Predictions》，由斯坦福和谷歌联合发表于AdKDD 2017。DCN是谷歌对wide&deep工作的延续，模型结构的思想和wide&deep相同，分为deep侧和特征交叉侧，但它通过对特征交叉侧的模型结构设计，巧妙地实现了特征bit-wise的高阶交叉，提出了一种显式高阶特征交叉的思路，被后续各种基于特征显式高阶交叉优化的方法采用。

1.1 DCN原理

DCN的网络结构如图2所示，包括左侧的特征交叉网络和右侧的DNN两部分，两部分的输出结合后再得到模型最终结果，论文采用的结合方式是直接concat。损失函数为交叉熵损失，为了防止过拟合，可以在损失函数中加上正则项。模型训练采用联合训练的方式，和wide&deep的类似，具体细节在《模型结构之特征交叉(1)-从LR到wide&deep》已介绍。

图2 DCN模型结构

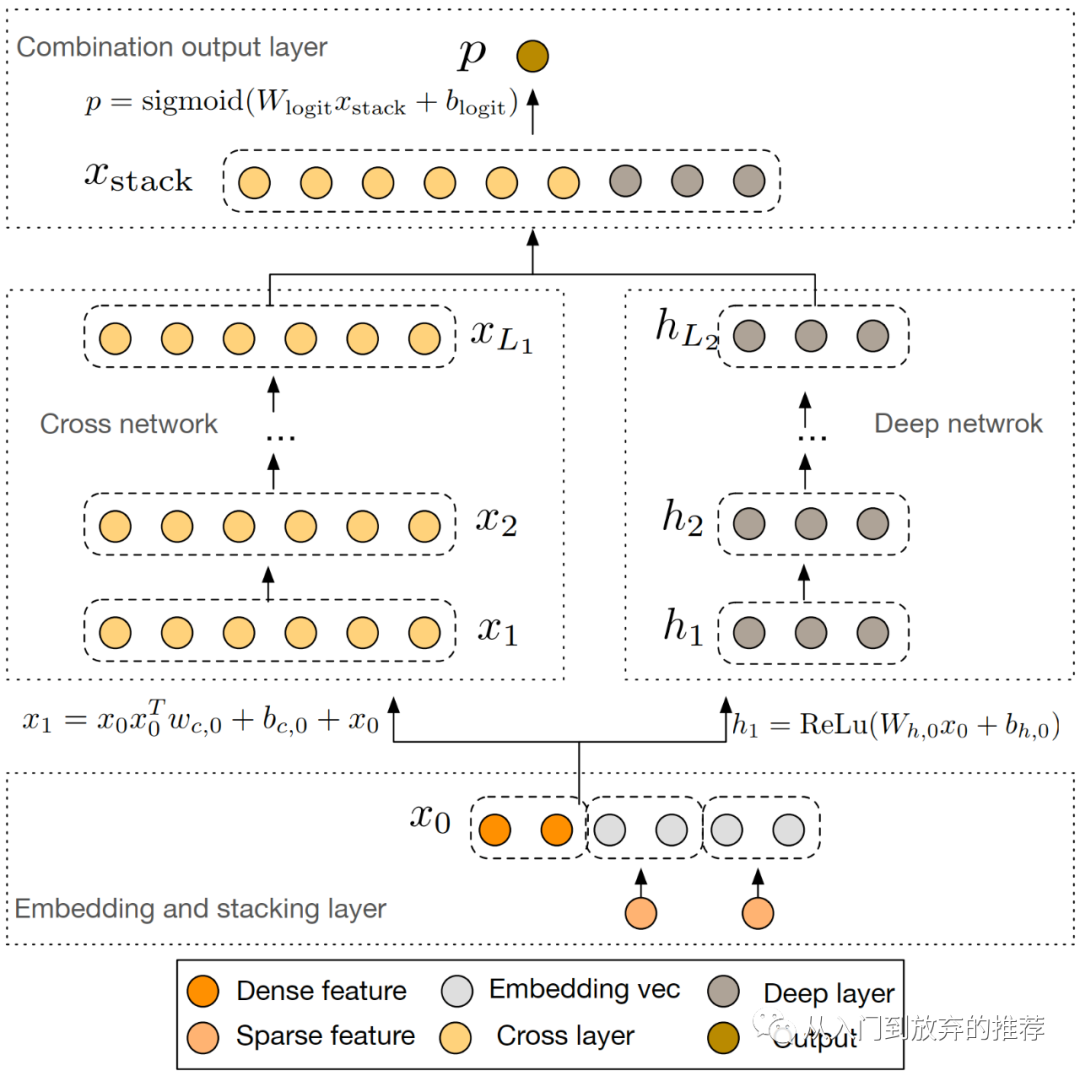
DCN核心创新点在于cross net的网络结构设计，特征向量经过多层网络，进行向量加和乘的操作，实现高阶交叉。

1.2 特征交叉层

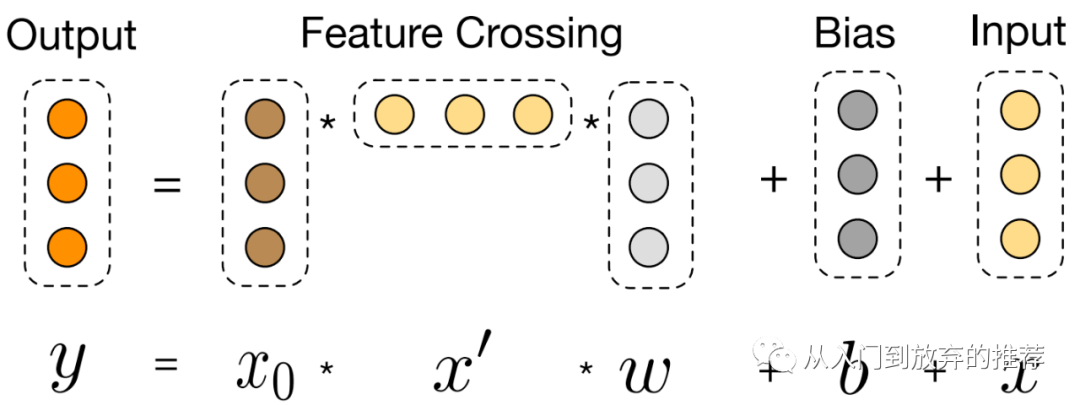
特征交叉层对特征进行显式的交叉操作，如式子(1)和图3所示，核心包括两部分：(1) 和相乘；(2) 相乘结果和相加。经过L层特征交叉层后，将得到L +1阶交叉特征。特征交叉层引入了残差的思想，每层函数f拟合和的残差，残差网络有利于缓解梯度消失的问题，从而使网络具备更深的深度。

图3 DCN特征交叉层

特征交叉层的设计很巧妙，使得：

(1)每一层的输入输出保持相同的形状，从而使网络参数随着网络层数呈线性增长；
(2) 特征的交叉阶数由网络深度决定，即交叉特征的阶数和网络层数一致；
(3) 特征交叉网络的输出，包含了从1阶(特征本身)到L+1阶的所有特征交叉项组合。

每层的输出特征，其形状和输入特征相同，参数和的形状和输入特征相同，均为N维。当特征交叉层有L层时，网络的参数量为2NL，和网络层数为线性关系。是经过embedding层之后的稠密特征，其维度N不高，因此特征交叉网络通过新增少量参数( )实现了特征的所有维度之间的高阶交叉。

1.3 如何理解DCN特征交叉

特征交叉网络实现了特征的L+1阶交叉，其输出包含了特征从1阶到L+1阶的所有特征交叉项组合，可以用归纳法理解，也可以结合具体例子理解。在特征交叉层的特征乘法操作中，和乘完后得到所有项的特征组合，然后再和向量相乘，理解在其中的作用，可以加深对所有项特征交叉组合的理解。

1.3.1 特征L+1阶交叉

1.3.1.1 归纳法理解

当没有经过交叉层时，输入为经过embedding层的稠密特征，即1阶特征项。

当经过1层特征交叉层时， ( 为偏置项，不影响特征交叉阶数)，包含了所有的2阶交叉组合项，乘以后只是2阶交叉项的系数发生变化；再加上 (1阶所有特征交叉项组合)，此时则包含了1阶到2阶的所有交叉组合项。

当经过2层特征交叉层时，，由于包含了1阶和2阶的所有交叉组合项，因此包含了所有2阶和3阶的交叉组合项，再加上，则包含了所有1阶到3阶的交叉组合项。

以此类推，当经过L层特征交叉层时，，由于包含了1阶到阶的所有交叉组合项，因此则包含了所有2阶到阶的特叉组合项，再加上，则包含了所有1阶到阶的交叉组合项。

1.3.1.2 具体例子

以输入特征是2维为例，即，由于偏置项不影响特征交叉阶数，为了方便将其置0。下面计算和。

可以看出，包含了原始特征从1阶到2阶的所有可能交叉组合项(所有1阶项：，所有2阶交叉组合：。

从式子(3)可以看出，包含了原始特征从1阶到3阶的所有交叉组合(所有3阶交叉组合： )。

结合归纳法和具体的例子一起理解，则更加清晰，每层的乘法操作实现了2阶到阶的所有交叉组合，加上后，则实现了1阶到阶的所有交叉组合。

1.3.2 参数w的理解

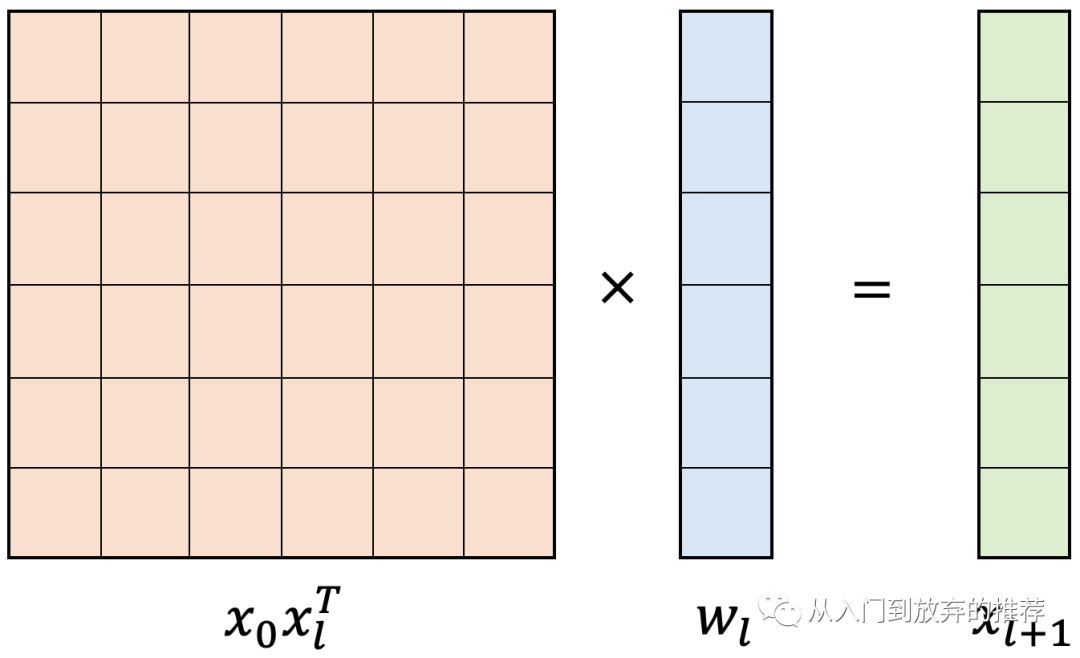
从上一节的具体例子可以看出，对2阶到阶的交叉组合项进行线性组合，如图4所示，形成的feature map(橙色部分所示)，第i行的交叉项和相乘，得到对应的第 i 项。feature map中的所有行(交叉项形成)，共享参数。

图4 特征交叉层f操作示意图

交叉组合共享，有几个优点：(1) 有效地减少了网络的参数量；(2) 提高模型的泛化性，比如，当训练数据中没有出现交叉组合，则对应的权重为0，当测试集中出现这个交叉组合时，则无法进行有效的加权；而共享参数，则可以通过其它交叉组合的出现，学习对应的权重，从而提高泛化能力。

参数的共享，在某些情况下是优点，从另一个角度看也可能是缺点，由于共享，形成的feature map每行进行线性组合时，其差异性无法体现，因此可能使效果打折。基于此，DCN-V2[2]模型被提出。

1.3.3 DCN的优缺点

DCN的网络结构特点，决定了DCN的特点，辩证地看待这些特点，也就成了DCN的优缺点。

优点：

实现了显式的特征交叉，且包含了所有特征交叉组合项，摆脱了对人工设计交叉特征的依赖；
特征交叉的阶数由cross net网络深度决定，灵活可调，一般设为3-4，可根据具体业务调整；
网络参数的增加量小，新增参数复杂度为 O(NL) ，和网络深度呈线性关系。

缺点：

特征交叉为bit-wise，忽略了特征的域信息；

这里留个思考，如何实现field-wise的特征交叉

特征交叉中使用向量参数，使形成的feature map的每行所表征的特征交叉项进行线性组合时，其差异性无法体现。

1.4 特征交叉代码实现

经过前面对DCN的特征交叉层的介绍，其原理已经比较清楚了，式子(1)表示了特征交叉层的操作，根据该式子，可以完成特征交叉网络的实现。

式子(1)涉及到矩阵乘法，运算量比较大，而通过矩阵乘法的结合律可对其进行优化，可有效降低计算量。

1.4.1 实现优化

式子(1)先将 $和$ 相乘后得到的矩阵，再和向量相乘，而通过结合律，先将和相乘，得到一个标量，再用和该标量相乘，如式子(4)所示，则可减少矩阵相乘的计算量。

下面论证优化的等价性，即矩阵乘法的结合律成立，如式子(5)所示，其中 A, B, C 为相乘的矩阵，矩阵A形状为，B形状为，C形状为。

1.4.2 代码

代码1 DCN cross net代码实现

def dcn_cross_net(params, x, mode, layer_dropout=1):
    '''
    Reference: [ADKDD 2017] Deep & Cross Network for Ad Click Predictions
    x_{l+1} = tf.matmul(tf.matmul(x_l, x_0), w_l) + b_l + x_l
    :param params: the model config params
    :param x: raw feature input [B, N]
    :return: [B, N]
    '''


    layer_num = params.cross_layers['layer_num']
    output_size = params.cross_layers['out_dim']


    layer_name = 'cross_layers_vector'
    kernel_initializer = tf.glorot_uniform_initializer()
    bias_initializer = tf.zeros_initializer()


    embedding_layer_0 = tf.expand_dims(x, axis=2)  # [B, N, 1]
    embedding_layer_l = embedding_layer_0  # [B, N, 1]


    input_size = x.shape[1].value  # return the N number


    for i in range(layer_num):
        index = i + 1
        kernel = tf.get_variable(
            name="{0}_kernel_{1}".format(layer_name, index),
            shape=[input_size, 1],
            dtype=tf.float32,
            initializer=kernel_initializer,
        )  # [FD, 1]
        bias = tf.get_variable(
            name="{0}_bias_{1}".format(layer_name, index),
            shape=[input_size, 1],
            dtype=tf.float32,
            initializer=bias_initializer,
        )  # [FD, 1]
        embedding_layer_l_w = tf.tensordot(
            embedding_layer_l,
            kernel,
            axes=(1, 0),
            name="{0}_l_w_{1}".format(layer_name, index),
        )  # [B, FD, 1] * [FD, 1] -> [B, 1, 1]
        embedding_layer_0_l_w = tf.matmul(
            embedding_layer_0,
            embedding_layer_l_w,
            name="{0}_0_l_w_{1}".format(layer_name, index),
        )  # [B, N, 1] , [B, 1, 1] -> [B, N, 1]
        embedding_layer_l = tf.add(tf.add(embedding_layer_0_l_w, embedding_layer_l), bias)  # [B, N, 1]
        if layer_dropout < 1.0:
            embedding_layer_l = tf.layers.dropout(embedding_layer_l, rate=1 - layer_dropout,
                                                  training=(mode == tf.estimator.ModeKeys.TRAIN))


    embedding_layer_l = tf.squeeze(embedding_layer_l, axis=2, name="{0}_squeeze".format(layer_name))  # [B, N]
    # process output
    output_w = tf.get_variable(
        "{0}_output_w".format(layer_name),
        shape=[input_size, output_size],
        dtype=tf.float32,
        initializer=kernel_initializer,
    )
    output_layer = tf.matmul(embedding_layer_l, output_w, name="{0}_output".format(layer_name))  # [B, Output]


    return output_layer