为了方便和上一篇连起来,这一篇的各种标题序号,公式序号,图序号也都延续上一篇。
基于FM的系列模型,在FM的基础上进行改进,基本是从两个角度出发:(1) 挖掘不同的特征组合的重要度差异;(2) 结合FM和dnn两部分,充分结合显式特征交叉和隐式特征交叉的优势。
目录
3 AFM
4 FwFM
5 FNN
6 PNN
6.1 网络结构
6.2 embedding layer
6.3 product layer
6.3.1 线性部分
6.3.2 非线性部分
6.3.2.1 IPPN
6.3.2.2 OPPN
7 NFM
8 DeepFM
相关面试问题
特征交叉的目的是找到特征关联的模式,在所有的特征组合里,有的对模型贡献大,有的对模型贡献小,其重要性存在差异。这种差异不同于特征取值不同导致组合结果不同带来的差异,特征本身值的不同带来的差异性是特征本身的差异,而特征组合的重要性差异,和特征值的大小没有关系,只是和某种组合关系相关。举个例子,当数据中运动这类特征和音乐这类特征存在明显的关联性,而运动这类特征和外貌这类特征关联性不强时,则在特征交叉时,特征组合为<运动类特征,音乐类特征>的重要性要高于<运动类特征,外貌类特征>,对模型的贡献程度存在差异。
基于FM模型改进的另一种角度,是将FM和DNN结合。上一篇介绍的FM、FFM、以及第一种思路的改进AFM、FwFM,都是基于LR模型的框架,而DNN已经在CV、NLP等领域验证了它对特征提取的有效性,因此将其应用到推荐领域,是几年前的趋势。NFM、FNN、PNN、DeepFM等模型,正是在这种趋势下提出的。
3 AFM
AFM[5] 出自论文《Attentional Factorization Machines: Learning the Weight of Feature Interactions via Attention Networks》,发表于IJCAI2017。
AFM通过使用attention的思路,对不同特征组合赋予个性化的权重。特征交叉部分的网络结构如图4所示。非特征交叉的部分和FM相同。
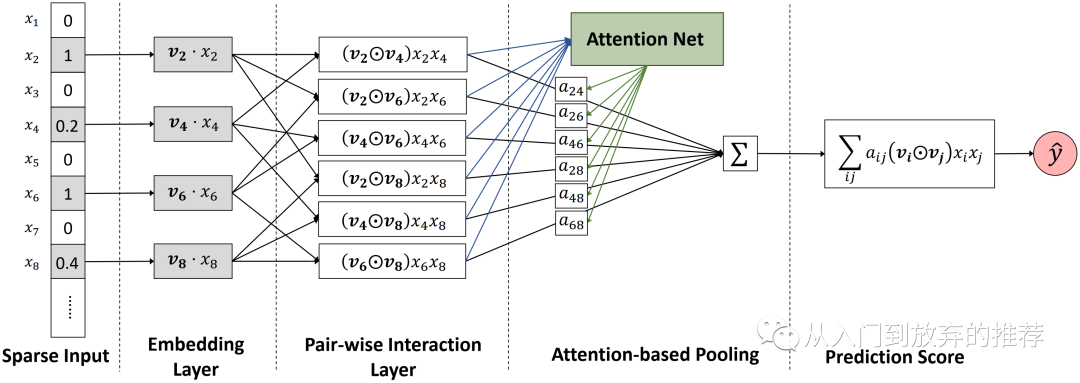
图4 AFM特征交叉部分网络结构
AFM利用attention net,学每组特征组合的权重,该特征组合项作为attention net的输入,决定了该权重大小。如式子(16)所示,attention net的输入是当前特征组合的哈达玛积形式,是一个K维的向量,其中
哈达玛积:两个形状相同的矩阵,元素按位相乘得到的矩阵。
AFM提出了一种很好的思路,即利用attention机制学习不同特征组合的重要度,对不同用户而言,其重要度理论上是存在差异的,后续快手提出的poso网络,其思路和AFM的思路是相同的,这种对网络结构的改进,对用户活跃度相关的问题是一个比较好的思路。
4 FwFM
FwFM[6] 出自论文《Field-weighted Factorization Machines for Click-Through Rate Prediction in Display Advertising》,发表于WWW2018。
FwFM是基于FFM的改进,FFM的每维特征对每个域会对应生成一个隐向量,因此空间复杂度高。为了保持每维特征在特征组合时对不同域的差异性,同时又保持较小的空间复杂度,FwFM使用了一组参数描述所有域的组合的重要性。
式子(18)表示了FwFM模型。通过引入一组参数
AFM和FwFM是从特征交叉重要度的角度,在FM的基础上进行改进。在FM系列模型中,显式交叉的特征一般都只使用到二阶为止,构建更高阶的交叉会导致参数量呈数量级的增加,使计算量变大。而实际上特征之间的关联性非常复杂,至少比二阶复杂,因此需要比手工交叉更方便的形式,来获取特征之间更高阶的交叉性,这也是基于FM优化的另一种角度,即结合FM显式特征交叉和DNN隐式高阶特征交叉,使模型对特征的提取更充分,因此FNN、PNN、NFM、DeepFM等模型相继被提出。
5 FNN
FNN[7] 出自论文《Deep Learning over Multi-field Categorical Data – A Case Study on User Response Prediction》,发表于ECIR2016。
FNN的思路简单直接,将FM作为DNN的输入,利用DNN继续进行特征的高阶隐式交叉。
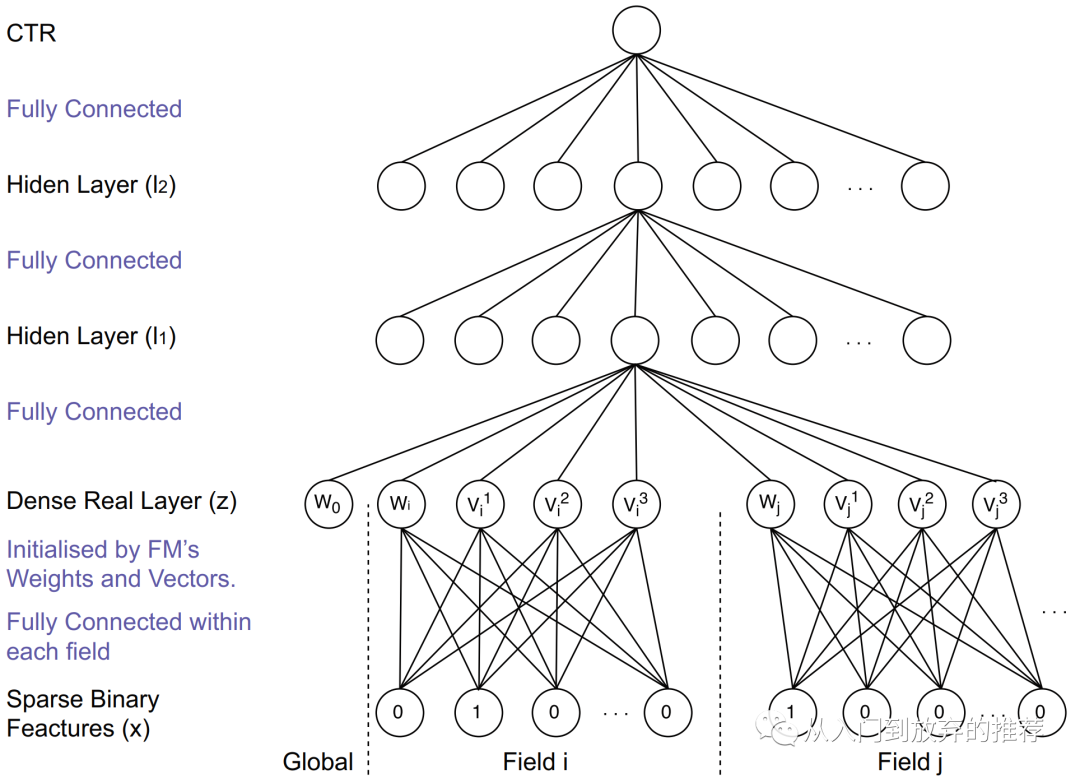
图5 FNN网络结构
FNN的求解和DNN网络的求解相同,针对当前应用问题定义损失函数,基于梯度下降法求解参数。
FNN将FM和DNN对特征学习的能力结合起来,为后续DNN在推荐领域的模型优化提供了一种思路。
另一方面,FNN也存在一些问题:
(1) 采用分阶段的训练方式而不是end-to-end的方式,有损实现过程的方便性;
(2) FM的训练结果作为FNN的底层输入,导致FNN的模型能力受限于FM学到的特征表达的上限;
(3) 在网络反向传播时,经过几层DNN,容易导致FM的信息被削弱;
(4) FNN通过DNN进行特征的高阶隐式交叉,忽略了特征的低阶交叉信息,FM学到的信息作为输入。
6 PNN
PNN[8] 出自论文《Product-based Neural Networks for User Response Prediction》,发表于ICDM2016。
PNN通过网络结构设计,在网络低层实现了类似FM的特征交叉,再连接dnn学习特征的高阶交叉性,从而实现FM和DNN的结合。
6.1 网络结构
推荐领域的特征类别特征非常多,one-hot的表征方式导致特征高维稀疏,特征空间的巨大使得特征的one-hot的表达形式,无法直接应用到dnn,FNN采用的是预训练FM解决这个问题,PNN采用了另一种方法,使用embedding layer,将高维稀疏的特征转化为低维稠密的表征。在显式特征交叉部分,PNN沿用了FM的思想,在网络结构中引入product layer,对特征进行线性组合以及低阶显式交叉,得到特征表征后,连接到dnn进行隐式高阶交叉。PNN的网络结构如图6所示。
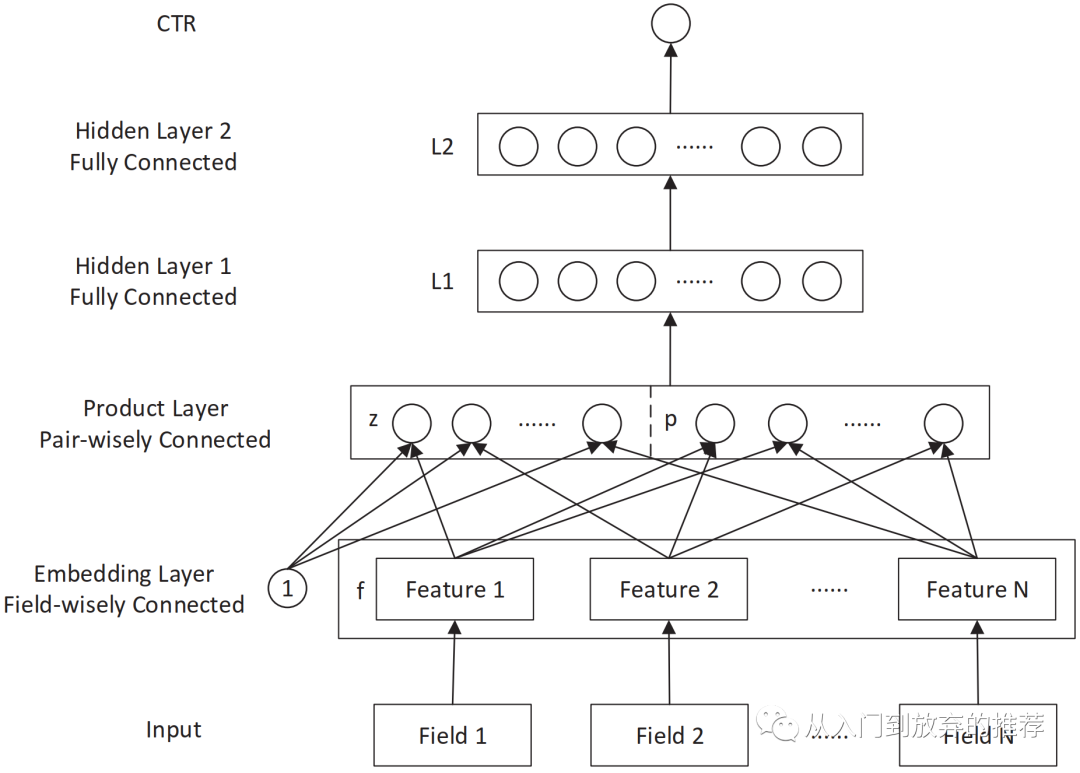
图6 PNN网络结构
6.2 embedding layer
利用embedding layer, PNN将原始高维稀疏特征转化为低维稠密特征作为模型的特征输入,如式子(22)所示,对第i个filed的特征,通过对应的参数
6.3 product layer
PNN的product layer包括线性和非线性两部分,通过这两部分对特征进行低阶交叉组合。在这一节中,论文中所使用的符号
6.3.1 线性部分
线性部分最终表征为
6.3.2 非线性部分
非线性部分指PNN的特征交叉部分,有两种操作方式,内积和外积,分别被称为IPPN和OPPN。非线性部分最终表征为
6.3.2.1 IPPN
当特征交叉使用内积方式时,
受矩阵分解的启发,对非线性部分的内积进行简化,将矩阵
def cross_layer_ipnn(params, input_layer):''':param params: the model config params:param input_layer: [B, F, K]:return: cross feature lp [B, D1]'''layer_name = 'cross_layers_pnn'field_size = input_layer.shape[1].value # return the F number input_layer [B, F, D]output_size = params.cross_layers['out_dim']kernel_initializer = tf.glorot_uniform_initializer()input_x = tf.transpose(input_layer, [0, 2, 1]) # [B, K, F]field_cross_fea = tf.matmul(input_layer, input_x) # ([B, F, K], [B, K, F]) -> [B, F, F] all feild crossfield_cross_fea = tf.reshape(field_cross_fea, [-1, field_size * field_size]) # [B, F, F] -> [B, F*F]comb_dim = field_cross_fea.shape[1].value # F*Foutput_w = tf.get_variable(name="{0}_nl_w".format(layer_name),shape=[comb_dim, output_size],dtype=tf.float32,initializer=kernel_initializer,) # [F*F, output_dim]# lp # [B, comb_dim], [comb_dim, output_dim] -> [B, output_dim]output_layer = tf.matmul(field_cross_fea,output_w,name="{0}_output".format(layer_name))return output_layer
6.3.2.2 OPPN
当特征交叉使用外积方式时,特征两两交叉的形式为
product layer通过线性部分和非线性部分对特征低阶进行了充分的交叉组合,再将两部分输出相加,作为dnn的输入,如式子(27)所示。
PNN的参数求解和普通的DNN相同。
PNN将FM和DNN的结合设计到end-to-end的网络结构中,不需要分阶段训练,实现方便。但PNN也存在一些不足:
(1) 特征交叉部分的内积和外积的计算复杂度高,虽然有近似处理,但会损失一些信息量;
(2) PNN虽然在product layer做了特征低阶的交叉和组合,但其结果作为DNN的输入,导致整个模型最终学到的是高阶的组合特征,忽略了低阶部分。
7 NFM
NFM[9] 出自论文《Neural Factorization Machines for Sparse Predictive Analytics》,发表于SIGIR2017。
NFM既保留了低阶特征的组合,又结合FM和DNN对特征进行高阶交叉,相比于FNN和PNN,它保留了低阶特征的信息。
NFM模型如式子(28)所示,形式和FM类似,不同的是对交叉特征项的处理,FM是直接对二阶交叉项求和,而NFM通过结合FM和DNN,通过网络结构学习特征之间的交叉性,即式子中的
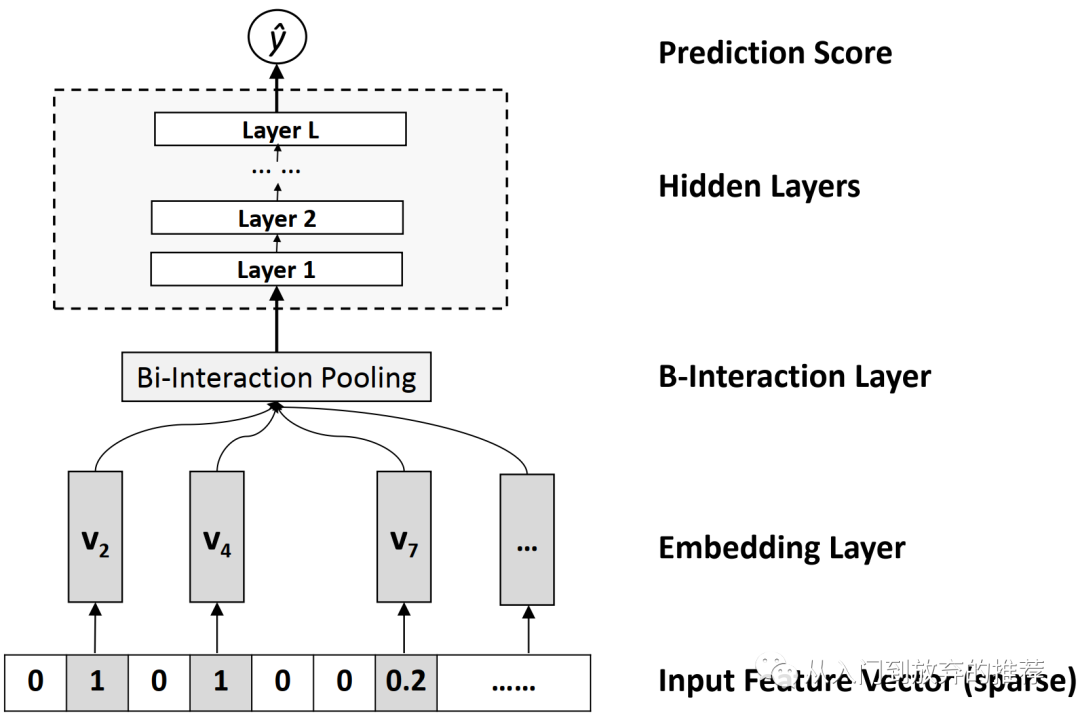
图7 NFM中特征交叉项f(x)的网络结构
网络的输入是高维稀疏的原始特征,通过embedding层,得到低维稠密的embedding表征
将DNN的计算放进NFM模型的式子,则可将其表示为式子(30)。当DNN只有一层,且
NFM的参数求解同普通的DNN。
NFM不仅考虑了低阶特征的组合信息,同时通过在网络结构中使用BI层对二阶交叉特征进行向量表征,保留了其信息量,提高了后续DNN对高阶特征交叉的能力。
8 DeepFM
DeepFM[10] 出自论文《DeepFM: A Factorization-Machine based Neural Network for CTR Prediction》,发表于IJCAI2017。
DeepFM和前面介绍的几种模型(FNN、PNN、NFM)类似,充分结合FM和DNN对特征交叉优势。不同的是,前面几种模型采用的是串行思路,将交叉后的特征作为DNN的输入,使得模型最终难以保留低阶特征交叉组合信息;而DeepFM采用了并行的思路,使得模型最终既保留了特征的低阶交叉组合信息,又具有高阶交叉信息,提高了模型的表征能力。DeepFM的模型设计思路类似Wide&Deep,将显式特征交叉和隐式特征交叉两部分结构并行化,这也是后续DCN系列模型的设计思路。
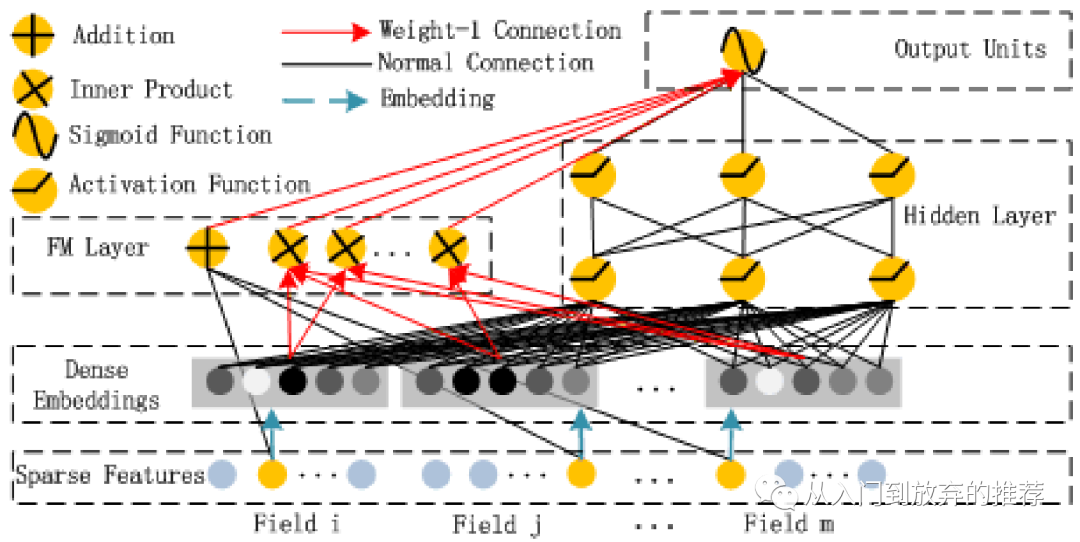
图8 DeepFM网络结构
DeepFM的网络结构如图8所示,通过dense embedding层将高维稀疏的原始特征转化为低维稠密embedding输入。左边部分为FM显式特征交叉结构,如图9所示,既包括一阶特征线性组合,也包括特征二阶交叉,如式子(31)所示。DeepFM网络结构右边部分为DNN结构,即对embedding输入进行高阶特征交叉。
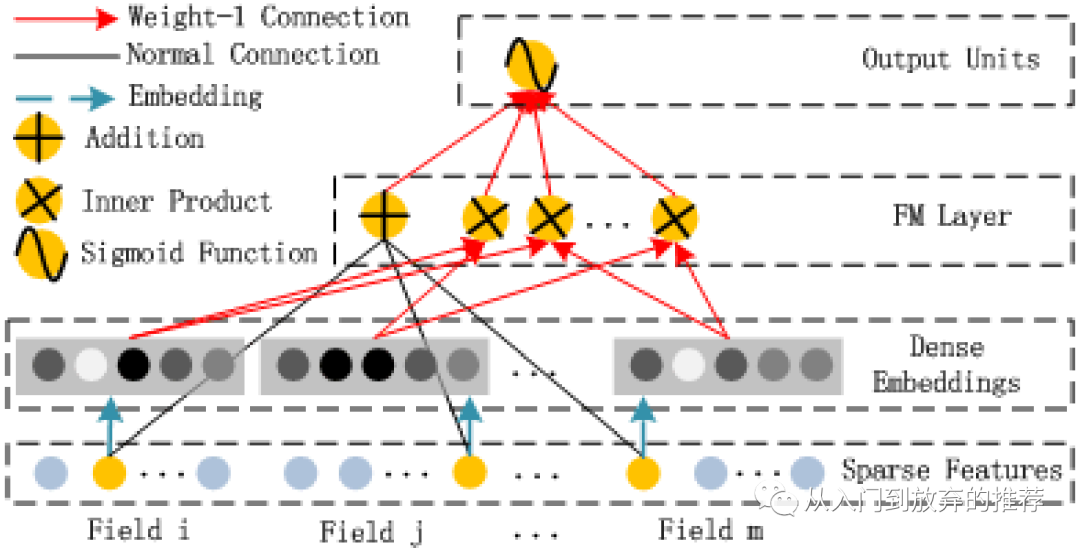
图9 FM网络结构
模型最后的输出如式子(32)所示,对FM部分和DNN部分加和后经过sigmoid得到结果。参数求解同一般的DNN。
代码2 DeepFM中FM的代码
def fm_layer(params, sparse_x, embedding_x, mode, layer_dropout=1):'''Reference: [IJCAI 2017] DeepFM: A Factorization-Machine based Neural Network for CTR Prediction:param params: the model config params:param sparse_x: raw feature input [B, N]:param embedding_x: dense feature embedding [B, F, K]:return: lr: [B, 1] , fm: [B, K]'''layer_name = 'fm_layer'kernel_initializer = tf.glorot_uniform_initializer()sparse_dim = sparse_x.shape[1].value # Nfm_layer_out = []# linear partif params.fm_layers['use_linear']:kernel = tf.get_variable(name="{0}_linear_w".format(layer_name),shape=[sparse_dim, 1],dtype=tf.float32,initializer=kernel_initializer,) # [N]linear_out = tf.matmul(sparse_x, kernel, name="{0}_linear_out".format(layer_name)) # [B, N], [N, 1] -> [B, 1]fm_layer_out.append(linear_out)# second orderembedding_input = embedding_x # [B, F, K]summed_features_emb = tf.reduce_sum(embedding_input, 1) # [B, K]summed_features_emb_square = tf.square(summed_features_emb) # [B, K]squared_features_emb = tf.square(embedding_input) # [B, F, K]squared_sum_features_emb = tf.reduce_sum(squared_features_emb, 1) # [B, K]fm_output = 0.5 * (tf.subtract(summed_features_emb_square, squared_sum_features_emb)) # [B, K]if layer_dropout < 1.0:fm_output = tf.layers.dropout(fm_output, rate=1 - layer_dropout, training=(mode == tf.estimator.ModeKeys.TRAIN))fm_layer_out.append(fm_output)output_layer = tf.concat(fm_layer_out, axis=1) # [B, 1+K]return output_layer
我在自己的业务场景对交叉特征进行改进时,发现一个细节问题,即交叉特征的表征方式不同,信息量的不等价问题。FM是对交叉特征进行求和,所以用优化算法和不用优化算法完全等价,而如果想表征成一个向量,后续再进行操作,则有一些差异。如论文中FM网络结构所示,是对域之间进行两两交叉,交叉的形式为内积,此时得到的向量表征的维度为
DeepFM通过网络结构的并行性,充分结合了FM和DNN对特征交叉的优势,相比同样网络结构并行化的Wide&Deep,它实现了特征的自动低阶交叉,不需要依赖人工设计。FM部分和DNN部分通过embedding共享,加速了网络的训练过程,且有利于embedding学得更充分。
DeepFM在业界取得了很好的效果,是一个不错的base。针对DeepFM在特征交叉上的提升空间,主要聚焦在特征交叉的高阶性问题。由于DNN的高阶交叉是隐式的,对工程师来说是一个黑盒状态,因此后续对其改进的思路是通过设计可以显式的高阶特征交叉网络结构,实现特征的高阶显式交叉,这也是后面DCN系列模型的思路,下一篇继续分享。
以及朋友们有什么想要一起探讨的,可以在评论区告诉我,共同学习一起进步呀~
相关面试问题
对FM模型的改进模型有那些
DeepFM的原理,FM和DNN在输出上是怎么结合的
reference
[5] Attentional Factorization Machines: Learning the Weight of Feature Interactions via Attention Networks
[6] Field-weighted Factorization Machines for Click-Through Rate Prediction in Display Advertising
[7] Deep Learning over Multi-field Categorical Data– A Case Study on User Response Prediction
[8] Product-based Neural Networks for User Response Prediction
[9] Neural Factorization Machines for Sparse Predictive Analytics
[10] DeepFM: A Factorization-Machine based Neural Network for CTR Prediction
推荐系列文章:
- 推荐模型结构-特征交叉
- 基础知识类
- 工具类
微信最近对公众号的推送算法改版较大,为了更好地找到我,动动手对这个公众号置顶呀~
公众号的内容会同时在知乎专栏更新,有兴趣的朋友可以在知乎找我玩,知乎专栏:
从入门到入门的推荐。
生活的思考和记录会在另一个公众号更新,有兴趣的朋友也可以动手关注一下






